卡尔曼滤波算法学习记录

关键节点：

协方差矩阵\(P_{k}\)：因为我们要利用速度与位置的某种关系来预测下一步位置，所以这个协方差矩阵表示的就是二者之间的相关性。简单来说，矩阵中的每个元素\(\sum\nolimits_{ij}\)表示第 i 个和第 j 个状态变量之间的相关度,协方差矩阵通常用\(\sum\nolimits_{}\) 来表示，其中的元素则表示为\(\sum\nolimits_{ij}\)。
最佳估计\(\hat{x}\):即均值，其它地方常用 μ 表示
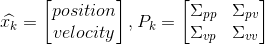
当前状态：k-1时刻
下一状态：k时刻
运动学公式：由运动学公式所列出来的式子可以看做状态转移矩阵
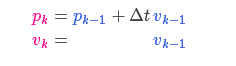
更新协方差矩阵：将分布中的每个点都乘以矩阵 A，得到下图
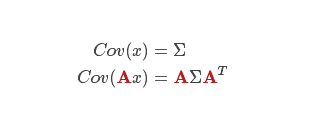
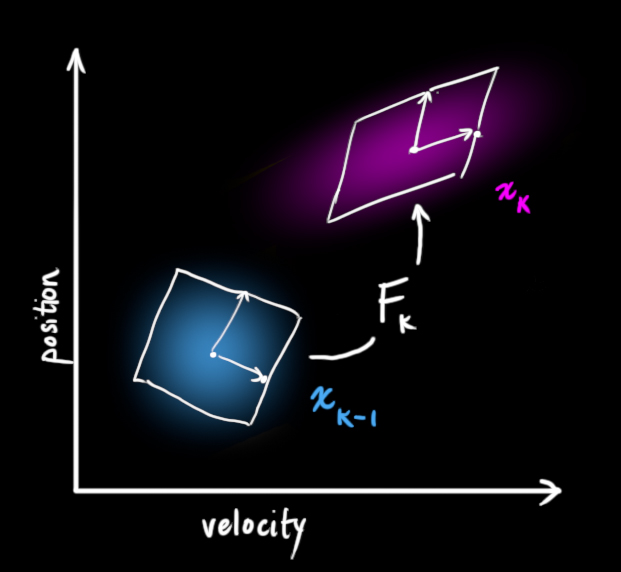
预测过程：状态转移矩阵\(F_{k}\)
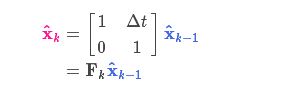
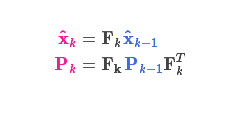
外部控制量：可能存在外部因素会对系统进行控制，带来一些与系统自身状态没有相关性的改变，（以火车的运动状态模型为例，火车司机可能会操纵油门，让火车加速），我们可以用一个向量\(\vec{x_k}\)来表示，将它加到我们的预测方程中做修正。我们知道了期望的加速度α，根据基本的运动学方程可以得到：

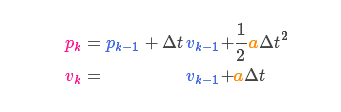
　　以矩阵的形式表示就是：

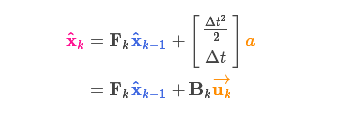
其中：\({B_k}\)称为控制矩阵，\(\vec{u_k}\)称为控制向量（对于没有外部控制的简单系统来说，这部分可以忽略）
外部干扰：一些系统之外的干扰，例如飞行器收到风力的干扰，机器人受到坡度的影响在每次预测之后，我们可以添加一些新的不确定性来建立这种与“外界”（即我们没有跟踪的干扰）之间的不确定性模型：

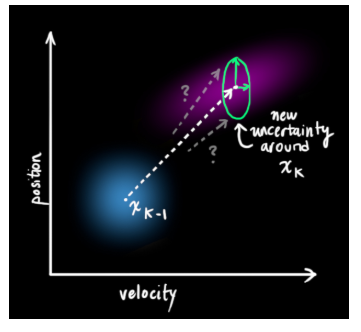
同时，原始估计中的每个状态变量更新到新的状态后，仍然服从高斯分布（包括我们之前没有特别去考虑的外部干扰）。我们可以说\({\hat{x}_{k-1}}\)的每个状态变量移动到了一个新的服从高斯分布的区域，协方差为\({Q_k}\)。换句话说就是，我们将这些没有被跟踪的干扰当作协方差为\({Q_k}\)的\(\color{red}{噪声}\)来处理。

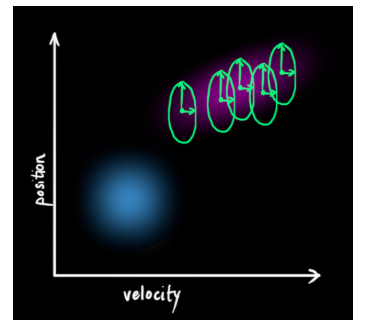
这产生了具有不同协方差（但是具有相同的均值）的新的高斯分布。

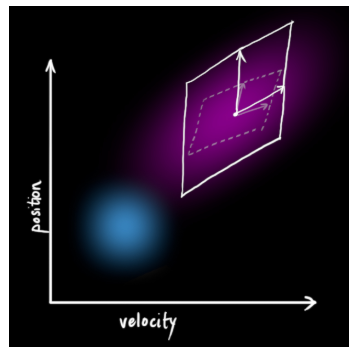
我们通过简单地添加\({Q_k}\)得到扩展的协方差，下面给出预测步骤的完整表达式：

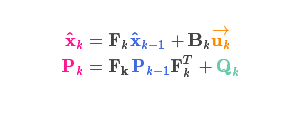
由上式可知，\(\color{#006600}{新的最优估计}\)是根据\(\color{#dd00dd}{上一最优估计}\)预测得到的，并加上\(\color{#660066}{已知外部控制量}\)的修正。
而\(\color{#006600}{新的不确定性}\)由\(\color{#dd00dd}{上一不确定性}\)预测得到，并加上\(\color{#DAA585}{外部环境的干扰}\)。
至此，我们对系统可能的动向有了一个模糊的估计，用这里\(\hat{X_k}\)和\({P_k}\)来表示,此时我们还没有考虑传感器所测量的数据。

用测量值来修正估计值
我们可能会有多个传感器来测量系统当前的状态，哪个传感器具体测量的是哪个状态变量并不重要，也许一个是测量位置，一个是测量速度，每个传感器间接地告诉了我们一些状态信息。
卡尔曼滤波包括两个部分：时间更新与测量更新，且是一个自回归过程
- 时间更新：滤波器使用上一状态的估计，作出对当前状态的估计

参考博客：
[详解卡尔曼滤波原理]（https://blog.csdn.net/u010720661/article/details/63253509）
[博客2]（https://www.cnblogs.com/rouwawa/p/11643850.html）
[博客3]（暂无）