图的逻辑结构：多对多。

图的存储结构：

数组表示法（邻接矩阵）

无向图的邻接矩阵

图没有顺序存储结构，但可以借助二维数组来表示元素之间的关系

数组表示法（邻接矩阵）：

无向图的邻接矩阵：

例：

共有5个顶点，所以形成5*5的方阵。

举个例子，比如第一行：

v1与v1本身之间无边，无邻接关系，所以为0

v1与v2之间有边，有邻接关系，所以为1

v1与v3之间无边，无邻接关系，所以为0

v1与v4之间有边，有邻接关系，所以为1

v1与v5之间无边，无邻接关系，所以为0

特点：

对角线上的元素都是0（因为对角线上都是每一个顶点到自身的边，是不存在的）

对称性：关于对角线对称（因为无向图中如果v1和v2之间有边，那v2和v1之间也有边）

由邻接矩阵可以得到：

顶点 i 的度=第 i 行（列）中1的个数

完全图的邻接矩阵中，对角线上元素为0，其余均为1

有向图的邻接矩阵：

如果是该顶点发出的到其它顶点的弧，那么它到其它顶点的值都记为1，反之记为0。

例：

举个例子，比如还是第1行：

v1没有发向v1自身的弧，所以为0

v1有发向v2的弧，所以为1

v1有发向v3的弧，所以为1

v1没有发向v4的弧，所以为0

特点：

有向图的邻接矩阵可能是不对称的

顶点的出度=第 i 行元素之和

顶点的入度=第 i 列元素之和

顶点的度=第 i 行元素之和+第 i 列元素之和

网（即有权图）的邻接矩阵：

例：

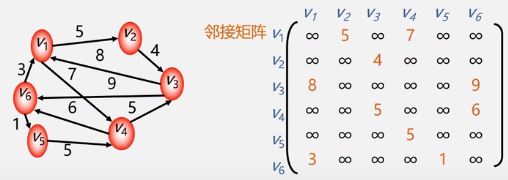
同样以第一行为例：

v1没有发向v1自身的弧，所以记为无穷

v1有发向v2的弧，且权值为5，所以记为5

v1没有发向v3的弧，所以记为无穷

v1有发向v4的弧，且权值为7，所以记为7

v1没有发向v4的弧，所以记为无穷

v1没有发向v4的弧，所以记为无穷

用邻接矩阵来建立无向网：

定义：

算法思想：

算法：

示例代码：

代码实现：

#include<iostream>
using namespace std;
#define OK 1
#define Maxint 32767//表无穷，一个很大的数 
#define MVNum 100//表最大顶点数 
typedef char VerTexType;//设顶点类型为字符型 
typedef int ArcType;//假设边的权值类型为整型 
typedef int Status; 
//
typedef struct
{
	VerTexType vexs[MVNum];//顶点表 
	ArcType arcs[MVNum][MVNum];//邻接矩阵 
	int vexnum,arcnum; //图的当前顶点数和边数 
}AMGraph;
Status CreateUDN(AMGraph &G);//建立无向网 
int LocateVex(AMGraph G,VerTexType u);//查找该字符在顶点表中的下标 
int main() 
{
	AMGraph G;
	//函数调用 
	CreateUDN(G);
	return 0;
}
//建立无向网 
Status CreateUDN(AMGraph &G)
{
	cin>>G.vexnum>>G.arcnum;//输入总顶点数和总边数 
	int i,j,k,w;
	char v1,v2;
	for(i=0;i<G.vexnum;i++)
	{
		cin>>G.vexs[i];//输入顶点 
	}
	for(i=0;i<G.vexnum;i++)
	{
    	for(j=0;j<G.vexnum;j++)
    	{
    		G.arcs[i][j]=Maxint;//将邻接矩阵初始化为最大值 
		}
    }
    for(k=0;k<G.arcnum;k++)
    {
    	cin>>v1>>v2>>w;
    	//查找 
    	i=LocateVex(G,v1);
    	j=LocateVex(G,v2);
    	G.arcs[i][j]=w;
    	G.arcs[j][i]=G.arcs[i][j];//对称 
	}
	cout<<"输出邻接矩阵:"<<endl;
	for(i=0;i<G.vexnum;i++)
	{
		for(j=0;j<G.vexnum;j++)
		{
			cout<<G.arcs[i][j]<<" ";
		}
		cout<<endl;
	}
}
//查找该字符在顶点表中的下标  
int LocateVex(AMGraph G,VerTexType u)
{
	int i;
	for(i=0;i<G.vexnum;i++)
	{
		if(u==G.vexs[i])
		return i;
	}
		return -1;
}

运行结果：