卷积总结
在以一个像素为中心的邻域中计算线性算子。可以被认为是在图像上滑动一个固定系数的核，同时在重叠部分进行一个加权和。
注意：
满：在核和图像之间计算任何重叠部分的值（产生的图像比原图像大）
相同：仅在核的中心像素与图像中的像素对齐时才计算值
卷积：在图像上滑动之前，核旋转180度
互相关：核不会首先被旋转
边界处理方法：定义图像以外的值
问题：导数与噪声
问题：导数与噪声
噪声影响一阶导数
数值导数可以放大噪声！（特别是高阶导数）
图像噪声
事实：图像是有噪声的
我们对图像中的噪声并不感兴趣
例子：光照波动，传感器噪声，量化效应，有限精度
图像噪声建模
简单的模型：加性的随机噪声
I(x,y) = s(x,y) + ni
其中s(x,y)是确定性的信号，ni是一个随机变量
常见假设：
对所有像素而言n是独立同分布的
n是零均值高斯（正态）分布
E(n) = 0 var(n) = σ2
E(ni nj) = 0 (独立性)
注意：这确实只模拟传感器噪声。
例子：添加的高斯噪声
实际证明
其他噪声模型
我们不会涉及这些。但需要知道他们存在！
乘性噪声：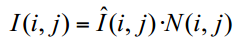
脉冲 (“短”)噪声 (又名椒盐噪声)
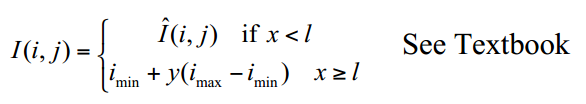
平滑操作减小噪声
数据平滑的前提是测量一个既缓慢变化又被随机噪声污染的变量。有时用周围数据点的某种局部平均值替换每个数据点是有用的。由于附近的点测量的基本值非常接近，平均值可以降低噪声水平并且不会（很大程度上）偏移所获得的值。
当前：平滑减小噪声
平滑减小噪声，（可能）提供给我们一个更准确的灰度曲面
预览
我们将探讨两种平滑滤波器
盒式滤波器（简单的平均化）
高斯滤波器（中心像素加权更多）
平均/盒式滤波器
值为正的元素总和为1的mask
将每个像素替换为其邻域的平均值
由于所有的权值都相等，所以被称为盒式滤波器
重点：由于这是一个线性算子，所以我们可以通过用图像与这个3*3滤波器卷积来获得每个像素周围的平均值
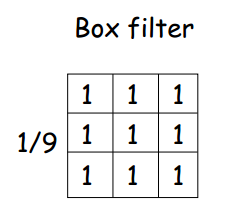
为什么平均化减小噪声
直观的解释：在平均值中的噪声方差小于像素噪声方差（假设为零均值高斯噪声）
更严谨的表述：
盒式滤波器平滑
缺点：平滑减小精细图像细节
平滑的重点
平均值可以衰减噪声（减少方差），从而得到更“精确”的估计值。
然而，更精确的估计是一个局部像素邻域的平均值。这可能不是你们想要的。
平衡操作：平滑到足够可以去掉噪声，但同时不足以去除重要的图像梯度
高斯平滑滤波器
加权平均的一个例子
—系数是二维高斯分布
—在中心像素处赋予更多权重，而在相邻像素处赋予更少权重
—离中心越远，权重越小
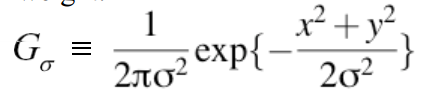
易混淆点：现在这里讨论两个高斯（一个用于噪声，一个用于平滑）。它们是不同的。
各向同性（圆对称）高斯
Matlab
注意：这里我们没有包含标准化常数（高斯分布的系数）。高斯分布的值加起来需要为1。然而由于之后你会除以这个值，这里忽略掉这个常数就没关系。
高斯平滑滤波
只是另一个线性滤波器。执行加权平均。
能够和图像进行卷积产生一个更平滑的图像
高斯平滑例子
盒式vs高斯
高斯是一个真正的低通滤波器，所以不会引起高频伪影
在不同尺度的高斯平滑
在本课程的后面，我们将更深入地探讨尺度和分辨率的概念。
小小的离题…
你能猜出我在卷积时用了什么边界处理方法吗？
实现问题
一个高斯mask应该多大？
—高斯的标准差σ 决定了平滑的量
—高斯理论上是无限的数量，但我们需要一个有限尺寸的滤波器
—针对98.76% 的区域，我们需要+/-2.5σ
—+/- 3σ覆盖了超过99%的区域
高效的实现
盒式滤波器和高斯滤波器都是可分离的：
—首先用一个一维滤波器卷积每一行
—接着用一个一维滤波器卷积每一列
可分离的高斯：可结合性
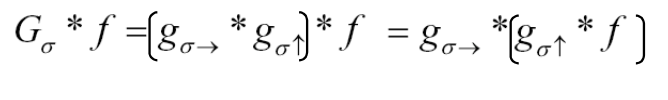
高效的实现
级联高斯
—较小的高斯重复卷积模拟较大高斯的效应
G*(Gf) = (GG)*f （结合律）
非常重要：
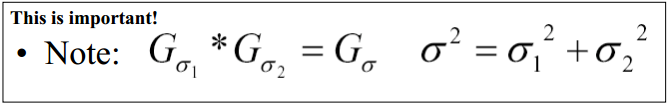
空间域的卷积是频域的乘法（傅里叶空间）
高斯的傅里叶变换：
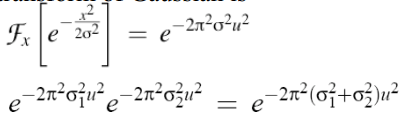
易混淆点： σ为标准差，σ2是方差
回忆：导数和噪声
导数算子受噪声影响
数值导数会放大噪声！（特别是高阶导数）
解决方法：应用导数算子之前进行平滑
问题：我们必须在这里应用两个线性运算（卷积）吗？
如同这样两个线性运算
平滑和微分
不，我们可以把两个滤波器结合起来！
通过卷积算子的结合性质：
(导数滤波器 * 平滑滤波器 )：我们可以将这个部分作为一个单独的核进行预计算
例子：Prewitt算子
卷积计算：
这个mask被称为（垂直的）Prewitt边缘检测器
例子：Prewitt算子
卷及计算：
这个mask被称为（水平的）Prewitt边缘检测器
例子：Sobel算子
卷积计算：
赋予四个邻域值更大的权重
重要的发现
注意，Prewitt算子是一个与导数算子卷积的盒式滤波器 [使用“满”选项]。
同样注意：Sobel算子是一个与导数算子卷积的 [1 2 1] 滤波器
推广：平滑导数
解决方法：首先通过高斯滤波Gs平滑图像，然后求导：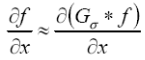
应用卷积的微分性质：
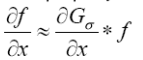
因此，图像x处的求导能够通过和高斯滤波的导数进行卷积实现：
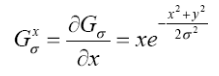
重要性质：高斯导数也是可分离的：
高斯的一阶（偏）导数
作为一个mask，这也是计算一个差分（导数）
和有限差分算子比较
高斯滤波器的导数
总结：平滑导数
