计算机视觉(图像拼接总结4)yg/?

前言

什么,已经到第四步了么...总之第四步是什么来着?我想想....啊,没错,是求解线性变换方程组,这可是个大工程!

正文

理论

这里大概要先说一下超级多的变换了吧:

好,了解了这些变换,我们之后的求解线性变换方程组就可以开始了.

首先我们要明确一点两张图像可拼接的前提条件是其上面所有的点都满足射影变换 ,实际上在一般情况下,对同一个平面的点拍照得到的两张不同照片,都满足射影变换,但是如果被拍摄的点不全在一个平面上,则两张照片不满足射影变换,如下图:

在这个示意图里,c是相机,矩形就是照片

然后这边还要介绍一下齐次坐标的相关知识:

齐次坐标（Homogeneous Coordinates）是计算机图形学和计算机视觉领域中的一个重要概念。它是在三维空间中表示点和向量的一种方法，通常用四个坐标值（x, y, z, w）来表示一个点或一个向量。这里，x、y、z表示三维坐标值，w通常被设置为1。

齐次坐标的主要优势在于它可以将平移、旋转、缩放等线性变换统一表示为矩阵乘法。这种统一性使得在计算机图形学和计算机视觉中处理各种变换操作更加方便和高效。齐次坐标的矩阵表示通常是一个4x4的矩阵。

下面是一个简单的示例，说明了齐次坐标在矩阵中的使用。假设有一个三维点P(x, y, z)，它的齐次坐标表示为P(x, y, z, 1)。现在，我们想要对这个点进行平移操作，将其在x、y、z方向上分别平移Tx、Ty、Tz个单位。

平移操作的齐次坐标矩阵表示为：

```
| 1  0  0  Tx |
| 0  1  0  Ty |
| 0  0  1  Tz |
| 0  0  0  1  |
```

如果我们将点P的齐次坐标表示为列向量[Px, Py, Pz, 1]，平移矩阵表示为上述的4x4矩阵，那么点P'（平移后的点）的齐次坐标可以通过以下矩阵乘法计算得到：

```
| Px' |     | 1  0  0  Tx |   | Px |
| Py' |  =  | 0  1  0  Ty | * | Py |
| Pz' |     | 0  0  1  Tz |   | Pz |
|  1  |     | 0  0  0  1  |   |  1 |
```

得到的结果是一个齐次坐标[Px', Py', Pz', 1]，如果我们将最后的1舍去，就得到了平移后的三维点P'(Px', Py', Pz')。这样，无论是平移、旋转还是其他线性变换，都可以通过构造对应的齐次坐标矩阵来实现，使得各种变换操作更加简洁和高效。

接下来就是相关的实现了:

这是一个典型的坐标射影变换,这里的c其实无关紧要,因为在其次化中都会一样,然后可以将这个式子化作为;

然后将这个式子转化成:

这个时候我们就可以开始解这个方程了,首先我们可能需要了解一下,什么情况下这种方程组有解:

这里的话,因为矩阵 A可能不是 n×n 的矩阵，而是 m×n 的矩阵（其中 m 表示方程组的数量，n 表示未知数的数量），线性方程组的解的情况会有所不同。

1. **方程组个数少于未知数个数（m < n）：** 当方程组的数量少于未知数的数量时，通常会存在无穷多解。这是因为方程组的个数不足以约束所有的未知数，所以存在自由变量，可以取不同的值得到不同的解。

2. **方程组个数等于未知数个数（m = n）：** 当方程组的数量等于未知数的数量时，可以有三种情况：
   - 如果系数矩阵 A 是满秩的（即所有行都线性独立），那么方程组有唯一解。
   - 如果系数矩阵 A 不是满秩的，但是常数向量 b 在系数矩阵的列空间内（即 b 可以由 A 的列向量线性表示），那么方程组有无穷多解。
   - 如果系数矩阵 A 不是满秩的，并且常数向量 b 不在系数矩阵的列空间内，那么方程组无解。

3. **方程组个数大于未知数个数（m > n）：** 当方程组的数量多于未知数的数量时，通常会存在无解。这是因为方程组的个数过多，无法满足所有的方程，导致矛盾。

显然这里的情况是会得到无解

要注意的是，当求 A 2n*9 *h 9*1 =0 2n*1 时(一般不这样做)，为了防止解出来的 h=0，我们会人为加上一个条件||h||=1，于是上述方程就变成了一个 带约束条件的求一个函数的极 值点解 ，这个时候你要用到 拉格朗日乘子法 ：

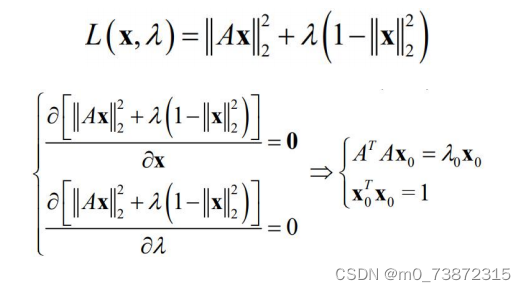
首先介绍一下吧:"

拉格朗日乘子法（Lagrange Multiplier Method）是一种用于求解带有约束条件的优化问题的数学技术。它是基于拉格朗日定理的，该定理指出，在满足一定条件的情况下，一个多变量函数在其约束条件下的极值点可以通过构造一个带有拉格朗日乘子的增广拉格朗日函数来找到。拉普拉斯乘子法是拉格朗日乘子法在概率和统计学中的应用，用于求解多元函数的条件极值问题。

"回到我们的问题,实际上就是使用这个方程不断地求偏导得到最终的驻点即可.

要注意到的是，不论是解 A 2n*8 *h 8*1 =b 2n*1 还是解 A 2n*9 *h 9*1 =0，n 都至少是 4，因为当 n 刚好等于 4 时，h 有一个线性无关的解，当 n 大于 4 时，解 h 就要用到线性最小二乘 法了。为什么 n 一定要为 4？正统地，是线性代数的知识；不正统地，h 有 8 个自由度，A 的每个行构成一个线性方程，消除一个自由度。

这里附加上对矩阵求偏导的一些小tips:

行向量不能对行向量求导，求导的结果的形状取决于微元的形状。标量对行向量求

导得到行向量，列向量对行向量求导得到矩阵

代码

简单演示

import cv2
import numpy as np

# 创建一个输入图像
input_image = np.zeros((300, 300), dtype=np.uint8)
input_image[50:250, 50:250] = 255  # 在图像中间创建一个白色方块

# 定义平移和旋转参数
tx, ty = 50, 50  # 平移参数
angle = 45       # 旋转角度

# 构造平移矩阵
translation_matrix = np.array([[1, 0, tx],
                               [0, 1, ty]], dtype=np.float32)

# 构造旋转矩阵
rotation_matrix = cv2.getRotationMatrix2D((input_image.shape[1] // 2, input_image.shape[0] // 2), angle, 1)

# 进行仿射变换
translated_image = cv2.warpAffine(input_image, translation_matrix, (input_image.shape[1], input_image.shape[0]))
rotated_image = cv2.warpAffine(input_image, rotation_matrix, (input_image.shape[1], input_image.shape[0]))

# 将变换后的图像拼接在一起
result_image = np.hstack((input_image, translated_image, rotated_image))

# 显示结果图像
cv2.imshow('Result Image', result_image)
cv2.waitKey(0)
cv2.destroyAllWindows()

结语

呱,总之结束了