图(一)-数据结构学习笔记

1. 图简介

1.1 图的分类

图分为

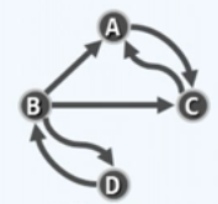
• 有向图 (digraph): 即所有边皆有向的图
  
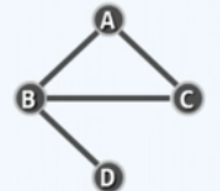
• 无向图 (undigraph): 即所有边皆无向的图
  
• 混合图(mixed graph): 即含有无向以及有向边的图
  
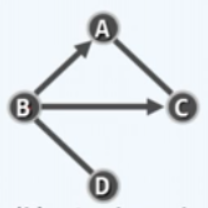
  虽然图分为上面三种, 但是我们重点分析有向图, 因为所有的图都可以由有向图简化得到

1.2 图的描述

基于任意一个图都可以由点集V 与边集 E组成 , 我们可以对图 G 做出如下描述

$G = (V;E)$

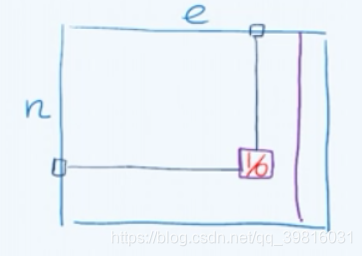
• V(vertex): V 代表图的点集, 我们令 $n = |V|$ ,n代表顶点的个数
• E(edge): E 代表图的边集, 我们令 $e = |E|$, e代表边的个数

1.2.1 边的描述

我们使用 $(u,v)$来描述一条边

• 若u,v的次序无所谓, 则称为 无向边(undirected edge), 容易看出,所有边均无方向即为无向图
• 若u,v的次序需要考虑,则(u,v)称为有向边(directed edge)
  • u为边 $(u,v)$的尾(tail)
  • v为边 $(u,v)$的头(head)

1.2.2 路径(path)/环路(circle)

路径描述

所谓路径, 就是我们所说的路径, 它由有向边构成, 所以我们可以做出如下的数学描述, 一条路径可以由k个顶点的有序序列描述 , $v_0$ 为路径的起点, $v_k$为路径的终点
$路径\pi = <v_0, v_1, ...,v_k>\\ 长度|\pi| = k$

路径分类

• path:
  • simple path:即没有重复节点的路径, 即不存在 i j , 使得 $v_i = v_j$
  • circle(环路): 即 $v_0 = v_k$,起点与终点相同的路径
    • simple circle: 即不包含重复节点的circle环路
  • DAG(有向无环图): 有向但是不存在环路的图 , 称为有向无环图
  • Hamiltonian tour(哈密尔顿环路): 每个顶点经过且只经过一次的环路, 称为哈密尔顿环路
  • Eulerian tour(欧拉环路): 覆盖了所有的边,经过每一个边一次且只经过一次的环路, 称为欧拉环路

2. 如何使用代码描述图

与一般的线性结构,树型结构不同, 图由边和顶点组成, 那么计算机中如何使用代码描述图呢?

2.1 邻接矩阵(adjacency matrix)和关联矩阵()

描述图一般有两种方式

• 邻接矩阵
• 关联矩阵

2.1.1 邻接矩阵

邻接矩阵就是利用矩阵元素间关系来描述顶点关系的一种方式
行为所有的顶点, 列也为所有的顶点
若 $(i,j)$位置的元素为1,则表示第 $i$个顶点为起点, 第j个顶点为终点的边

	A	B	C	D
A		1	1
B				1
C				1
D

例如上面的矩阵, 代表的图如下

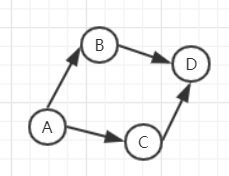
2.1.2 关联矩阵(incidence matrix)

在关联矩阵中,** 行代表顶点 , 列 代表边** , 矩阵中元素的值表明某一顶点与某一边是否有关联

注意因为一条边最多与两个节点关联, 因此如果1表示有关, 0表示无关,关联矩阵中 的列(边)最多有两个1,其他均为0