数论——快速幂剖析

快速幂，二进制取幂（Binary Exponentiation，也称平方法），是一个在 Ο(logn) 的时间内计算的小技巧，而暴力的计算需要 O(n) 的时间。

而这个技巧也常常用在非计算的场景，因为它可以应用在任何具有结合律的运算中。其中显然的是它可以应用于模意义下取幂、矩阵幂等运算，我们接下来会讨论。

一般快速幂递归方法实现

long long binpow(long long a, long long b) {
  if (b == 0) return 1;
  long long res = binpow(a, b / 2);
  if (b % 2)
    return res * res * a;
  else
    return res * res;
}

非递归方法实现

long long binpow(long long a, long long b) {
  long long res = 1;
  while (b > 0) {
    if (b & 1) res = res * a;
    a = a * a;
    b >>= 1;
  }
  return res;
}

问题1：快速幂取模

因为模运算对乘法无影响，代码实现如下

long long binpow(long long a, long long b, long long m) {
  a %= m;
  long long res = 1;
  while (b > 0) {
    if (b & 1) res = res * a % m;
    a = a * a % m;
    b >>= 1;
  }
  return res;
}

注意：根据费马小定理，如果 m 是一个质数，我们可以计算 x^n%(m-1)来加速算法过程。

问题2：矩阵快速幂

模板

struct Mat
{
    LL m[101][101];
};//存储结构体
Mat a,e; //a是输入的矩阵，e是输出的矩阵
Mat Mul(Mat x,Mat y)
{
    Mat c;
    for(int i=1;i<=n;++i){
        for(int j=1;j<=n;++j){
            c.m[i][j] = 0;
        }
    }
    for(int i=1;i<=n;++i){
        for(int j=1;j<=n;++j){
            for(int k=1;k<=n;++k){
                c.m[i][j] = c.m[i][j]%mod + x.m[i][k]*y.m[k][j]%mod;
            }
        }
    }
    return c;
}
Mat pow(Mat x,LL y)//矩阵快速幂
{
    Mat ans = e;
    while(y){
        if(y&1) ans = Mul(ans,x);
        x = Mul(x,x);
        y>>=1;
    }
    return ans;
}

1.斐波那契数列

斐波那契数列的递推可以用矩阵乘法的形式表达

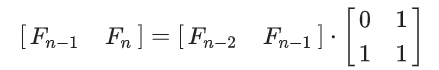
于是我们可以用矩阵乘法在 O(logn)的时间内计算斐波那契数列。此外，前一节讲述的公式也可通过矩阵对角化的技巧来得到。

2.定长路径计算

给一个有向图（边权为 1），求任意两点u，v 间从 u 到 v ，长度为k 的路径的条数。

我们把该图的邻接矩阵 M 取 k 次幂，那么 M_ij就表示从 i到 j长度为 k的路径的数目。该算法的复杂度是 O(n³logk)。

3.加速几何中对点集的操作

让我们来观察一下这三种操作对坐标的影响：

Shift 操作：将每一维的坐标分别加上一个常量；
Scale 操作：把每一维坐标分别乘上一个常量；
Rotate 操作：这个有点复杂，我们不打算深入探究，不过我们仍然可以使用一个线性组合来表示新的坐标。

可以看到，每一个变换可以被表示为对坐标的线性运算，因此，一个变换可以用一个4X4 的矩阵来表示：

现在，每一种操作都被表示为了一个矩阵，变换序列可以用矩阵的乘积来表示，而一个 Loop 操作相当于取一个矩阵的 k 次幂。

这样可以用 O(mlog(k))计算出整个变换序列最终形成的矩阵。最后将它应用到 n个点上，总复杂度 O(m+mlog(k)) 。

问题3：高精度快速幂

题目：从文件中输入 P（1000<P<3100000），计算的最后 100 位数字（用十进制高精度数表示），不足 100 位时高位补 0。

#include <bits/stdc++.h>
using namespace std;
int a[505], b[505], t[505], i, j;
int mult(int x[], int y[])  // 高精度乘法
{
  memset(t, 0, sizeof(t));
  for (i = 1; i <= x[0]; i++) {
    for (j = 1; j <= y[0]; j++) {
      if (i + j - 1 > 100) continue;
      t[i + j - 1] += x[i] * y[j];
      t[i + j] += t[i + j - 1] / 10;
      t[i + j - 1] %= 10;
      t[0] = i + j;
    }
  }
  memcpy(b, t, sizeof(b));
}
void ksm(int p)  // 快速幂
{
  if (p == 1) {
    memcpy(b, a, sizeof(b));
    return;
  }
  ksm(p / 2);
  mult(b, b);
  if (p % 2 == 1) mult(b, a);
}
int main() {
  int p;
  scanf("%d", &p);
  a[0] = 1;
  a[1] = 2;
  b[0] = 1;
  b[1] = 1;
  ksm(p);
  for (i = 100; i >= 1; i--) {
    if (i == 1) {
      printf("%d\n", b[i] - 1);
    } else
      printf("%d", b[i]);
  }
}

模意义下大整数乘法

也就是快速乘，思路如下

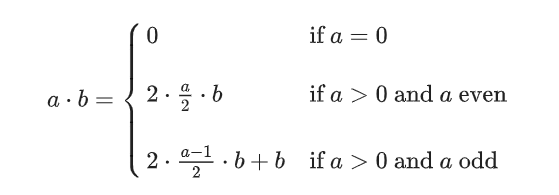
注意：也可以利用双精度浮点数在常数时间内计算大整数乘法。因为

快速乘代码实现

ll mul(ll a,ll b,ll p)
{
    ll ans=0;
    for(;b;b>>=1)
    {
        if(b&1)
            ans=(ans+a)%p;
        a=a*2%p;
    }
    return ans;
}

双精度代码实现

ll mul(ll a,ll b,ll p)
{
    a%=p;
    b%=p;
    ll c=(long double)a*b/p;
    ll ans=a*b-c*p;
    if(ans<0)
        ans+=p;
    else if(ans>=p)
        ans-=p;
    return ans;
}

数论——快速幂剖析

猜你喜欢