Mahony姿态解算算法笔记

Mahony姿态解算算法分析

mahony 算法是常见的姿态融合算法，将加速度计，磁力计，陀螺仪共九轴数据，融合解算出机体四元数，该算法可到其网站下载源码https://x-io.co.uk/open-source-imu-and-ahrs-algorithms/

该篇仅介绍融合加速度计和陀螺仪的六轴数据算法

1 空间姿态的常规描述

首先，姿态解算中的姿态实际上值得是机体坐标系与地理坐标系的位置关系。其常用描述形式有三种：欧拉角，方向余弦矩阵，四元数。

1.1 欧拉角

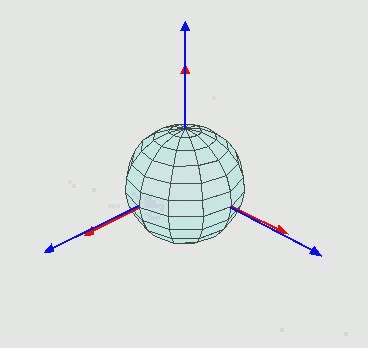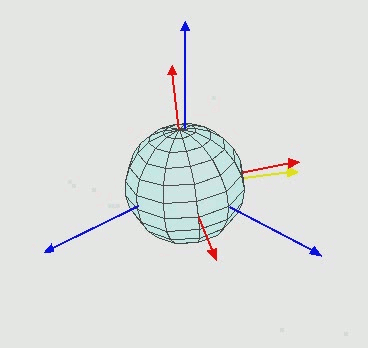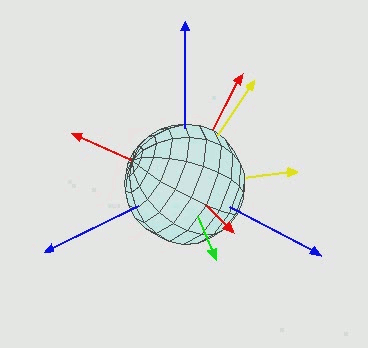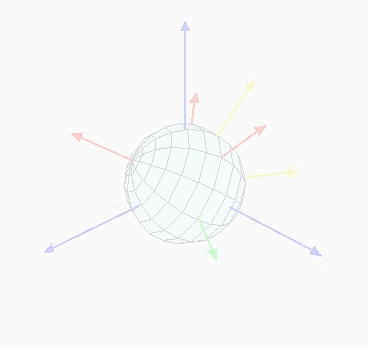
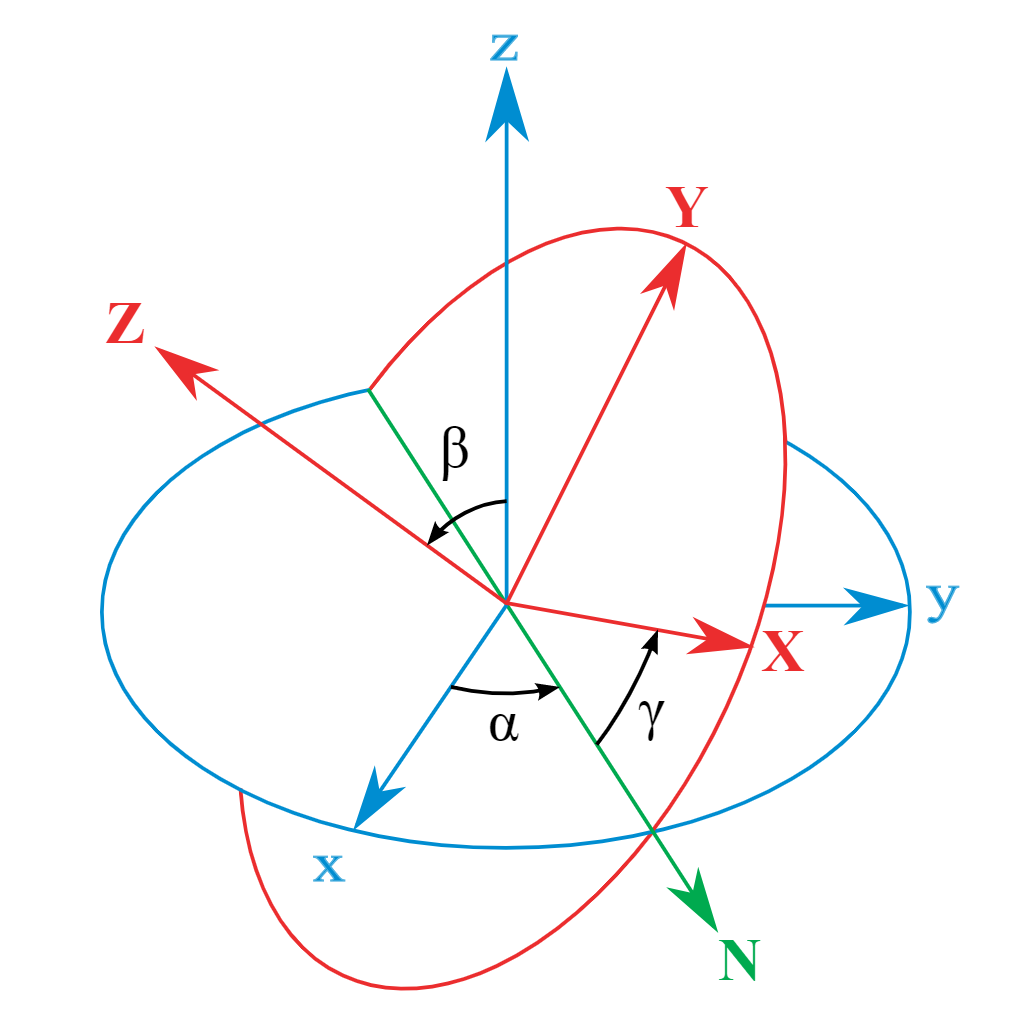
对于任何参考系，一个刚体的取向（也就是姿态解算中的姿态）可以围绕刚体坐标系以z-x-z轴顺序做三个欧拉角旋转而得出的。另外的，刚体的取向可以用三个基本旋转矩阵来确定，而将三个矩阵相乘可复合得到对于任何刚体旋转的旋转矩阵R，此处省略推导过程有兴趣的话可以自行谷歌。
\[ [\mathbf{R}]=\left[\begin{array}{ccc} {\cos \gamma} & {\sin \gamma} & {0} \\ {-\sin \gamma} & {\cos \gamma} & {0} \\ {0} & {0} & {1} \end{array}\right]\left[\begin{array}{ccc} {1} & {0} & {0} \\ {0} & {\cos \beta} & {\sin \beta} \\ {0} & {-\sin \beta} & {\cos \beta} \end{array}\right]\left[\begin{array}{ccc} {\cos \alpha} & {\sin \alpha} & {0} \\ {-\sin \alpha} & {\cos \alpha} & {0} \\ {0} & {0} & {1} \end{array}\right]\\ =\left[\begin{array}{ccc} {\cos \alpha \cos \gamma-\cos \beta \sin \alpha \sin \gamma} & {\sin \alpha \cos \gamma+\cos \beta \cos \alpha \sin \gamma} & {\sin \beta \sin \gamma} \\ {-\cos \alpha \sin \gamma-\cos \beta \sin \alpha \cos \gamma} & {-\sin \alpha \sin \gamma+\cos \beta \cos \alpha \cos \gamma} & {\sin \beta \cos \gamma} \\ {\sin \beta \sin \alpha} & {-\sin \beta \cos \alpha} & {\cos \beta} \end{array}\right] \]
欧拉角描述空间姿态的一大优点就是方式直观容易理解。但其存在的问题也很严重，即万向节死锁，网上有许多资料这里就不再赘述。

1.2 方向余弦矩阵

在经典欧拉角中我们围绕刚体坐标轴以z-x-z轴顺序旋转进而推导出一种空间中坐标转换矩阵，若围绕地理坐标系中的坐标轴旋转则可推导出以下绕三个坐标轴的旋转矩阵，与欧拉角复合三个矩阵的方式相同，我们将三个矩阵相乘即可得到方向余弦矩阵C。
\[ C_{1}^{}=\left[\begin{array}{ccc} {1} & {0} & {0} \\ {0} & {\cos \theta} & {\sin \theta} \\ {0} & {-\sin \theta} & {\cos \theta} \end{array}\right] \begin{array}{l} {C_{2}^{}=\left[\begin{array}{ccc} {\cos \gamma} & {0} & {-\sin \gamma} \\ {0} & {1} & {0} \\ {\sin \gamma} & {0} & {\cos \gamma} \end{array}\right]} \end{array} C_{3}^{}=\left[\begin{array}{ccc} {\cos \psi} & {-\sin \psi} & {0} \\ {\sin \psi} & {\cos \psi} & {0} \\ {0} & {0} & {1} \end{array}\right] \]

\[ C_{}^{}=C_1C_{2}C_{3}\\ C_{}^{}=\left[\begin{array}{ccc} {\cos \gamma \cos \psi+\sin \gamma \sin \psi \sin \theta} & {\sin \gamma \cos \psi \sin \theta-\cos \gamma \sin \psi} & {-\sin \gamma \cos \theta} \\ {\sin \psi \cos \theta} & {\cos \psi \cos \theta} & {\sin \theta} \\ {\sin \gamma \cos \psi-\cos \gamma \sin \psi \sin \theta} & {-\cos \gamma \cos \psi \sin \theta-\sin \gamma \sin \psi} & {\cos \gamma \cos \theta} \end{array}\right] \]

上述表示方法虽然直观，但其在公式中存在大量的三角函数式，而大量的三角函数会显著延长运算时间导致控制周期变长进而影响控制效果。因此，我们需要另一种方便计算的描述方式——四元数

1.3 四元数

四元数的定义与复数非常类似，唯一的区别是复数只有一个虚部，而四元数一共有三个。所有的四元数 q ∈ H
（H代表四元数的发现者William Rowan Hamilton）都可以写成下面这种形式：
\[ q=a+b i+c j+d k \quad(a, b, c, d \in \mathbb{R})\\ 或\\ q=q_{0}^{}+q_{1}^{} i+q_{2}^{} j+q_{3}^{} k \quad(q_{0}^{}, q_{1}^{}, q_{2}^{}, q_{3}^{} \in \mathbb{R}) \]
其中：
\[ i^{2}=j^{2}=k^{2}=i j k=-1 \]
与复数类似，四元数就是基{1，i，j，k}的线性组合，同样的，四元数也可以写成向量形式：
\[ q=\left[\begin{array}{l} {q_{0}^{}} \\ {q_{1}^{}} \\ {q_{2}^{}} \\ {q_{3}^{}} \end{array}\right] \]
另外的，我们也可以将实部与虚部分开，即通过一个三维向量表示虚部，从而将四元数表示为标量与向量的有序对形式：
\[ q=[s, \mathbf{v}] \quad\left(\mathbf{v}=\left[\begin{array}{l} {x} \\ {y} \\ {z} \end{array}\right], s, x, y, z \in \mathbb{R}\right) \]

1.3.1.1 模长

仿照复数的定义，我们可以将一个四元数 \(q = a + bi + cj + dk\) 的模长定义为：
\[ \|q\|=\sqrt{a^{2}+b^{2}+c^{2}+d^{2}} \]
如果用有序对形式表示的话：
\[ \begin{aligned} \|q\| &=\sqrt{s^{2}+\|\mathbf{v}\|^{2}} \\ &=\sqrt{s^{2}+\mathbf{v} \cdot \mathbf{v}} \end{aligned} \]

1.3.1.2 加减运算与标量乘法

四元数的加减运算与标量乘法同复数类似，只需将分量各自运算即可，这里不做赘述。与复数相同，四元数的标量乘法同样遵循交换律，即 \(sq = qs\)，其中s为标量。

1.3.1.3 四元数乘法

四元数乘法较为特殊，并不遵循交换律，也就是说在一般情况下\(q_1q_2 ≠ q_2q_1\)。

如果有两个四元数 \(q_1 = a + bi + cj + dk\) 和 \(q_2 = e + fi + gj + hk\) ，由 \(i² = j² = k² = ijk = −1\) 可得其乘积为：
\[ \begin{aligned} &q_{1} q_{2}=a e+a f i+a g j+a h k+\\ &b e i-b f+b g k-b h j+\\ &\begin{array}{l} {c e j-c f k-c g+c h i+} \\ {d e k+d f j-d g i-d h} \end{array}\\ &=(a e-b f-c g-d h)+\\ &(b e+a f-d g+c h) i\\ &(c e+d f+a g-b h) j\\ &(d e-c f+b g+a h) k \end{aligned} \]
写成矩阵形式则有：
\[ q_{1} q_{2}=\left[\begin{array}{cccc} {a} & {-b} & {-c} & {-d} \\ {b} & {a} & {-d} & {c} \\ {c} & {d} & {a} & {-b} \\ {d} & {-c} & {b} & {a} \end{array}\right]\left[\begin{array}{l} {e} \\ {f} \\ {g} \\ {h} \end{array}\right] \]
这个矩阵变换相当于左乘 \(q_1\)，由于四元数不符合交换律，所以右乘\(q_1\)的变换是一个不同的矩阵：
\[ q_{2} q_{1}=\left[\begin{array}{cccc} {a} & {-b} & {-c} & {-d} \\ {b} & {a} & {d} & {-c} \\ {c} & {-d} & {a} & {b} \\ {d} & {c} & {-b} & {a} \end{array}\right]\left[\begin{array}{l} {e} \\ {f} \\ {g} \\ {h} \end{array}\right] \]

1.3.1.4 纯四元数

与复数相似，实部为0的四元数被称之为纯四元数，空间中的三维向量可以用纯四元数的形式表示，这种表示方法在四元数表示旋转的推导过程中有重要应用。

1.3.1.5 单位四元数

定义模长为1的四元数为单位四元数，用于表示旋转的四元数一定为单位四元数。

2 利用四元数表示姿态

该部分省略推导过程，具体可以参考https://krasjet.github.io/quaternion/quaternion.pdf

2.1 利用四元数表示旋转

通过罗德里格旋转，我们可以推导出四元数表示旋转的定理：

任意向量 v 绕着以单位向量定义的旋转轴 u 旋转 θ 度后的 v' 可以使用四元数乘法来获得四元数旋转公式:
\[ v^{\prime}=q v q^{*}=q v q^{-1} \]
其中：
\[ v=[0, \mathbf{v}], \quad q=\left[\cos \left(\frac{1}{2} \theta\right), \sin \left(\frac{1}{2} \theta\right) \mathbf{u}\right]\\ \]

2.2 利用四元数表示姿态矩阵

我们已经得出四元数表示旋转的一般形式，即三个四元数相乘，通过四元数乘法的矩阵表示形式，我们可以将四元数旋转公式表示为矩阵形式：
\[ q v q^{*}=\left[\begin{array}{cccc} {1} & {0} & {0} & {0} \\ {0} & {1-2 q_{2}^{2}-2 q_{3}^{2}} & {2 q_{1} q_{2}-2 q_{0} q_{3}} & {2 q_{0} q_{2}+2 q_{1} q_{3}} \\ {0} & {2 q_{1} q_{2}+2 q_{0} q_{3}} & {1-2 q_{1}^{2}-2 q_{3}^{2}} & {2 q_{2} q_{3}-2 q_{0} q_{1}} \\ {0} & {2 q_{1} q_{3}-2 q_{0} q_{2}} & {2 q_{0} q_{1}+2 q_{2} q_{3}} & {1-2 q_{1}^{2}-2 q_{2}^{2}} \end{array}\right] v \]
矩阵的第一行和第一列不会对v进行任何变换，所以我们可以将其压缩为3维方阵，即可得到矩阵旋转公式：

任意向量 v 沿着以单位向量定义的旋转轴 u 旋转 θ 角度后的 v' 可以使用矩阵乘法来获得：
\[ \mathbf{v}^{\prime}=\left[\begin{array}{ccc} {1-2\left(q_{2}^{2}+q_{3}^{2}\right)} & {2\left(q_{1} q_{2}-q_{0} q_{3}\right)} & {2\left(q_{1} q_{3}+q_{0} q_{2}\right)} \\ {2\left(q_{1} q_{2}+q_{0} q_{3}\right)} & {1-2\left(q_{1}^{2}+q_{3}^{2}\right)} & {2\left(q_{2} q_{3}-q_{0} q_{1}\right)} \\ {2\left(q_{1} q_{3}-q_{0} q_{2}\right)} & {2\left(q_{2} q_{3}+q_{0} q_{1}\right)} & {1-2\left(q_{1}^{2}+q_{2}^{2}\right)} \end{array}\right]\mathbf{v} \]
姿态矩阵C（也称为坐标转换矩阵）即为：
\[ C=\left[\begin{array}{lll} {1-2\left(q_{2}^{2}+q_{3}^{2}\right)} & {2\left(q_{1} q_{2}-q_{0} q_{3}\right)} & {2\left(q_{1} q_{3}+q_{0} q_{2}\right)} \\ {2\left(q_{1} q_{2}+q_{0} q_{3}\right)} & {1-2\left(q_{1}^{2}+q_{3}^{2}\right)} & {2\left(q_{2} q_{3}-q_{0} q_{1}\right)} \\ {2\left(q_{1} q_{3}-q_{0} q_{2}\right)} & {2\left(q_{2} q_{3}+q_{0} q_{1}\right)} & {1-2\left(q_{1}^{2}+q_{2}^{2}\right)} \end{array}\right] \]
其中：
\[ q_{0}=\cos \left(\frac{1}{2} \theta\right), q_{1}=\sin \left(\frac{1}{2} \theta\right) u_{x}, q_{2}=\sin \left(\frac{1}{2} \theta\right) u_{y}, q_{3}=\sin \left(\frac{1}{2} \theta\right) u_{z} \]
对应四元数为：
\[ q=q_{0}^{}+q_{1}^{} i+q_{2}^{} j+q_{3}^{} k \]
也可写成有序数对形式，即2.1旋转公式中的：
\[ \quad q=\left[\cos \left(\frac{1}{2} \theta\right), \sin \left(\frac{1}{2} \theta\right) \mathbf{u}\right]\\ 其中\mathbf{u} = \left[\begin{array}{l} {u_{x}} \\ {u_{y}} \\ {u_{z}} \end{array}\right] \]

2.3 通过四元数反解欧拉角

得到四元数后，可以通过四元数的值反解出机体坐标系的欧拉角，同样的这里省略推导过程直接给出公式：
\[ \left\{\begin{array}{c} {\theta=\arcsin [2(-q_0 q_1+q_2 q_3)]} \\ {\gamma=-\arctan \left(\frac{q_0 q_2+q_1 q_3}{q_0^{2}-q_1^{2}-q_2^{2}+q_3^{2}}\right)} \\ {\psi=-\arctan \left(\frac{q_1 q_2+q_0 q_3}{q_0^{2}-q _1^{2}+q_2^{2}-q_3^{3}}\right)} \end{array}\right. \]

3 基于四元数的姿态解算

3.1 四元数的求解

机体姿态的改变即为四元数的改变，因此对于机体的姿态解算需要实时更新四元数。我们通过构建四元数关于时间的微分方程来研究此问题。考虑到角度与四元数直接相关，因此我们可以利用四元数的三角表示式来建立四元数的微分方程，通过求解该微分方程来求解四元数的值。

存在单位四元数：
\[ Q=\cos \frac{\theta}{2}+\vec{u} \sin \frac{\theta}{2} \]
对时间t进行微分，可得：
\[ \frac{d Q}{d t}=\frac{1}{2}\left[\begin{array}{cccc} {0} & {-\omega_{x}} & {-\omega_{y}} & {-\omega_{z}} \\ {\omega_{x}} & {0} & {\omega_{z}} & {-\omega_{y}} \\ {\omega_{y}} & {-\omega_{z}} & {0} & {\omega_{x}} \\ {\omega_{z}} & {\omega_{y}} & {-\omega_{x}} & {0} \end{array}\right] \cdot\left[\begin{array}{c} {q_{0}} \\ {q_{1}} \\ {q_{2}} \\ {q_{3}} \end{array}\right] \]
求解该微分方程即可得到当前四元数的值。但计算机中的计算是离散的，所以我们需要对该微分方程进行离散化处理，这样才可以有效的通过单片机或其他数字控制器进行求解。

在mahony算法中使用一阶龙格库塔法求解该微分方程，一阶龙格库塔法是一种在工程中求解微分方程常用的方法，应用于四元数微分方程求解可得以下公式：
\[ \left[\begin{array}{l} {q_{0}} \\ {q_{1}} \\ {q_{2}} \\ {q_{3}} \end{array}\right]_{t+\Delta t}=\left[\begin{array}{l} {q_{0}} \\ {q_{1}} \\ {q_{2}} \\ {q_{3}} \end{array}\right]_{t}+\frac{1}{2} \cdot \Delta t \cdot\left[\begin{array}{c} {-\omega_{x} \cdot q_{1}-\omega_{y} \cdot q_{2}-\omega_{z} \cdot q_{3}} \\ {\omega_{x} \cdot q_{0}-\omega_{y} \cdot q_{3}+\omega_{z} \cdot q_{2}} \\ {\omega_{x} \cdot q_{3}+\omega_{y} \cdot q_{0}-\omega_{z} \cdot q_{1}} \\ {-\omega_{x} \cdot q_{2}+\omega_{y} \cdot q_{1}+\omega_{z} \cdot q_{0}} \end{array}\right] \]
最后，通过C语言实现该公式即可迭代出四元数的值

3.2 传感器数据融合

3.2.1 基本原理

通过一阶龙格库塔法得到的微分方程中存在角速度变量，保证角速度数据的准确性是极为重要的。

首先，对于六轴数据，计算角度有两种方法，一种是通过对角速度积分得到角度，另一种则是通过对加速度进行正交分解得到角度。但这两种方式均存在不足，通过角速度积分得到角度时，角速度的误差会在积分过程中被不断放大从而影响数据准确性。而加速度计是一种特别敏感的传感器，电机旋转产生的震动会给加速度计的数据中带来高频噪声。

不难看出，第一种方法测得的数据中存在低频噪声，而第二种方法测得的数据中存在高频噪声，因此可通过向量外积补偿也就是我们常说的互补滤波来进行数据融合。

设有大地坐标下的重力加速度 g，把 g 通过姿态矩阵（坐标转换矩阵）转换到机体坐标系，得到其在机体上的理论重力加速度向量 \(\hat{\boldsymbol{v}}\) ，则两者的转换关系可通过前文给出的姿态矩阵得出：
\[ \hat{\boldsymbol{v}}=C \cdot \mathbf{g}=\left[\begin{array}{lll} {1-2\left(q_{2}^{2}+q_{3}^{2}\right)} & {2\left(q_{1} q_{2}-q_{0} q_{3}\right)} & {2\left(q_{1} q_{3}+q_{0} q_{2}\right)} \\ {2\left(q_{1} q_{2}+q_{0} q_{3}\right)} & {1-2\left(q_{1}^{2}+q_{3}^{2}\right)} & {2\left(q_{2} q_{3}-q_{0} q_{1}\right)} \\ {2\left(q_{1} q_{3}-q_{0} q_{2}\right)} & {2\left(q_{2} q_{3}+q_{0} q_{1}\right)} & {1-2\left(q_{1}^{2}+q_{2}^{2}\right)} \end{array}\right] \cdot\left[\begin{array}{l} {0} \\ {0} \\ {1} \end{array}\right]=\left[\begin{array}{c} {2\left(q_{1} q_{3}+q_{0} q_{2}\right)} \\ {2\left(q_{2} q_{3}-q_{0} q_{1}\right)} \\ {1-2\left(q_{1}^{2}+q_{2}^{2}\right)} \end{array}\right]=\left[\begin{array}{c} {v_{ x}} \\ {v_{ y}} \\ {v_{ z}} \end{array}\right] \]
不难看出，将重力加速度向量转换至机体坐标系后，恰好是姿态矩阵的最后一列，因此，四元数或者说姿态矩阵是可以和理论重力加速度相互推导的，即姿态矩阵的第三列的列向量就是算法中理论重力加速度向量。

除了由四元数推导出的理论重力加速度向量 \(\hat{\boldsymbol{v}}\) ，我们还可以通过加速度计测量出实际重力加速度向量 \(\overline{\boldsymbol{v}}\) 。

很显然，这里的理论重力加速度向量 \(\hat{\boldsymbol{v}}\) 和实际重力加速度向量 \(\overline{\boldsymbol{v}}\) 之间必然存在偏差，这个偏差很大程度上是由陀螺仪数据产生的角速度误差引起的，所以我们通过消除理论向量和实际向量间的偏差，就可以补偿陀螺仪数据的误差，进而解算出较为准确的姿态。

3.2.2 误差补偿

通过向量外积表示误差，理论重力加速度向量和实际重力加速度向量均是向量，含有向量间夹角关系的运算有两种：内积（点乘）和外积（叉乘），在Mahony算法中通过计算外积来得到向量方向差值 θ：
\[ |\mathbf{ρ}|=|\overline{\boldsymbol{v}}| \cdot|\hat{\boldsymbol{v}}| \cdot \sin \theta \]
在进行叉乘运算前，应先将理论向量 \(\hat{\boldsymbol{v}}\) 和实际向量 \(\overline{\boldsymbol{v}}\) 做单位化处理，因此上式可化为：
\[ |\mathbf{ρ}|=\sin \theta \]
考虑到实际情况中理论向量 \(\hat{\boldsymbol{v}}\) 和实际向量 \(\overline{\boldsymbol{v}}\) 偏差角不会超过45°，而当 θ 在±45°内时，sinθ 与 θ的值非常接近，因此上式可进一步简化为：
\[ |\mathbf{ρ}|=\theta \]
构建PI控制器来控制补偿值的大小，公式如下：
\[ GyroError=K_{P} \cdot \text { error }+K_{I} \cdot \int \text {error} \]
其中，比例项用于控制传感器的“可信度”，积分项用于消除静态误差。Kp越大，意味着通过加速度计得到的误差所对应的补偿越显著，也就是越信任加速度计，反之Kp越小时，加速度计对陀螺仪的补偿作用越弱，也就是月信任陀螺仪。至于积分项的作用和参数意义笔者还没完全弄懂就先不瞎扯了。

得到补偿值之后，我们就可以将补偿值补偿到角速度上，即可得到更准确的角速度数据，而后将补偿后的角速度数据带入通过一阶龙格库塔法得到的四元数微分方程中即可求解（更新）当前四元数，在更新四元数后，我们就得到了新的理论重力加速度向量，从而可以重复上述过程来持续进行误差补偿。

该误差补偿过程框图如下：

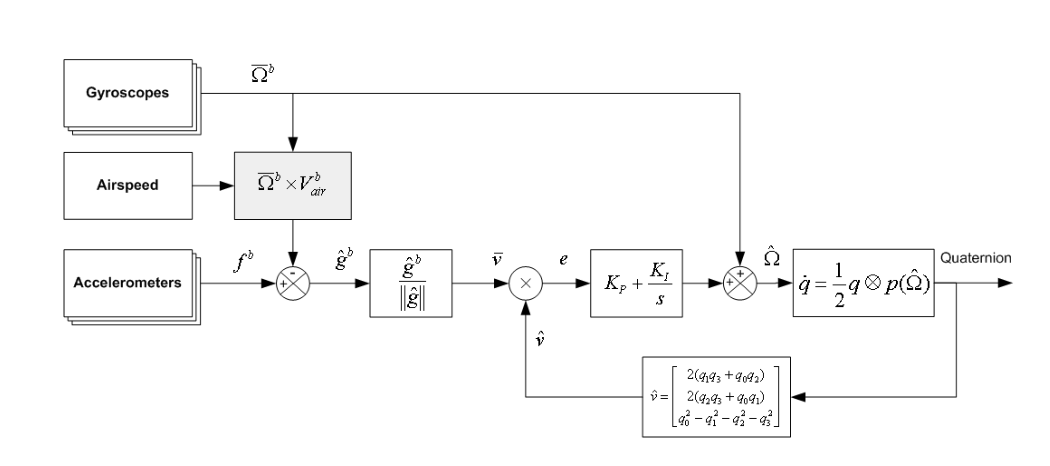
3.3 回到欧拉角

我们通过传感器数据融合得到了较准确的四元数，但四元数描述姿态本身不够直观，为了方便对系统的姿态控制，我们在最后还需要通过四元数反解出欧拉角，通过欧拉角进行姿态控制中的各种闭环控制。这里直接套用上文给出的公式即可：
\[ \left\{\begin{array}{c} {\theta=\arcsin [2(-q_0 q_1+q_2 q_3)]} \\ {\gamma=-\arctan \left(\frac{q_0 q_2+q_1 q_3}{q_0^{2}-q_1^{2}-q_2^{2}+q_3^{2}}\right)} \\ {\psi=-\arctan \left(\frac{q_1 q_2+q_0 q_3}{q_0^{2}-q _1^{2}+q_2^{2}-q_3^{3}}\right)} \end{array}\right. \]

3.4 代码分析

void MahonyAHRSupdateIMU(float q[4], float gx, float gy, float gz, float ax, float ay, float az) {
    float recipNorm;
    float halfvx, halfvy, halfvz;
    float halfex, halfey, halfez;
    float qa, qb, qc;

    // Compute feedback only if accelerometer measurement valid (avoids NaN in accelerometer normalisation)
    // 只在加速度计数据有效时才进行运算
    if(!((ax == 0.0f) && (ay == 0.0f) && (az == 0.0f))) {

        // Normalise accelerometer measurement
        // 将加速度计得到的实际重力加速度向量v单位化
        recipNorm = invSqrt(ax * ax + ay * ay + az * az); //该函数返回平方根的倒数
        ax *= recipNorm;
        ay *= recipNorm;
        az *= recipNorm;        

        // Estimated direction of gravity
        // 通过四元数得到理论重力加速度向量g
        halfvx = q[1] * q[3] - q[0] * q[2];
        halfvy = q[0] * q[1] + q[2] * q[3];
        halfvz = q[0] * q[0] - 0.5f + q[3] * q[3];
    
        // Error is sum of cross product between estimated and measured direction of gravity
        // 对实际重力加速度向量v与理论重力加速度向量g做外积
        halfex = (ay * halfvz - az * halfvy);
        halfey = (az * halfvx - ax * halfvz);
        halfez = (ax * halfvy - ay * halfvx);

        // Compute and apply integral feedback if enabled
        // 在误差补偿PI控制器中积分项使能情况下计算并应用积分项
        if(twoKi > 0.0f) {
            // integral error scaled by Ki
            // 积分过程
            integralFBx += twoKi * halfex * (1.0f / sampleFreq);    
            integralFBy += twoKi * halfey * (1.0f / sampleFreq);
            integralFBz += twoKi * halfez * (1.0f / sampleFreq);
            
            // apply integral feedback
            // 应用误差补偿中的积分项
            gx += integralFBx;  
            gy += integralFBy;
            gz += integralFBz;
        }
        else {
            // prevent integral windup
            // 避免为负值的Ki时积分异常饱和
            integralFBx = 0.0f; 
            integralFBy = 0.0f;
            integralFBz = 0.0f;
        }

        // Apply proportional feedback
        // 应用误差补偿中的比例项
        gx += twoKp * halfex;
        gy += twoKp * halfey;
        gz += twoKp * halfez;
    }
    
    // Integrate rate of change of quaternion
    //一阶龙格库塔法迭代四元数
    gx *= (0.5f * (1.0f / sampleFreq));     // pre-multiply common factors
    gy *= (0.5f * (1.0f / sampleFreq));
    gz *= (0.5f * (1.0f / sampleFreq));
    qa = q[0];
    qb = q[1];
    qc = q[2];
    q[0] += (-qb * gx - qc * gy - q[3] * gz); //微分方程本身
    q[1] += (qa * gx + qc * gz - q[3] * gy);
    q[2] += (qa * gy - qb * gz + q[3] * gx);
    q[3] += (qa * gz + qb * gy - qc * gx); 
    
    // Normalise quaternion
    // 单位化四元数 保证四元数在迭代过程中保持单位性质
    recipNorm = invSqrt(q[0] * q[0] + q[1] * q[1] + q[2] * q[2] + q[3] * q[3]);
    q[0] *= recipNorm;
    q[1] *= recipNorm;
    q[2] *= recipNorm;
    q[3] *= recipNorm;
    
    //Mahony官方程序到此结束，使用时只需在函数外进行四元数反解欧拉角即可完成全部姿态解算过程
}