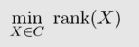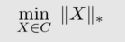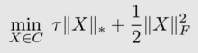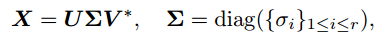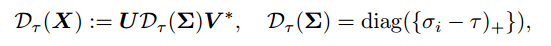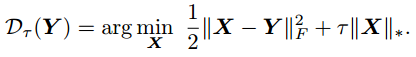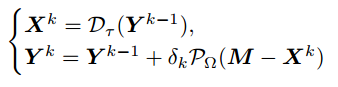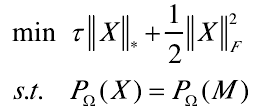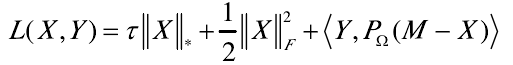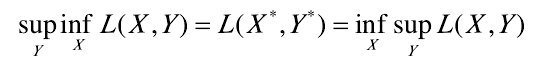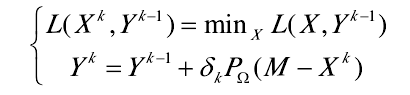Singular Value Thresholding (SVT) 奇异值阈值

[本文链接：http://blog.csdn.net/shanglianlm/article/details/46009387，转载请注明出处]

为了求解问题

因为它是非凸的，我们求解一个它的近似算法

对于一个大的ττ值，它可以用下列等式接近

其中第一项为核范式（奇异值的和），第二项为Frobenius范式。

1. Singular Value Thresholding (SVT) 奇异值阈值

   * 奇异值收缩(singular value shrinkage)*

   首先我们考虑一个秩为rr的矩阵X∈Rn1xn2X∈Rn1xn2的奇异值分解如下： 
    
   其中 UU 和 VV 分别为 n1×rn1×r 和 n2×rn2×r 的正交矩阵，奇异值为ρiρi非负的。

   对于每个τ≥0τ≥0，我们有软阈值操作DτDτ: 
    
   其中t+t+表示的tt非负部分，即 t+=max(0,t)t+=max(0,t)。换句话说，这个软阈值操作仅仅应用于矩阵 XX 的奇异值上，使它们趋于零。这也是为什么我们将其成为奇异值收缩(singular value shrinkage)的原因。

   * Singular Value Thresholding (SVT) 奇异值阈值*

   又因为奇异值收缩(singular value shrinkage)是核范式的近似操作(具体证明见[3])，因此上式可以转化为： 
   

   它的迭代方式为： 
   

   这个算法受到压缩感知中迭代算法的启发，在迭代过程中对矩阵进行SVD，然后将较小的奇异值设置为0，生成新的矩阵进行迭代。该算法运算速度快，对于高位低秩矩阵的恢复非常有效。

2. 用拉格朗日乘子法解释

   原问题为：

   

   其拉格朗日函数为：

   

   强对偶成立，且拉格朗日函数的鞍点是原函数与对偶问题的最优解，即

   

   其迭代解为：

   

参考或延伸材料： 
[1] 斯坦福SVT软件 
[2] Generalized Singular Value Thresholding 
[3] A singular value thresholding algorithm for matrix completion 
[4] Exact Matrix Completion via Convex Optimization

版权声明：本文为博主原创文章，欢迎转载，转载请注明出处。 https://blog.csdn.net/shanglianlm/article/details/46009387