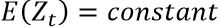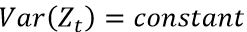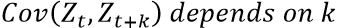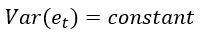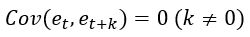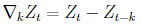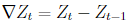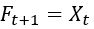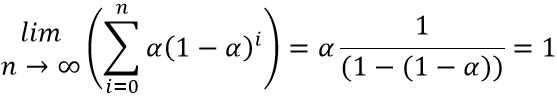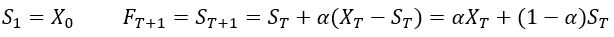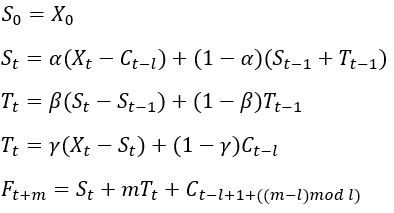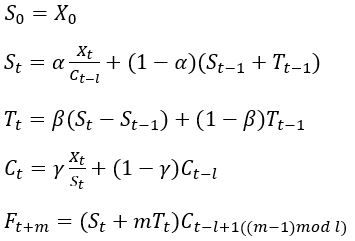时间序列有三种基本模式:
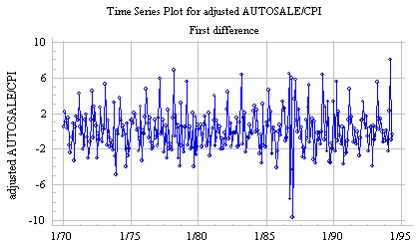
平稳性 / 随机性(Stationarity):当数据没有明显的模式特征的话,我们认为它是平稳的,Y值在一个范围内随着时间上下浮动。
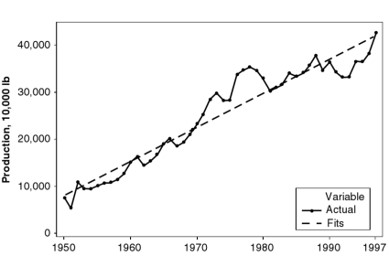
趋势性(Trend):当Y值在一段时间内随着时间有明显的向上或者向下的趋势的时候,我们认为有趋势性。
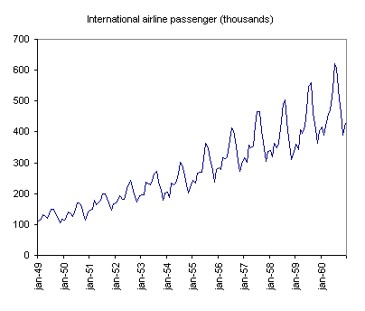
季节性(Seasonarity):当Y值在某个固定的时间内,有明显的波动,我们认为存在季节性。举个例子,降雨量大的时间通常在春夏两季,而在秋冬两季则明显减少。下图所示的图同时具有趋势性和季节性。
在时间序列预测的过程中,我们首先要判断数据是否具有上述的特征,除去上述趋势性和季节性的特征,使其达到平稳状态,这一点对于准确地预测数据有至关重要的作用。
平稳性(Stationarity)
一组平稳的数据意味着它在一段时间内围绕着在一个范围内上下浮动,要达到平稳,需要达到三个条件:
1.期望值(均值)为常数
2.方差为常数
3.只要K固定,任意两个相隔K个时间段的数据组的协方差相同的(也就是说协方差只依赖于K这个时间跨度,不依赖于时间点t本身)
平稳的序列中随机变量会大量地减少,因此有助于我们进行预测。平稳化序列是时间序列中重要的一步,这一步应该在对数据建模之前就应该完成。
判断是否序列是否平稳的方法:
1. Augmented Dickey-Fuller(ADF)-test
2. Kwiatkowski-Phillips-Schmidt-Shin(KPSS)-test
趋势性(Trend)
在时间序列中,趋势分为确定性趋势和随机性趋势两种,确定性趋势从直观上讲是指序列的趋势不是变幻莫测,而是可以用一条趋势线来拟合的,当去除掉趋势的部分后,该序列就变成平稳的序列,这也是上述“趋势平稳”的意思;现实中还会有一种时间序列是随机性趋势的,趋势无法通过单一的趋势性描绘,在不同时间,趋势是随机变化的,这种情况下单位根过程则是一种有效的刻画工具(在这里不展开,以后有待进一步研究)。
判断是否有趋势:
Mann-Kendall(MK)-test
白噪声(White Noise)
白噪声是指一组时间序列中,任意选取两个时间,数据毫不相关的序列。它意味着该时间序列是纯随机的,可以理解为其中没有任何有提取价值的信息。
白噪声的三个条件:
1.期望值(均值)为0
2.方差为常数
3.当K不等于0时,任意两个时间点的数据的协方差为0
判断是否白噪声的方法:
Ljung-Box test是一种判断序列的自相关函数是否为0的统计方法,是一种白噪声检验法。
Q统计值服从卡方分布,自由度选取上式的h作为参数。
Ljung-Box test通常用在ARIMA模型的残差上,并不会用在原始数据上。
差分(Differencing)
差分是指序列中相隔k阶的数据相减的一个操作,定义如下:
其中Z为时间序列,t为序列的项数,k为差分的阶数,比如一阶差分如下:
差分是使时间序列得以平稳的一个很重要的过程,但是差分的阶数选择不对,或者差分的次数过多,反而会丢失太多时间序列的信息。
几个使原始序列平稳的小技巧:
1.如果序列波动很大,也就是方差比较大,可以对序列作对数转换以减缓其波动幅度
2.如果序列存在明显趋势,且呈现近似一条直线的趋势,可以对序列作一阶差分,从而消除趋势性
3.如果序列存在明显的S期季节性,则可对序列作S阶差分,从而消除季节性
原始时间序列经过了预处理和各种检验之后,可以对处理过的时间序列进行建模拟合,有多种模型对序列进行拟合。
Naive模型
这个模型基本没有什么技术含量,单纯地把上期的真实值作为下期的预测值,主要是作为参照模型而存在的,如果拟合出来的模型比这个模型的误差还大的话,那就是瞎猜的都比拟合的模型要好(囧)
其中F为预测值,X为真实值
指数平滑模型(Exponential Smoothing)
指数平滑模型是一种常见的时间序列建模方法,数据按时间顺序从新到旧排列,权重也会由大到小地分配,也就是说新的数据会被赋予相对较高的权重,旧的数据则会是相对较低的权重,并且权重值是指数型下降的。
因为α是指数式下降的,因此把所有的α加起来等于1
α的选择经验之谈:
1. 时间序列平稳的时候,也就是过去的数据与当前数据对比模式基本一样,我们可以认为过去的数据也是重要的,有利于对未来的预测,因此α取值较小,一般在0.05~0.2之间
2. 时间序列有波动但幅度不大的时候,可以认为过去数据有异常情况不适合对未来预测,但是因为幅度不大因此也有一定参考价值,α可稍微取大一点的值,一般在0.1~0.4之间
3. 时间序列有较大波动的时候,可以认为过去数据变化太大出现短暂不可预测的异常(有可能遇到了金融海啸等),这时一般α的取值可以较大,在0.6~0.8之间
4. 时间序列有明显的上升或者下降趋势的时候,可以认为过去的数据有一定的参考价值,但是并不是十分重要的,因此此时α的取值范围比较大,需要根据实际情况确定,一般取值在0.6~1之间
(参考来源:百度百科)
单指数平滑模型(Single Exponential Smoothing)
模型只有一个参数项α,分别用上一期赋予权重的真实值和预测值来计算下一期的预测值,适合平稳没有趋势性和季节性的数据
其中X为真实值,S为平滑项,α为平滑指数,F为预测值
双指数平滑模型(Double Exponential Smoothing)
跟单指数平滑模型相比,其因为含有单调趋势,因此由平滑项和趋势项两个系数项组成
模型有两大流派:Brown单参数线性指数平滑模型和Holt's(Holt-Winters)双参数线性指数平滑模型,适合有单调趋势但没有季节性的数据
注:它们的名字都有很多,只要记住它们基本都是线性的指数平滑模型,Brown是单参数流的,Holt's(Holt-Winters)则是双参数流的
Brown指数平滑模型(Brown Double Exponential Smoothing)
其中Brown流派又分为自适应的Brown指数平滑模型和非自适应的Brown指数平滑模型
自适应Brown在每一期的预测都会更新参数,本文将不展开,以后有待学习!
非自适应Brown指数平滑模型只有一个参数α(0<α<1),无论是平滑项还是趋势项都由α控制,具体公式如下:
其中X为真实值,S为平滑项,T为趋势项,F为预测值,m为预测的期数
Holt's指数平滑模型(Holt's Exponential Smoothing)
Holt's指数平滑模型有两个参数α和β,α负责平滑项系数,β则负责趋势项,具体公式如下:
其中X为真实值,S为平滑项,T为趋势项,F为预测值,m为预测的期数
Brown流派和Holt's流派的对比
两者相比,就灵活性而言无疑是Holt's更胜一筹,毕竟它有两个参数,而Brown只有一个,一般来讲Holt's模型的预测精度要比Brown高。Brown的优势则主要在于只需要一个参数,因此当参数需要频繁修改的时候,Brown更方便也更好找最优参数。
三指数平滑模型(Triple Exponential Smoothing)
与前面的模型相比,三指数平滑模型把季节性也考虑进模型,因此模型有三个参数α,β和γ,适合带有季节性规律的数据。
三指数平滑模型只有Holt-Winters一个流派,不过该流派也分加法模型和乘法模型两种模型
加法模型(Holt-Winters Additive Tiple Exponential Smoothing)如下:
其中X为真实值,S为平滑项,T为趋势项,C为季节项(周期项),l为周期期数,F为预测值,m为预测的期数
乘法模型(Holt-Winters Multiplicative Triple Exponential Smoothing)如下:
其中X为真实值,S为平滑项,T为趋势项,C为季节项(周期项),l为周期期数,F为预测值,m为预测的期数
加法模型和乘法的区别
加法模型中单个因子的效应被区分开来,它人为地忽略了相互之间的作用;乘法模型则考虑了相互的作用,随着数据的值增大,季节性的量也随之增长,大多数时间序列都展现这种模式。当数据中季节性的量取决于数据值的时候 ,应该选择乘法模型;当季节性的量不取决于数据值的时候,应该选择加法模型,当然,如果不清楚的时候两种都应该尝试。
ARIMA(Auto Regressive Integrated Moving Average)模型
对于时间序列的建模预测,除了指数平滑(Exponential Smoothing)这样根据参数按指数式递减的方式去平滑化数据继而拟合之外,还有很常见的用ARIMA模型拟合的方法。ARIMA由三部分组成,自回归过程(AR),差分部分(Integrated)和移动平均过程。一般来讲,如果时间序列的自相关函数(Autocorrelation Funtion)拖尾(随着阶数逐渐衰减)而偏相关函数(Partial Autocorrelation Function)在某阶截尾(某阶后自相关函数都等于0),这样的序列适合用自回归过程(Auto Regressive)拟合;如果自相关函数某阶截尾,偏相关函数拖尾,则适合用移动平均(Moving Average);如果两个函数都拖尾,我们可以用ARIMA模型来拟合。
ARIMA的公式如下:
其中p为自回归模型的阶数,d为差分阶数,q为移动平均模型的阶数,Z是时间序列数据,B为后移算子(Backshift Operator),φ和θ分别为自相关过程的系数和移动平均过程的系数,a为白噪声。
注:后移算子的存在是其乘上相对应的系数就变成了过程的某阶,举个例子,自相关过程中,k=3,乘上相对应的系数φ就变成了自相关过程的第三阶。
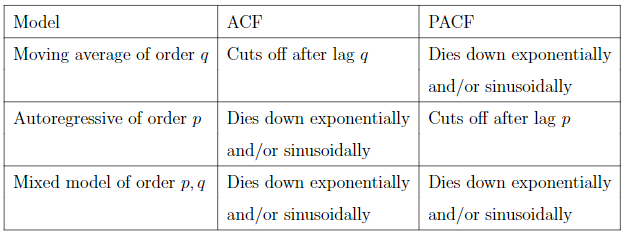
AR(p),MA(q)和ARMA(p,q)各自的性质如下表:
判断ARIMA(p,q)模型系数的方法:
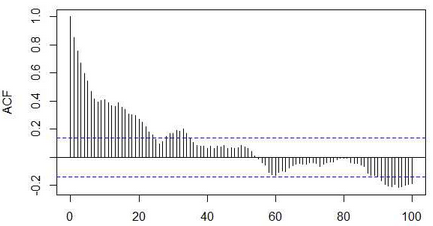
我们可以通过观察时间序列的自相关函数图(Autocorrelation Funcion Plot)及偏相关函数图(Partial Autocorrelation Funtion Plot)来判断ARIMA的p和q系数。如下图的例子,我们看出ACF图中随着阶数的增加,ACF系数是呈拖尾状态不断衰减的;而PACF图中系数在1阶的时候就早早地截尾了。因此根据ARMA模型的系数特点,我们初步可以判断出这个时间序列适合用ARMA(1,0)来拟合。