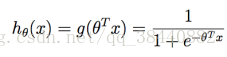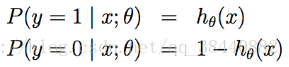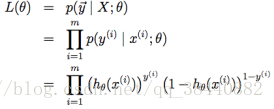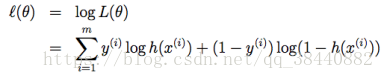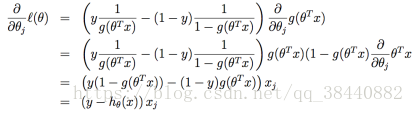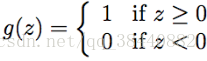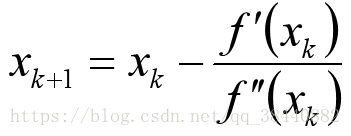分类和逻辑回归
在之前说过了线性回归的一些问题,线性回归常常用在一些预测值为连续的情况下,但生活中有的结果是以离散的形态分布的,比如下雨还是不下雨,浏览到新闻会点击还是不会点击,看到商品买还是不买,这些都是有特定的结果类别的,我们称这一类问题为分类问题
对于二元分类的问题,从线性的角度来看,最终的预测值依然是连续的,但我们可以对于预测的值设定一个阈值,当预测值超过这个值则另结果为1,否则为0,因为y ∈ {0, 1},所以我们的模型函数最终的值也在0和1之间,我们用sigmoid(logistic) function来表示这个函数
其中
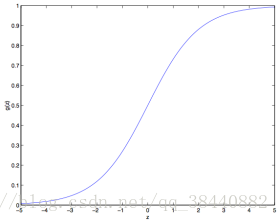
函数图像如下
时
时
对分类模型做一些统计学假设
更简洁的可以写为:
可以分别代入0和1验证上面的式子,上面这个式子其实是一个指数族的分布的形式,在后面的内容会进行讲解
假设m个训练样本都是独立的,所以可以按照下面的形式写参数的似然函数
和之前的似然函数处理方式一样,这里也取对数方便计算
同样,我们还是需要求最大似然,因为这里是求最大值,所以采用梯度上升算法求最大似然。定义梯度上升的更新规则如下。
对似然函数求导数
利用了sigmoid函数中的性质 得到了最终的上升规则
感知器学习算法
对逻辑回归方法修改一下,“强迫”它输出的值要么是 0 要么是 1。要实现这个目的,很自然就应该把函数 g 的定义修改一下,改成一个阈值函数(threshold function)
如果我们还像之前一样令 hθ(x) = g(θT x),但用刚刚上面的阈值函数作为 g 的定义,然后如果我们用了下面的更新规则:
这样我们就得到了感知器学习算法。
牛顿方法
上面讲的是梯度上升求的最大似然,实际上在某些情况下,存在一种比梯度迭代更快收敛的一种迭代方法,即牛顿方法。
下面是对牛顿法的图解:
在最左边的图里面,可以看到函数 f 就是沿着 y=0 的一条直线。这时候是想要找一个 θ 来让 f(θ)=0。这时候发现这个 θ 值大概在 1.3 左右。加入咱们猜测的初始值设定为 θ=4.5。牛顿法就是在 θ=4.5 这个位置画一条切线(中间的图)。这样就给出了下一个 θ 猜测值的位置,也就是这个切线的零点,大概是2.8。最右面的图中的是再运行一次这个迭代产生的结果,这时候 θ 大概是1.8。就这样几次迭代之后,很快就能接近 θ=1.3。
证明如下:
所以通过令f(θ) = l′(θ)=0,咱们就可以同样用牛顿法来找到 l 的最大值,然后得到下面的更新规则:
同样,这个规则也可以从泰勒展式中推出:
若f(x)二阶导连续,将f(x)在xk处Taylor展开
最后,在咱们的逻辑回归背景中,θ 是一个有值的向量,所以我们要对牛顿法进行扩展来适应这个情况。牛顿法进行扩展到多维情况,也叫牛顿-拉普森法(Newton-Raphson method),如下所示:
牛顿方法通常都能比梯度下降法速度更快,因为在牛顿方法的更新规则中,误差变为了之前的平方,收敛更快(即具有二次收敛的特性)