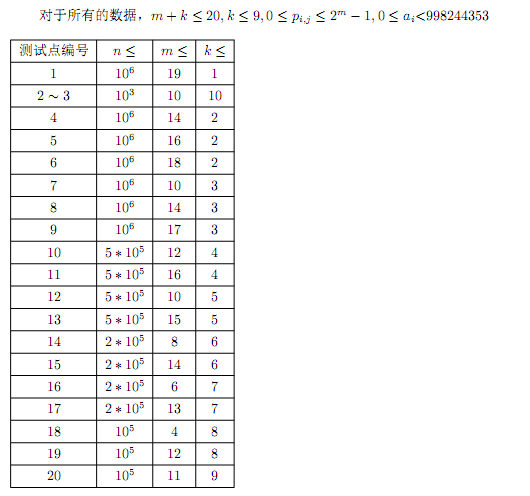
题目描述

题解
吼题
推荐博客:https://www.cnblogs.com/jz-597/p/12300760.html
最暴力的做法是把n个2^m的FWT乘起来,这样显然不行
先把pi,1~k异或上pi,1,把pi,1变为0,最后再把pi,1异或回去
考虑FWT(xor)的本质,tr(A)=(tr(A1)+tr(A2),tr(A1)-tr(A2)),倒着做可以发现只有变换的u和u+2^k(u&2^k=0)只有u+2^k--->u+2^k这一操作时才需要变号
要求FWT(A)i,就等于把j=0~N-1(N表示FWT的大小,注意大小写)通过不断变号最后加到位置i,变换的实质是把j从后往前一位位变成i
根据上面的结论,只有i和j在当前位都为1时才会变号
记|x|表示x中1的位数,所以\(FWT(A)_i=∑_{j=0}^{N-1}{(-1)^{|i\&j|}A_j}\)
n个FWT的每一位只有2^(k-1)种取值(a1必然为正,x&0=0),因此第\(I\)(注意大小写)位的乘积可以表示成\(\prod\)每种取值^出现次数
考虑求出每个\(I\)的2^(k-1)种乘积的出现次数,然后求出FWT的积,最后IFWT还原出答案
然而直接求出现次数不好求,考虑用FWT(第二种,不同于上面的)来搞
因为FWT实质上是每一位乘上系数再求和,所以可以把每一位分开求
暴力FWT时在pi,2位置上加上a2,则FWT后位置\(I\)的a2系数为\((-1)^{|I\&p_{i,2}|}\)
在pi,2上+1,FWT后可以得到piFWT后第\(I\)位的a2系数
若把i=1~n的pi,2都+1,FWT后得到的则是p1~nFWT后第\(I\)位的a2系数之和,即第\(I\)位所乘的数中a2为正的个数-a2为负的个数
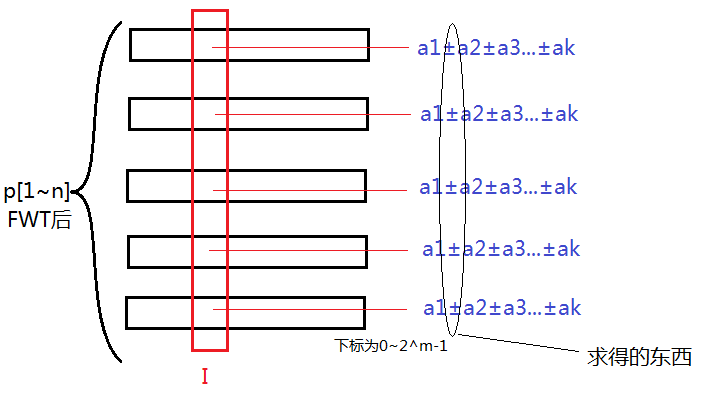
如图,求得的东西就是第\(I\)位中a2的系数之和,等于正数-负数个数
假设k=3,设x0=a1+a2+a3,x1=a1-a2+a3,x2=a1+a2-a3,x3=a1-a2-a3
那么求得的a2正-a2负=x0+x2-x1-x3
同理,在pi,3处+1可得x0+x1-x2-x3
加上最初的x0+x1+x2+x3=n,一共有3条方程4个未知数,无法解
考虑在pi,2⊕pi,3的位置+1,看看得到什么
首先有一条式子:a&(b⊕c)=(a⊕b)&(a⊕c)
证明:若a的某一位为0,则左右两边都为0,否则都为b⊕c
那么FWT后第\(I\)位为\((-1)^{|I\&(p_{i,2} \bigoplus p_{i,3})|}\),由上可知等于\((-1)^{|I\&(p_{i,2})|}*(-1)^{|I\&(p_{i,3})|}\)
把正看成0,负看成1,乘看成异或,则符号满足位运算的性质,这个东西就是a2与a3的符号的异或,求得的是(异或为正-异或为负)
所以同上可得x0-x1-x2+x3
推广一下,一共有2^(k-1)个未知数,枚举子集异或共有2^(k-1)-1条方程,加上∑xi=n共2^(k-1)条,可以高斯消元
但是消元太慢了,观察一下n=4时FWT的结果
{a,b,c,d}-->{a+b+c+d,a-b+c-d,a+b-c-d,a-b-c+d}
和x的关系完全一致,所以把求得的方程按照顺序(-1看成1,2~k对应二进制从低到高)排好后IFWT(第三种,不同于之前的两种)即可
证明见https://blog.csdn.net/zxyoi_dreamer/article/details/104188934
∑xi=n不必特判,因为当第0位为n时FWT后每一位都为n
注意三种FWT/IFWT的大小与含义差别
code
#include <algorithm>
#include <iostream>
#include <cstring>
#include <cstdlib>
#include <cstdio>
#define fo(a,b,c) for (a=b; a<=c; a++)
#define fd(a,b,c) for (a=b; a>=c; a--)
#define mod 998244353
#define two 499122177
#define file
using namespace std;
int P[10]={0,1,2,4,8,16,32,64,128,256};
int p[1000001][10];
long long a[21];
long long A[1048576];
long long b[1048576];
long long c[1048576];
long long p2[1048576];
long long sum[512];
int n,m,m2,K,k2,i,j,k,l,S;
long long qpower(long long a,int b)
{
long long ans=1;
while (b)
{
if (b&1)
ans=ans*a%mod;
a=a*a%mod;
b>>=1;
}
return ans;
}
void fwt(int st,long long *a,int N,int len,int type)
{
int i,j,k,l,s1=2,s2=1,S=N;
long long u,v;
fo(i,1,len)
{
S/=2;
fo(j,0,S-1)
{
fo(k,0,s2-1)
{
u=a[st+j*s1+k];
v=a[st+j*s1+k+s2];
if (type==1)
a[st+j*s1+k]=(u+v)%mod,a[st+j*s1+k+s2]=(u-v)%mod;
else
a[st+j*s1+k]=(u+v)*two%mod,a[st+j*s1+k+s2]=(u-v)*two%mod;
}
}
s1*=2,s2*=2;
}
}
void dg(int t,int s1,long long s2)
{
int i;
if (t>K)
{
memset(c,0,8*m2);
sum[s1]=s2;
fo(i,1,n)
++c[p2[i]];
fwt(0,c,m2,m,1);
fo(i,0,m2-1)
b[i*k2+s1]=c[i];
return;
}
dg(t+1,s1,(s2+a[t])%mod);
fo(i,1,n) p2[i]^=p[i][t];
dg(t+1,s1|P[t-1],(s2-a[t])%mod);
fo(i,1,n) p2[i]^=p[i][t];
}
int main()
{
freopen("yuyuko.in","r",stdin);
#ifdef file
freopen("yuyuko.out","w",stdout);
#endif
scanf("%d%d%d",&n,&m,&K);m2=qpower(2,m),k2=qpower(2,K-1); //2^(k-1)
fo(i,1,K)
scanf("%lld",&a[i]);
fo(i,1,n)
{
fo(j,1,K)
scanf("%d",&p[i][j]);
S^=p[i][1];
fd(j,K,1)
p[i][j]^=p[i][1];
}
// ---
dg(2,0,a[1]); //1
fo(i,0,m2-1) //2
{
fwt(i*k2,b,k2,K-1,-1);
A[i]=1;
fo(j,0,k2-1)
A[i]=A[i]*qpower(sum[j],b[i*k2+j])%mod;
}
// ---
fwt(0,A,m2,m,-1);
fo(i,0,m2-1)
printf("%lld ",(A[i^S]+mod)%mod);
printf("\n");
fclose(stdin);
fclose(stdout);
return 0;
}