Random Variable
\(\underline{cdf:}\)cumulative distribution function \(F(x)=P(X \leq x)\)
\(\underline{pmf:}\)probability mass function(for discrete probability distribution )
(1)\(p(x) \geq0,x \in X\)
(2)\(\sum\limits_{x \in X}P(x)=1\)
\(\underline{pdf:}\)probability density function(for continuous probability distribution )
(1)\(f(x) \geq 0\)for all x,
(2)\(\int_{-\infty}^{\infty}f(x)dx=1\)
discrete distribution:
Negative Binomial Distribution
\(\left(\begin{array}{c}{k+r-1} \\ {k}\end{array}\right)=\frac{(k+r-1) !}{k !(r-1) !}=\frac{(k+r-1)(k+r-2) \ldots(r)}{k !}=(-1)^{k} \frac{(-k-r+1)(-k-r+2) \ldots(-r)}{k !}=(-1)^{k}\left(\begin{array}{c}{-r} \\ {k}\end{array}\right)\)
continuous distribution:
Normal distibution:\(\int_\limits{\mathbb{R}} \exp \left(-\frac{x^{2}}{2}\right) \mathrm{d} x=1\)
\(\int_{0}^{\infty}\exp \left(-\frac{x^{2}}{2}\right) \mathrm{d} x=\frac{1}{2}\)
\(X \looparrowright N(\mu,\sigma^2)\)
pdf:\(p(x)=\frac{1}{\sqrt{2\pi}\sigma}e^{\frac{-(x-\mu)^2}{2\sigma^2}}\)
cdf:\(F(x)=\frac{1}{\sqrt{2\pi}\sigma}\int_{-\infty}^xe^{\frac{-(t-\mu)^2}{2\sigma^2}}dt\)
统计量
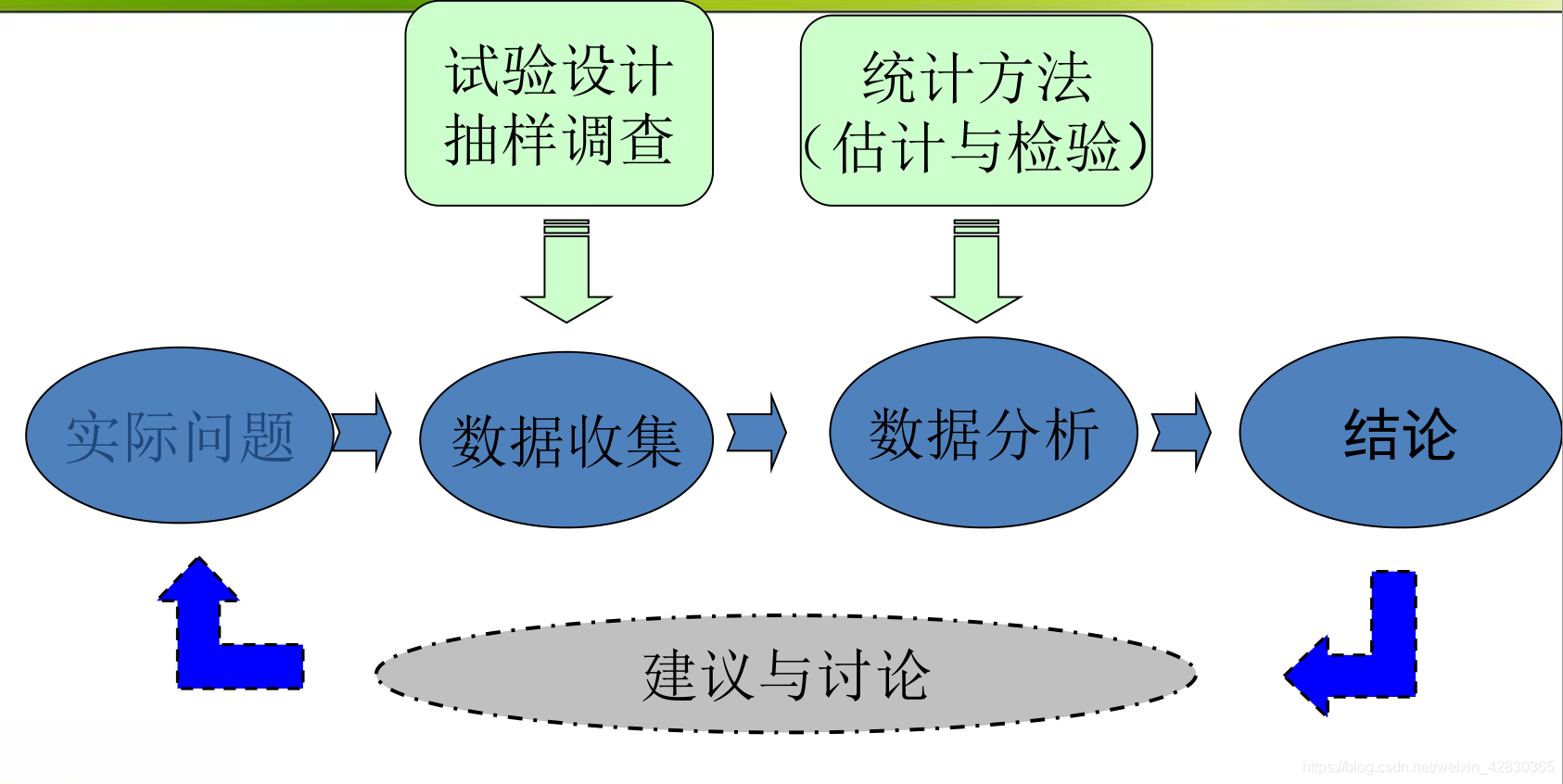

现代统计学时期:
20世纪80年代开始,随着现代生物医学的发展,计算机技术的进步,人类对健康的管理和疾病的治疗已进入基因领域,对基因数据分析产生大量需求。多维海量的基因数据具有全新的数据特征,变量维度远远大于样本数,传统的统计方法失效了,因此一系列面向多维数据的统计分析方法相继产生,比如著名的Lasso方法。
20世纪90年代以来,随着Internet的发展,数据库中积累了海量的数据。如何从海量的数据中挖掘有用的信息就变得越来越重要了,数据挖掘也就应运而生了。与数据挖掘比较接近的名词是机器学习,。因为机器学习算法中涉及了很多的统计学理论,与统计学的关系密切,也被称为统计学习。
经验分布函数:
将所得数据\(x_1,x_2,\dots,x_n\)重新排列为顺序统计量\(x_{1}^{*} \leq x_{2}^{*} \leq \cdots \leq x_{n}^{*}\)
\(F_{n}^{*}(x)=\left\{\begin{array}{cc}{0} & {x<x_{1}^{*}} \\ {k / n} & {x_{k}^{*} \leq x<x_{k+1}^{*} \quad k=1,2, \cdots, n-1} \\ {1} & {x \geq x_{n}^{*}}\end{array}\right.\)
为总体\(X\)的经验分布函数
例子:
从一批标准重量为克的罐头中,随 机抽取8听:
8,-4,6 ,7, -2, 1, 0, 1测的误差
求总体\(X\)的经验分布函数
\(F_{n}(x)=\left\{\begin{array}{cc}{0} & {x<-7} \\ {1 / 8} & {-7 \leq x<-4} \\ {2 / 8} & {-4 \leq x<-2} \\ {3 / 8} & {-2 \leq x<0} \\ {4 / 8} & {0 \leq x<1} \\ {6 / 8} & {1 \leq x<6} \\ {7 / 8} & {6 \leq x<8} \\ {1} & {x \geq 8}\end{array}\right.\)
统计量:依赖于样本的函数
样本均值:\(\bar{X}=\bar{X}_{n}=\frac{1}{n} \sum_{i=1}^{n} X_{i}\)(总体样本)
(分组样本)样本均值的近似公式:\(\bar{x}=\frac{x_1f_1+\dots x_kf_k}{n} (n=\sum_{i=1}^{k}f_i)\)
\(f_i\)为第i组的频数,k为组数
样本k阶原点矩:\(X^{k}=\frac{1}{n} \sum_{i=1}^{n} X_{i}^{k}\)
单个正态总体分布下的样本均值分布:
\(\overline{\boldsymbol{X}}=\frac{1}{n} \sum_{i=1}^{n} X_{i} \sim N\left(\mu, \frac{\sigma^{2}}{n}\right)\)
证明:
\(X_{1}, X_{2}, \cdots, X_{n}\)独立同分布,\(E(X_i)=\mu\)


Survey sampling
\(\bullet\)What is survey sampling?(c.f.census survey)(c.f.:参考,查看,来源于拉丁语)
\(\bullet\)understanding the whole by a \(\underline{fraction}\)(i.e.a \(\underline{sample}\))
Population:
Q:What is the population to survey?(In some cases,it can be difficult to identify or determine)
N:population size
a sample of size n:a subgroup of n members(n<N)
Q:Which n members should be included in the sample?(i.e.how to produce a \(\underline{representative}\) sample)
quantity of interest:
\(x_i,i=1,2,3\cdots N\)(each labeled by an integer)
\(x_i\)can be \(\underline{numerical}\) or \(\underline{categorial}\)
Multivariate\((x_{i1},x_{i2}\cdots x_{ik}),i=1,2,3 \dots N\)
\(\underline{Definition : }\)(survey sampling)
A technique to obtain \(\underline{information}\) about a \(\underline{large}\) population by examining only