欧拉降幂（广义欧拉降幂）

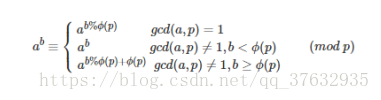
第一个要求a和p互质，第二个和第三个是广义欧拉降幂，不要求a和p互质，但要求b和的大小关系。

A^K^≡A^K%ϕ(m)+ϕ(m)^( mod m)          K>ϕ(m)                (1)

证明如下
1 若 (A,m)=1，根据欧拉定理 A^ϕ(m)≡1(mod m),即可轻易得证
2 若 (A,m)≠1,证明如下
设 K=a∗ϕ(m)+c a≥1,0≤c<ϕ(m)
那么欧拉降幂公式就是
A^K≡A^a∗ϕ(m)+c≡A^ϕ(m)+c( mod m) (2)

即 证
A^a∗ϕ(m)≡A^ϕ(m)(mod m)

即 证
A^2∗ϕ(m)≡A^ϕ(m)(mod m)

移项
A^ϕ(m)(Aϕ(m)−1)≡0(mod m)

即证
m|A^ϕ(m)(A^ϕ(m)−1)(3)
若有
(m(m,A^ϕ(m)),A)=1(4)

根据欧拉定理
A^ϕ(m)≡A^{k∗ϕ(m(m,Aϕ(m)))}≡(Aϕ^{(m(m,Aϕ(m)))})k≡1(mod (m(m,A^ϕ(m)))
其中k≥1
移项即得 m(m,A^ϕ(m))|(A^ϕ(m)−1)
同时乘 (m,A^ϕ(m))
即 m|(m,A^ϕ(m))∗(A^ϕ(m)−1)
即 m|A^ϕ(m)(A^ϕ(m)−1)
就是 式 3

所以证明 式子 4
(m(m,A^ϕ(m)),A)=1
就好了
进行素因子分解



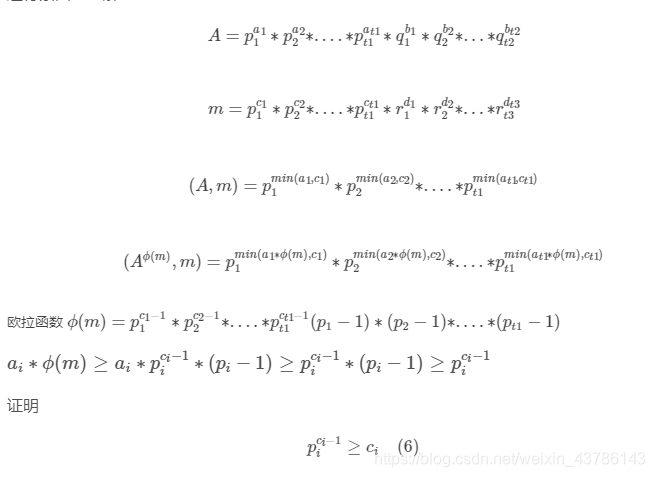
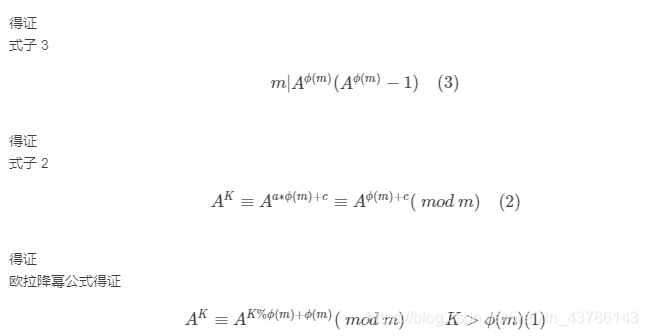
例题：求2⁽²(2⁽²(2^…)))) mod p的值
题解：

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
 
ll ph(ll x)
{
    ll res=x,a=x;
    for(ll i=2;i*i<=x;i++)
    {
        if(a%i==0)
        {
            res=res/i*(i-1);
            while(a%i==0) a/=i;
        }
    }
    if(a>1) res=res/a*(a-1);
    return res;
}
ll quick_pow(ll a,ll b,ll mod)
{
    ll ans=1;
    while(b)
    {
        if(b&1) ans=(ans*a)%mod;
        a=(a*a)%mod;
        b>>=1;
    }
    return ans;
}
ll f(ll p)
{
    if(p==1) return 0;
    ll k=ph(p);
    return quick_pow(2,f(k)+k,p);
}
 
int main()
{
    int T;
    scanf("%d",&T);
    while(T--)
    {
        ll p;scanf("%lld",&p);
        printf("%lld\n",f(p));
    }
    return 0;
}

#include <bits/stdc++.h>
#define ll __int64
#define mod 10000000007
using namespace std;
char a[1000006];
ll x,z;
ll quickpow(ll x,ll y,ll z)
{
    ll ans=1;
    while(y)
    {
        if(y&1)
            ans=ans*x%z;
        x=x*x%z;
        y>>=1;
    }
    return ans;
}
ll phi(ll n)
{
    ll i,rea=n;
    for(i=2;i*i<=n;i++)
    {
        if(n%i==0)
        {
            rea=rea-rea/i;
            while(n%i==0)
                n/=i;
         }
    }
    if(n>1)
        rea=rea-rea/n;
    return rea;
}
int main()
{
    while(scanf("%lld %s %lld",&x,a,&z)!=EOF)
    {
        ll len=strlen(a);
        ll p=phi(z);
        ll ans=0;
        for(ll i=0;i<len;i++)
            ans=(ans*10+a[i]-'0')%p;
        ans+=p;
        printf("%lld\n",quickpow(x,ans,z));
    }
    return 0;
}

#include<iostream>
#include<cstdio>
#include<cstring>
#define me(a,x) memset(a,x,sizeof(a))
using namespace std;
const int o_o=2e5+5;
const int mod=1e9+7;
const int oo=0x7fffffff;
const int sup=0x80000000;
typedef long long ll;
typedef unsigned long long ull;
ll euler(ll n){
	ll ans=n;
	for(ll i=2;i*i<=n;i++){
		if(n%i==0){
			ans=ans/i*(i-1);
			while(n%i==0)n/=i;
		}
	}
	if(n>1)
		ans=ans/n*(n-1);
	return ans;
}
ll ksm(ll a,ll b,ll MOD){
	ll ans=1;
	for(;b;b>>=1,a=a*a%MOD)
		if(b&1)
			ans=ans*a%MOD;
	return ans;
}
ll fun(ll t,ll k,ll MOD){
	if(MOD==1)
		return 0;
	ll MO=euler(MOD);
	ll p=fun(t+1,k,MO);
	return ksm(k,t*p+t*MO,MOD);
}
int main(){
	int t;for(cin>>t;t;t--){
		ll k,p;scnaf("%lld%lld",&k,&p);
		ll ans=fun(1,k,p);
		printf("%lld\n",ans);
	}
}