使用Logistic Regression方法对MNIST 数据集进行数字识别
问题描述
请设计下述算法,求解 MNIST 数据集上的Logistic Regression问题:
- 梯度下降法
- 随机梯度法
对于每种算法,请给出每步计算结果与最优解的距离以及每步计算结果在测试集上所对应的分类精度。此外,请讨论随机梯度法中Mini Batch大小对计算结果的影响。可参考:
http://deeplearning.net/tutorial/logreg.html
任务描述
MINIST数据集:
MNIST数据集由Yann LeCun搜集,是一个大型的手写体数字数据库,通常用于训练各种图像处理系统,也被广泛用于机器学习领域的训练和测试,是简单的灰色图像手写数字数据集。MNIST 是一个经典的手写数字数据集,其原始数据集包含 60000 个训练数据和 10000 个测试数据。每个数据的样本特征为 28×28 像素的灰度图(784 维向量),表示一个手写数字;标签为 0~9 中的一个数字。
任务分析:
读取数据后分析数据,并建立相关的预测模型,该模型读取一个样本数据后输出预测的标签。模型通过训练数据进行训练,并在测试数据上进行测试。训练期间采用梯度下降法、随机梯度法以及不同大小的mini batch进行训练,通过调整不同的参数达到较为理想的预测准确度,并根据实验结果分析不同算法的特征。
准备工作:数据读取与分析
首先下载对应的数据集到代码同一文件夹:
数据下载地址: http://yann.lecun.com/exdb/mnist/
将4个gz文件下载并移动到代码同一文件夹,在该网站可以看到该数据集的详细介绍,重点如下:
train-images-idx3-ubyte:训练集图像
train-labels-idx1-ubyte:训练集标签
t10k-images-idx3-ubyte:测试集图像
t10k-labels-idx1-ubyte:测试集标签
数据下载的网站里有数据的简单介绍,idx3和idx1数据略有不同,故读取时需要分类考虑:
# -*- coding: utf-8 -*-
"""
Created on Mon Dec 16 10:22:12 2019
@author: Ding
"""
import numpy as np
import matplotlib.pyplot as plt
import gzip as gz
#--------------------读取数据----------
#filename为文件名,kind为'data'或'lable'
def load_data(filename,kind):
with gz.open(filename, 'rb') as fo:
buf = fo.read()
index=0
if kind=='data':
#因为数据结构中前4行的数据类型都是32位整型,所以采用i格式,需要读取前4行数据,所以需要4个i
header = np.frombuffer(buf, '>i', 4, index)
index += header.size * header.itemsize
data = np.frombuffer(buf, '>B', header[1] * header[2] * header[3], index).reshape(header[1], -1)
elif kind=='lable':
#因为数据结构中前2行的数据类型都是32位整型,所以采用i格式,需要读取前2行数据,所以需要2个i
header=np.frombuffer(buf,'>i',2,0)
index+=header.size*header.itemsize
data = np.frombuffer(buf, '>B', header[1], index)
return data
#--------------------加载数据-------------------
X_train = load_data('train-images-idx3-ubyte.gz','data') # 训练数据集的样本特征
y_train = load_data('train-labels-idx1-ubyte.gz','lable') # 训练数据集的标签
X_test = load_data('t10k-images-idx3-ubyte.gz','data') # 测试数据集的样本特征
y_test = load_data('t10k-labels-idx1-ubyte.gz','lable') # 测试数据集的标签
#---------查看数据的格式-------------
print('Train data shape:')
print(X_train.shape, y_train.shape)
print('Test data shape:')
print(X_test.shape, y_test.shape)
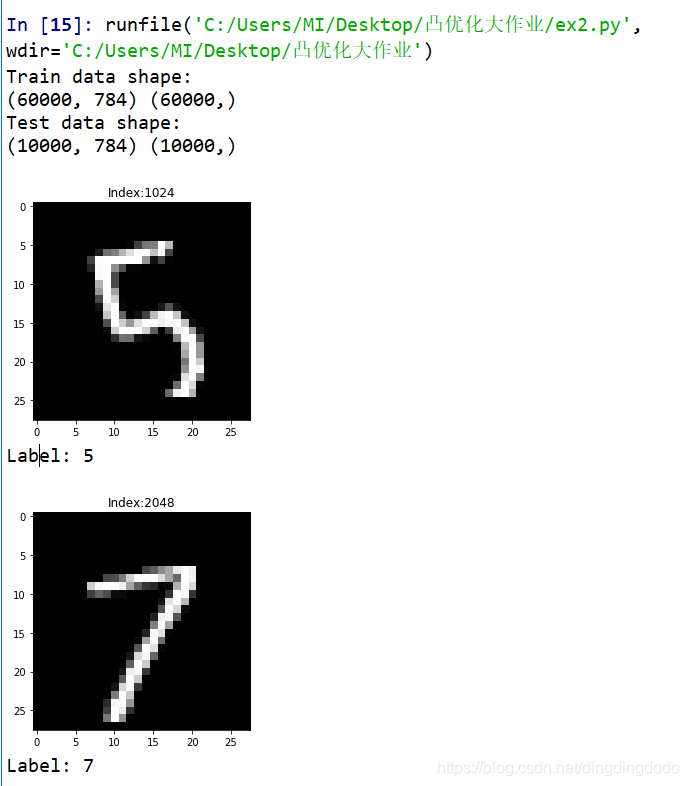
#--------------查看几个数据-----------
index_1 = 1024
plt.imshow(np.reshape(X_train[index_1], (28, 28)), cmap='gray')
plt.title('Index:{}'.format(index_1))
plt.show()
print('Label: {}'.format(y_train[index_1]))
index_2=2048
plt.imshow(np.reshape(X_train[index_2], (28, 28)), cmap='gray')
plt.title('Index:{}'.format(index_2))
plt.show()
print('Label: {}'.format(y_train[index_2]))
读取数据后存储在x_train,y_train,x_test,y_test中,查看了其中的两个数据,看一下数据的情况:
所以可以看出train数据中有60000个,test数据中有10000,data中数据为手写数字图像,在示例中我们可以看到图像还是较易识别的。
建立Logistic Regression模型
该问题是一个多分类问题,因此使用Logistic Regression时激活函数选用Softmax函数:
该函数可以将输入映射为
之间的实数,同时具有归一化的特征,因此与概率可以对应,易与分类任务对应。
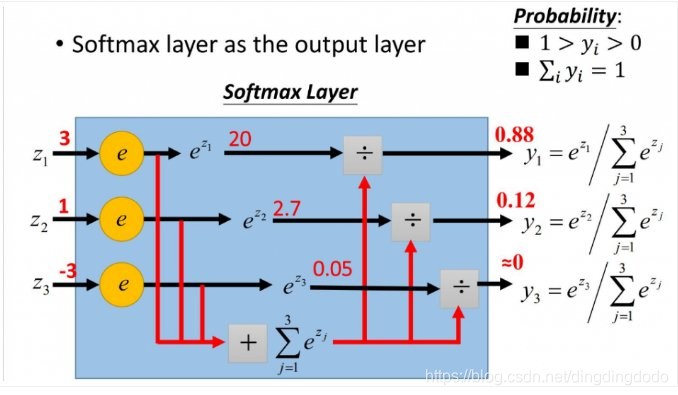 故根据这个思路,建立Logistic Regression模型。
故根据这个思路,建立Logistic Regression模型。
定义损失函数:
在使用softmax函数时,我们普遍采用交叉熵作为损失函数:
其中
表示期望的概率分布,
表示实际的概率分布,
表示交叉熵。
交叉熵刻画的是实际输出概率和期望输出概率的距离,交叉熵的值越小,则两个概率分布越接近,即实际与期望差距越小 。交叉熵可以反映出隐藏在输出结果背后的更深的错误率表现出来。
因此,在softmax模型中,用交叉熵函数表示的损失函数为:
其中
表示样本标签,表示是否属于类型
,
为属于类型c的概率
由于我们使用了softmax函数的输出作为概率,故在此处 可以视为
进一步简化,每一次的标签实际上除了真实值处,其余均为0,故对于单数据而言:
实际上我们是希望通过训练得到一个
,再对该函数的结果进行softmax,使该线性函数能够将x映射到正确的标签,所以训练目标为找到最优的W和b
故对于样本
,损失函数为
求梯度过程非常复杂,在此调用了已推导过的结论:
引用自: https://www.jianshu.com/p/4670c174eb0d https://www.jianshu.com/p/6e405cecd609
单样本损失函数梯度如下:
在此多样本情况直接相加即可。
需要注意的是,我们最终的预测结果为softmax函数的结果向量中最大的元素的下标。
同时,我们可以通过将训练后的模型进行测验,从而在测试集上得到正确率accurate_rate,以检验模型效果,通过调整参数等操作使正确率尽可以高。
故很容易使用python实现Logistic Regression模型的基本框架:
#-------------------------------定义常量-----------------
x_dim = 28 * 28 #data shape,28*28
y_dim = 10 #output shape,10*1
W_dim = (y_dim, x_dim) # 矩阵W
b_dim = y_dim #index b
#----------------------定义logic regression中的必要函数------
# Softmax函数
def softmax(x):
"""
输入向量x,输出其经softmax变换后的向量
"""
return np.exp(x) / np.exp(x).sum()
#Loss函数
#L=-log(Si(yi)),yi为预测值
def loss(W, b, x, y):
"""
W, b为当前的权重和偏置参数,x,y为样本数据和该样本对应的标签
"""
return -np.log(softmax(np.dot(W,x) + b)[y]) # 预测值与标签相同的概率
#单样本损失函数梯度
#按照公式很容易写出来
def L_Gra(W, b, x, y):
"""
W, b为当前的权重和偏置参数,x,y为样本数据和该样本对应的标签
"""
#初始化
W_G = np.zeros(W.shape)
b_G = np.zeros(b.shape)
S = softmax(np.dot(W,x) + b)
W_row=W.shape[0]
W_column=W.shape[1]
b_column=b.shape[0]
#对Wij和bi分别求梯度
for i in range(W_row):
for j in range(W_column):
W_G[i][j]=(S[i] - 1) * x[j] if y==i else S[i]*x[j]
for i in range(b_column):
b_G[i]=S[i]-1 if y==i else S[i]
#返回W和b的梯度
return W_G, b_G
#检验模型在测试集上的正确率
def test_accurate(W, b, X_test, y_test):
num = len(X_test)
#results中保存测试结果,正确则添加一个1,错误则添加一个0
results = []
for i in range(num):
#检验softmax(W*x+b)中最大的元素的下标是否为y,若是则预测正确
y_i = np.dot(W,X_test[i])+ b
res=1 if softmax(y_i).argmax()==y_test[i] else 0
results.append(res)
accurate_rate=np.mean(results)
return accurate_rate
优化方法:梯度下降
建立好Logistic Regression模型后,可以对该模型进行优化,以得到较好的参数。
在此仅设置一个mini_batch算法,因为在mini_batch算法中,当size为1时则为随机梯度下降,当size为all时则为梯度下降,因此可以通过调整size的大小实现不同的梯度下降策略。
批量梯度下降、随机梯度下降、mini-batch梯度下降算法简介:
- 批量梯度下降每次迭代时使用所有样本进行梯度的更新,每次更新的梯度就是所有的梯度和,故当目标函数为凸函数时,一定可以达到全局最优,但是由于每次需要使用所有样本,因此训练过程非常慢,并且当样本非常大时将耗费巨大的计算资源和时间
- 随机梯度下降每次迭代随机使用一个样本,因此每轮迭代将非常快,但是由于单个样本不能代表全局样本的趋势,故可能无法收敛,同时使最优解的准确度下降,但由于其速度上有非常好的优势,故现在大多数样本较大的机器学习采用该策略。随机梯度下降通常来说使得参数在大体上趋向于最优的,通常会达到最优解附近
- mini-batch梯度下降则是上述两种方法的折中,每次迭代采用batch-size个样本数据来对参数进行更新,故在该方法中size的选择通常是较为重要的,选择较好的size可以发挥批量梯度下降和随机梯度下降的优势,在较快的速度内完成迭代且最终有着不错的收敛效果。实际上当size选择为1的时候就是随机梯度下降,当size为data-size的时候则为批量梯度下降
- 需要注意的是,通过查看训练数据可以得知数据具有非常好的随机性,即不具备局部性的特点(并非是一批数据为1的数据聚集在一起,一批数据为2的样本聚集在一起,而是非常好的分散随机分布),故在此可以直接遍历每一个batch数据即可,不需要每次选取随机以避免局部性的特点
设置不同的size时对应的梯度只需要将所取的样本求和即可。
故写代码时直接写一个具有泛化的mini-batch,通过修改步长即可完成三种方法的实现和比较。
# mini-batch随机梯度下降
def mini_batch(batch_size,alpha,epoches):
"""
batch_size为batch的尺寸,alpha为步长,epochsnum为epoch的数量,即直接决定了训练的次数
"""
accurate_rates = [] # 记录每次迭代的正确率 accurate_rate
iters_W = [] # 记录每次迭代的 W
iters_b = [] # 记录每次迭代的 b
W = np.zeros(W_dim)
b = np.zeros(b_dim)
#根据batch_size的尺寸将原样本和标签分批后
#初始化
x_batches=np.zeros(((int(X_train.shape[0]/batch_size),batch_size, 784)))
y_batches=np.zeros(((int(X_train.shape[0]/batch_size),batch_size)))
batches_num = int(X_train.shape[0]/batch_size)
#分批
for i in range(0,X_train.shape[0],batch_size):
x_batches[int(i/batch_size)]=X_train[i:i+batch_size]
y_batches[int(i/batch_size)]=y_train[i:i+batch_size]
print('Start training...')
start = time.time() # 开始计时
#print(start)
for epoch in range(epoches): #对所有样本循环一遍为一个epoch
for i in range(batches_num): #对一个batch循环一遍为一个iteration
#初始化梯度
W_gradients = np.zeros(W_dim)
b_gradients = np.zeros(b_dim)
x_batch,y_batch= x_batches[i],y_batches[i]
#求一个batch的梯度,实际上对一个batch中的样本梯度求和然后平均即可
for j in range(batch_size):
W_g,b_g = L_Gra(W, b,x_batch[j], y_batch[j])
W_gradients += W_g
b_gradients += b_g
W_gradients /= batch_size
b_gradients /= batch_size
#进行梯度下降
W -= alpha * W_gradients
b -= alpha * b_gradients
#把迭代后的精度、W、b都加入到相应的数组,便于之后分析和绘制图像
#当size较小时采用每100个ite记录一次
#当size较大时每次ite记录一次
if i%100==0:
accurate_rates.append(test_accurate(W, b, X_test, y_test))
#accurate_rates.append(test_accurate(W, b, X_test, y_test))
iters_W.append(W.copy())
iters_b.append(b.copy())
end = time.time() # 结束计时
#print(end)
time_cost=(end - start)
return W,b,time_cost, accurate_rates, iters_W, iters_b
模型整合
优化方法完成后,便可以对整个Logistic Regression模型进行整合,对输入的参数进行调试并以可视化的方式查看效果,包括随着迭代的进行模型在测试集上的精度变化图、W和b的收敛效果图(即每次迭代时每步计算结果与最优解的距离):
#-------------模型的主函数-------------------
def run(alpha,batch_size,epochs_num):
#将参数带入并训练,将训练结果存储到下列变量中
#W和b表示最优的W和b,time_cost表示训练该模型时间
#accuracys,W_s,b_s分别表示accuracy,W,b随着迭代次数的变化的变化
W,b,time_cost,accuracys,W_s,b_s = mini_batch(batch_size,alpha,epochs_num)
#求W和b与最优解的距离,用二阶范数表示距离
iterations=len(W_s)
dis_W=[]
dis_b=[]
#test=b_s[:10]
#print(test)
#起初b的变化是直线,仔细分析数据后发现b值确实为非常小的值,图像中难以显示
for i in range(iterations):
dis_W.append(np.linalg.norm(W_s[i] - W))
dis_b.append(np.linalg.norm(b_s[i] - b))
#--------简单介绍------
print("the parameters is: step length alpah:{}; batch size:{}; Epoches:{}".format(alpha, batch_size, epochs_num))
print("Result: accuracy:{:.2%},time cost:{:.2f}".format(accuracys[-1],time_cost))
#----------------作图--------------
#精确度随迭代次数的变化
plt.title('The Model accuracy variation chart ')
plt.xlabel('Iterations')
plt.ylabel('Accuracy')
plt.plot(accuracys,'m')
plt.grid()
plt.show()
#W和b距最优解的距离随迭代次数的变化
plt.title('The distance from the optimal solution')
plt.xlabel('Iterations')
plt.ylabel('Distance')
plt.plot(dis_W,'r', label='distance between W and W*')
plt.plot(dis_b,'g',label='distance between b and b*')
plt.legend()
plt.grid()
plt.show()
#print(W,b)
#----------参数输入---------------
alpha = 1e-5
batch_size = 1000
epochs_num = 1
# 运行函数
run(alpha,batch_size,epochs_num)
至此,整个模型完成,可以输入不同参数进行调整
结果分析
调整不同的batch-size和步长 $\alpha $ 以及epoch(每个样本的使用次数),查看精度以及训练时间、迭代次数等情况:
- 步长
的选取:
在batch-size=1000时训练较快且效果较好,因此我固定batch-size为1000,调整步长以找到较好的步长。通过调整 分别为 , , 等值,发现 和 时效果均非常不错,所以之后我均在二者之间择最优选取步长,当然这是很强的经验性,但在之后测试的效果还不错
batch-size为1000,epoch=1时的不同 的效果
| 步长α | 一个epoch后的训练效果 | 精度 | 训练时间 |
|---|---|---|---|
 |
16.41s | ||
 |
14.5s | ||
 |
13.1s |
故之后均选取了 或 作为步长
-
探索不同batch-size对结果的影响:
-
当 batch-size=60000 时,此时等价于全批量梯度下降:
| 步长α | 样本使用次数epochs | accuracy chart | distance from the optimal solution | accuracy | time |
|---|---|---|---|---|---|
| 100 |  |
![]](https://img-blog.csdnimg.cn/20200205154709519.png?x-oss-process=image/watermark,type_ZmFuZ3poZW5naGVpdGk,shadow_10,text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L2RpbmdkaW5nZG9kbw==,size_16,color_FFFFFF,t_70) |
285s | ||
| 100 |  |
 |
288s | ||
| 1000 |  |
 |
2950s | ||
| 1000 |  |
 |
2955s |
显然,对这个结果分析,我们可知当 时波动性太大,效果太差,故设置 效果非常好
当epoch为100,即将整体样本训练100次时,训练精度为 ;当epoch为 1000时,即将整体样本训练1000次时,训练精度 ,已经达到非常优秀的效果,故不再扩大epoch以获得更大的精度,实际上效果不会有明显的提升
通过分析图像可知,实际上在很少的迭代后便达到了一个不错的解
- 当batch为2000时,实验结果如下:
| 步长α | 样本使用次数epochs | accuracy chart | distance from the optimal solution | accuracy | time |
|---|---|---|---|---|---|
| 10 |  |
 |
79s | ||
| 100 |  |
 |
798s |
很显然经过10个epoch训练后即达到了非常可观的精度,且训练时间也较短
经过100个epoch训练基本达到了最优,精度为 ,还是非常可观的
-
当batch为100时,结果如下:(由于batch-size比较小,迭代太多,故每100次迭代计算一次accuracy)
| 步长α | 样本使用次数epochs | accuracy chart | distance from the optimal solution | accuracy | time |
|---|---|---|---|---|---|
| 10 |  |
 |
82s | ||
| 10 |  |
 |
83s |
此时选取步长为 时波动性非常大,故选取 较好,此时10个epoch已经达到最优,准确度为
- 当batch-size为10时,结果如下:(由于batch-size比较小,迭代太多,故每100次迭代计算一次accuracy)
| 步长α | 样本使用次数epochs | accuracy chart | distance from the optimal solution | accuracy | time |
|---|---|---|---|---|---|
| 1 |  |
 |
16.6s | ||
| 10 |  |
 |
146s |
- 当batch-size为1时,等价于随机梯度下降,结果如下:(由于batch-size比较小,迭代太多,故每100次迭代计算一次accuracy)
| 步长α | 样本使用次数epochs | accuracy chart | distance from the optimal solution | accuracy | time |
|---|---|---|---|---|---|
| 1 |  |
 |
169s |
总体结果分析
对比上述结果,当batch-size选取为2000和100以及10时均可以在可接受训练时间内达到一个很不错的效果, 左右,效果非常理想。通常来说,会通过结果来测试不同size的影响,在时间和效果上取折中方案,随机梯度下降非常快但是总体效果并不是最好,因为会在最优解附近波动,通过适当加大size可以在较短时间内获得较为稳定的最优解
模型部分解释
- mini-batch直接循环遍历了样本,未采用每一步随机采取样本,原因:查看训练数据可知数据整体的分布是较为分散的,即并非同一类样本全部聚集在一块,因此直接遍历不会因此陷入局部最优的情况,故采用该方式即可
- 步长 的选取,需要知道的是当batch-size较小的时候,模型最终可能在最优解附近频繁跳转而不收敛,因此当batch-size较小时设置步长较小比较好
- 当batch-size较大时,每次迭代均会计算并保留其精确度,当batch-size比较小时,每100次迭代会计算并保留一次精确度,避免过多时间花费在求精确度上
- 比较不同算法时不应该去比较相同迭代次数情况下效果如何,而应该比较相同epoch或者相同训练时间情况下不同参数的效果如何,以选择在时间和精度上均符合预期的参数作为最优