tensorflow学习笔记——常见的优化器

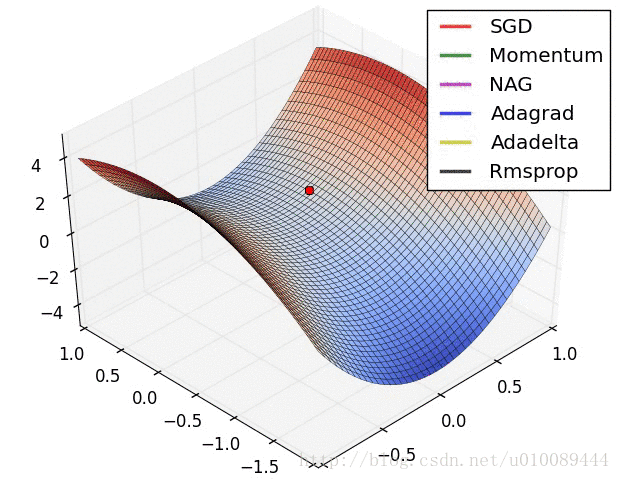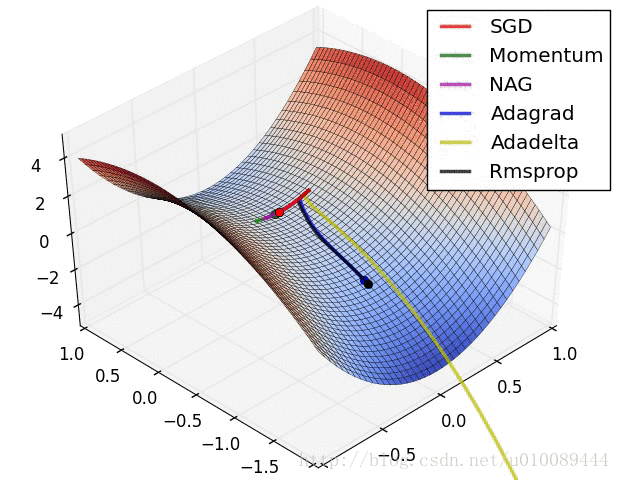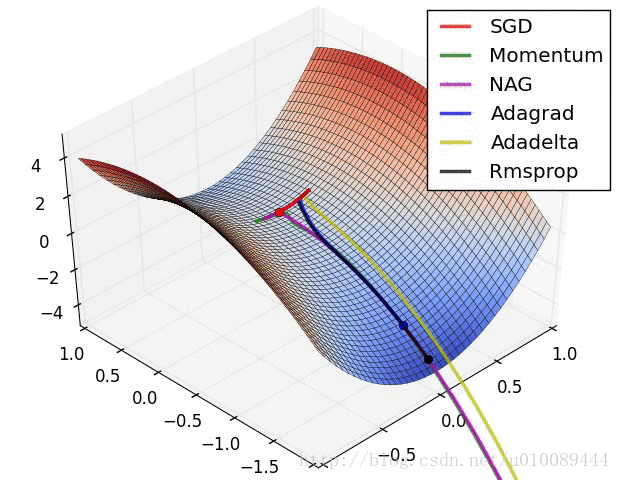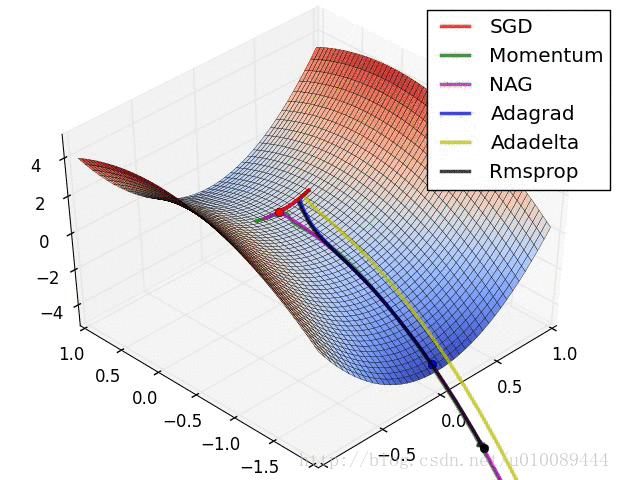
SGD：

在最小化损失函数中，最常用的就是梯度下降法。梯度下降法主要有三种变体：

1.Vanilla 梯度下降：在 Vanilla 梯度下降（也称作批梯度下降）中，在每个循环中计算整个训练集的损失函数的梯度。该方法可能很慢并且难以处理非常大的数据集。该方法能保证收敛到凸损失函数的全局最小值，但对于非凸损失函数可能会稳定在局部极小值处。

2.随机梯度下降：在随机梯度下降中，一次提供一个训练样本用于更新权重和偏置，从而使损失函数的梯度减小，然后再转向下一个训练样本。整个过程重复了若干个循环。由于每次更新一次，所以它比 Vanilla 快，但由于频繁更新，所以损失函数值的方差会比较大。

3.小批量梯度下降：该方法结合了前两者的优点，利用一批训练样本来更新参数。一般会使用这种方法。

这里我们主要讲随机梯度下降法（SGD）：

$W=W-\eta \cdot \bigtriangledown _{W}J$

W：要训练的参数；
J(W)代价函数；
$\bigtriangledown _{W}J$ ：代价函数的梯度；
$\eta$ ：学习率。

Momentum：

$v_{t}=\gamma v_{t-1}+\eta \bigtriangledown _{W}J(W)$

$W=W-v_{t}$

$\gamma$ :动力，通常设为0.9。

加入动力既可以加快收敛速度，也可以一定程度避免局部最小点（当然也可能冲出全局最小点）。

NAG：

$v_{t}=\gamma v_{t-1}+\eta \bigtriangledown _{W}J(W-\gamma v_{t-1})$

$W=W-v_{t}$

在Momentum中小球会盲目跟从下坡的梯度，我们这里对此进行改进，加入了 $\gamma v_{t-1}$ 用来修改W的值。计算W- $\gamma v_{t-1}$ 可以表示小球下一个位置在哪里，提取估计下一个位置梯度，使用到当前位置这种预期的更新可以避免我们走的太快。（还不太懂，只知道在梯度较大时候适当抑制收敛速度）

Adagrad：

$W_{t+1}=W_{t}-\frac{\eta }{\sqrt{\sum_{t^{'}=1}^{t}(g_{t^{'},i})^{2}+\varepsilon }}\cdot g_{t}$

i：第i个分类；
t：代表出现次数；
$\varepsilon$ ：避免分母为0，一般取e-8；
$\eta$ ：一般取0.01；
$g_{t}=\bigtriangledown _{W}J(W_{i})$ 。

它比较适合稀疏数据集。对比较少见的数据给予较大的学习率取调整参数，对于较大的数据集给予较小1学习率取调整参数。（比如一个图片数据集里有1000张猫的照片但只有100张狗的照片）

其优点在于不需要人为调节学习率，它可以自动调节。缺点在于随着迭代次数增多，学习率会越来越低直至趋近于0。

RMSprop：

RMS（Root Mean Square）是均方根的缩写。它借鉴了一些Adagrad的思想，公式如下：

$W_{t+1}=W_{t}-\frac{\eta }{\sqrt{E[g^{2}]_{t}+\varepsilon }}\cdot g_{t}$

$E[g^{2}]_{t}=\gamma E[g^{2}]_{t-1}+(1-\gamma )g^{2}_{t}$

$E[g^{2}]_{t}$ ：前t次的梯度平方的平均值。

与Adagrad不同的是，RMSprop不会出现学习率越来越低的问题，而且仍能够自己调节学习率，可以有一个比较好的效果。（疑问：既然求均值，那自我调节学习率有什么意义，从公式看梯度越大分母越大，学习速度越慢？）

Adadelta：

$\Delta W=-\frac{\eta }{\sqrt{E[g^{2}]_{t}+\varepsilon }}\cdot g_{t}$

$\Delta W=-\frac{\eta }{RMS[g^{2}]_{t}}\cdot g_{t}$

$W_{t+1}=W_{t}-\frac{RMS[\Delta W]_{t-1}}{RMS[g]_{t}}$

不需要设置默认的学习率。

上面各优化器代码如下：

train_step = tf.train.GradientDescentOptimizer(0.2).minimize(loss)
train_step = tf.train.MomentumOptimizer(0.1,0.9,use_nesterov=True).minimize(loss) 
#use_nesterov为True时为NAG,False时为.Momentum，默认为False
train_step = tf.train.AdagradOptimizer(0.1).minimize(loss)
train_step = tf.train.RMSPropOptimizer(0.01).minimize(loss)
train_step = tf.train.AdamOptimizer(1e-2).minimize(loss)
train_step = tf.train.AdadeltaOptimizer(1).minimize(loss)

以上只填写了最基础的参数，其他参数可根据需要自己添加。不同优化器对应不同网络，不同学习率，不同批量大小时效果差别较大，具体最好的组合还得自己多种尝试。

下面是网上找到2张动图，可以看一下这些优化器的训练过程。不过每个优化器适用的情况不同，没有绝对的优劣性。

红鱼鱼

发布了33 篇原创文章 · 获赞 148 · 访问量 1万+

私信关注