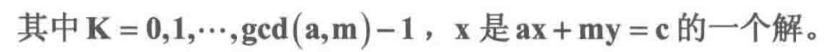扩展欧几里得算法后续 ax+by=c求解 同余式 逆元

模板

扩展欧几里得算法应用

通过exgcd算法，我们可以求出ax+by=gcd(a,b)的一组解，然后通过
$\begin{cases} x'=x+\frac{b}{gcd(a,b)}*K\\ y'=y-\frac{a}{gcd(a,b)}*K(K为任意整数)\\ \end{cases}$
就可以得到所有的解
$*$ax+by=c$有解的充要条件是 $c\%gcd(a,b)==0$$
所以 a、b互素,等价于存在整数x、y,使得ax+by=1

求除了 $ax+by=c$的一组解 $(\frac{cx_0}{gcd},\frac{cy_0}{gcd})$ ,用下面的公式得到全部的解
$\begin{cases}x'=x+\frac{b}{gcd}*K=\frac{cx_0}{gcd}+\frac{b}{gcd}*K\\ y'=y-\frac{a}{gcd}*K=\frac{cy_0}{gcd}+\frac{a}{gcd}*K \end{cases}$

模算数

$(a+b)\space mod\space m=((a \space mod\space m)+(b \space mod\space m))\space mod \space m$
$(a-b)\space mod\space m=((a \space mod\space m)-(b \space mod\space m)+m)\space mod \space m$
$(a*b)\space mod\space m=((a \space mod\space m)*(b \space mod\space m))\space mod \space m$

同余式 $ax\equiv c(mod\space m)$的求解

同余式 $a\equiv b \space (mod \space m)$代表 $(a-b)\%m=0$
那么 $ax\equiv c(mod\space m)$就等价于 $(ax-c)\%m=0$,因此 $ax-c=my$,得到 $ax+my=c$，当且仅当 $c\%gcd(a,m)=0$时才有解，然后由公式 $\begin{cases} x'=x+\frac{m}{gcd(a,m)}*K\\ y'=y-\frac{a}{gcd(a,m)}*K(K为任意整数)\\ \end{cases}$
其中K可以取到任意值，但是我们只关注x，并且要x的值要模m后不同，那么K=0，1，2，…，gcd(a,m)-1.就是K的全部取值，剩下的模m后会重复，所以可以舍弃

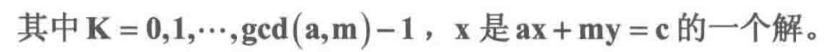
逆元的求解和 $(b/a)\%m$的运算

逆元（特指乘法逆元），假设a,b,m是整数，其中m>1，且有 $ab\equiv1(mod\space m)$成立，那么就说a,b互为模m的逆元，也记作 $a\equiv \frac{1}{b}(mod\space m)$, $b\equiv \frac{1}{a}(mod\space m)$.就是说，a，b的成绩模m结果是1,那么a,b,互为模m的逆元
问题：假设a,m是整数，求a%m的逆元(b%m=0的情况下)
逆元的用处： $(b*a)\%m=((a\%m)*(b\%m))\%m$,那么 $(b/a)\%m$呢？ $(b/a)\%m!=((b\%m)*(a\%m))\%m$,也不等于 $((b\%m)\%a)$,这是可以用逆元计算 $((b/a)\%m)$，通过找到a的逆元x，把 $(b/a)\%m$变成 $(b*x)\%m$，这种做法可以使b预先对m取模，再进行计算，结果不变

所以对于求a关于m的逆元，首先得gcd(a,m)=1，才有逆元，否则逆元不存在，然后就是用扩展欧几里得算法求解 $ax+my=1$，求除了一组x,y后，使用 $(x\%m+m)\%m$求出a的逆元
代码：

int inverse(int a,int m){
	int x,y;
	int t=exGCD(a,m,x,y);
	return (x%m+m)%m;  //多加了个m是为了确保x%m+m是正数
}

另外，如果m是素数，且a不是m的倍数，那么可以不通过扩展欧几里得算法，直接使用费马小定理来得到a的逆元
费马小定理:m是素数，a是任意整数，且不满足 $a\equiv0(mod\space m)$,那么 $a^{m-1}\equiv1(mod\space m)$,所以 $a^{m-2}\%m$就是a模m的逆元，这个可以通过快速幂运算很快求出来

//快速幂  (a^b)%m
ll qpow(ll a,ll b,ll m){
	ll ans=1,res=a;
	while(b){
		if(b&1) ans=ans*res%m;  //值
		res=res*res%m;  //基底
		b>>=1;
	}
	return ans;
}

那么如果gcd(a,m)!=1，该如何求解？这是扩展欧几里得和费马小定理均失效，但是 $(b/a)\%m$还是存在的，设 $(b/a)\%m=x$,那么 $(b/a)=km+x\Rightarrow b=kma+ax\Rightarrow (b\%am)=ax\Rightarrow (b\%am)/a=x$,所以 $(b/a)\%m=(b\%am)/a$
因此，在a,m不互素的情况下，可以使用所以 $(b/a)\%m=(b\%am)/a$来计算，但是a*m可能过大会溢出，所以还是优先采用扩展欧几里得和费马小定理，最后再使用这个方法