深度学习笔记------神经网络

神经网络

与生物学中的神经网络相似，其是一个网状的结构，其组成的基本单元是一个个的神经元模型，这些小的单元模型可以处理传入的部分数据，并根据相应的结果来产生相应数据与信号，配合其它的神经元模型协同工作。

层级结构

除此之外，这里的神经网络是一个层级结构，整体分为输入层，输出层与隐藏层。
输入层：输入层是数据传入的入口，这一层不包含计算只用于传入数据。
输出层：输出层是数据输出的出口，但是这一层包含计算，只含有输入层与输出层便可构成可用的模型了。
隐藏层：夹在输出层与输入层之间有若干的隐藏层，隐藏这个词给人以一种黑箱的感觉，其中实现了相关的运算，层数与相关实现是比较灵活的可以自定义。

相邻的层中除输出层与输入层外，前一层的输出是下一层的输入。各层的神经元数量可能不同，特别是在隐藏层中相关的实现可以非常灵活。

多层模型

在神经网络中我们重点在于多层模型上，这里的多层是指至少要有隐藏层。

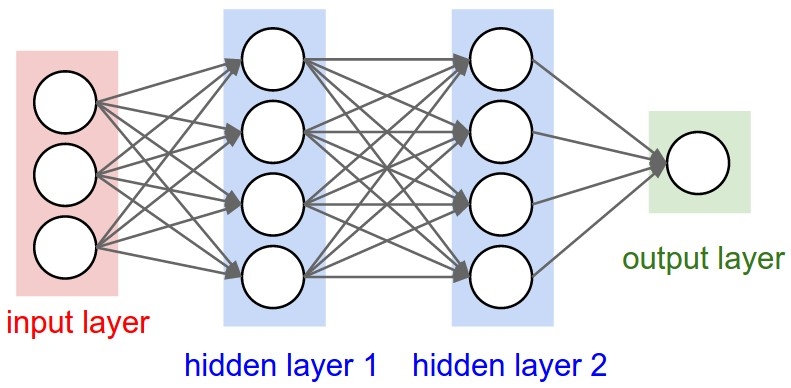
而模型的重点在于各神经元间连线的权值上，这些权值实际定义了相关层级数据到下一层级的线性运算，是这个模型要"学习"的重点。除了权值之外还有阈值，也可以叫偏置，在线性回归 $y=w_1x_1+...+w_nx_n+b$中，这个偏置的b就是相应的阈值，它调节了产生不同类型激励信号的难易程度（正值还是负值）。相应的属性进行扩展加上一个固定为1的属性，同时对相应权值也进行扩展，将对应的 $w_{n+1}$用于描述b，可以保持形式的一致性，将模型的重点统一到这些权值上。

激活函数

先看看一个例子：在对应模型的输入为 $X$（输入层）
第一层数据的处理为 $H_1=XW_{h1}+b_{h1}$
第二层为 $H_2=H_1W_{h2}+b_{h2}$
$....$
第n层为 $H_n=H_{n-1}W_{h_{n-1}}+b_{h_{n-1}}$
输出层为 $O=H_{n}W_{o}+b_{o}$
将 $b$合并入 $W$中，对应输入到输出为：
$O=XW_{h1}...W_{h_{n-1}}W_{o}，而$ $W_{h1}...W_{h_{n-1}}W_{o}$对应仍是一个线性变换。

仅通过线性变换来进行数据映射，对于有非线性特点数据无法很好的拟合，所以我们需要激活函数来为模型提供一些非线性的元素，以提高其对于数据的学习能力。

ReLU函数

$ReLU(x)=\max(x,0)$

运算简单，在运行中的运算成本低。在梯度下降中由于没有其他复杂形式函数的干扰往往效率更高。

Sigmoid函数

$Sigmoid(x)=\frac{1}{1+e^{-x}}$

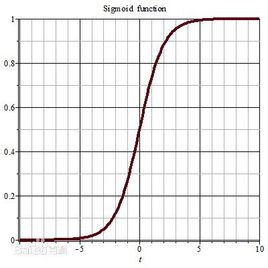
Sigmoid函数可以将元素的值都映射到(0,1)之间，这是该函数的一个特性，当x趋于0时其函数接近与线性变换。其对应的导数为：
$S'(x)=\frac{e^{-x}}{(1+e^{-x})^2}=S(x)S(1-x)$

Tanh函数

$Tanh(x)=\frac{1-e^{-2x}}{1+e^{-2x}}$

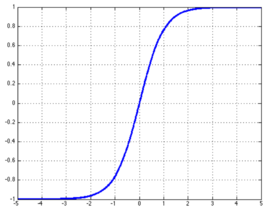
Tanh函数可以将元素的值都映射到(-1,1)之间，当x趋于0时其函数接近与线性变换，并且其函数关于原点对称。其对应的导数为：
$T'(x)=1-T^2(x)$

模型计算

正向传播

正向传播的过程是神经网络沿着从输入层到输出层的顺序，依次进行中间遍历的计算并存储相应的中间变量（包含输出值），而具体计算的过程依据之前的模型定义逐层进行，以下图为例（激活函数选用Sigmoid函数）

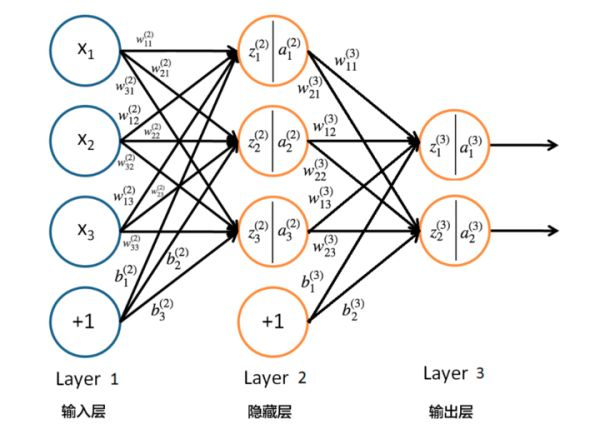
首先 $x_1,x_2,x_3$皆为输入数据，对应到隐藏层的权值为 $w$。
由输入层到隐藏层有：
$z_1^{1}=x_1w_{11}^{1}+x_2w_{12}^{1}+x_3w_{13}^{1}+b_1^{1}$
$z_2^{1}=x_1w_{21}^{1}+x_2w_{22}^{1}+x_3w_{23}^{1}+b_2^{1}$
$z_3^{1}=x_1w_{31}^{1}+x_2w_{32}^{1}+x_3w_{33}^{1}+b_3^{1}$
相应的存储中间变量

之后是在隐藏层中进行激活运算：
$a_1^1=sigmoid(z_1^{1})$
$a_2^1=sigmoid(z_2^{1})$
$a_3^1=sigmoid(z_3^{1})$
同样要存储相关的中间变量

由隐藏层到输出层有：
$z_1^{2}=a_1^1w_{11}^{2}+a_2^1w_{12}^{2}+a_3^1w_{13}^{2}+b_1^{2}$
$z_2^{2}=a_1^1w_{21}^{2}+a_2^1w_{22}^{2}+a_3^1w_{23}^{2}+b_2^{2}$
相应的存储中间变量

之后是在输出层中进行激活运算：
$a_1^2=sigmoid(z_1^{2})$
$a_2^2=sigmoid(z_2^{2})$
得到相应的输出，也存入中间变量。
于是由输入到输出完成了相应结果的计算，并且记录了相应的中间变量。对应含更多隐藏层时运算也是一样，当然在不同层间可能含有不同的激活函数。
最终还可以加一个softmax函数获得最终的结果 $\hat y$，根据相应的代价函数 $H(\hat y,y)$来得到最终的一个误差评估。

这里的上方标号1，2为标记不是平方

反向传播

反向传播的方向是由输出到输入，计算的是相关参数的梯度（主要是那些权值与偏置的梯度），在计算中会使用到之前正向传播的许多中间变量，计算的这些梯度将用于模型训练时的迭代优化计算。

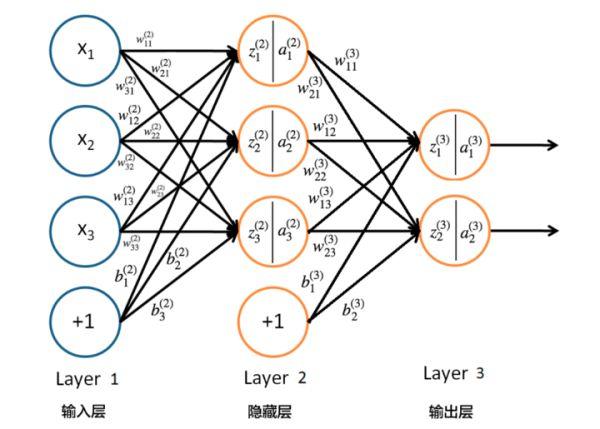
梯度的计算主要是使用了链式法则，对应例子还是以上图为例。
由后向前首先是对 $w^{2}_i$与 $b^2_i$参数的计算，最终目的是关于代价函数 $H(\hat y,y)$的。以 $w_{11}^{2}$为例：
通过 $z_1^{2}=a_1^1w_{11}^{2}+a_2^1w_{12}^{2}+a_3^1w_{13}^{2}+b_1^{2}$
$\hat y_1=a_1^2=sigmoid(z_1^{2})$
再到 $H(\hat y,y)$来影响最终结果。
相应的梯度有： $\frac{\partial H(\hat y,y)}{\partial w_{11}^{2}}=\frac{\partial H(\hat y,y)}{\partial \hat y_1}\frac{\partial \hat y_1}{\partial z_1^{2}}\frac{\partial z_1^{2}}{\partial w_{11}^{2}}$
其中 $\frac{\partial z_1^{2}}{\partial w_{11}^{2}}=a_1^1$， $\frac{\partial \hat y_1}{\partial z_1^{2}}=sigmoid(z_1^{2})sigmoid(1-z_1^{2})$，相应的代价函数对应求导即可，这里不在赘述。
最终获得相应的梯度有 $g=\frac{\partial H(\hat y,y)}{\partial w_{11}^{2}}$，于是加上相应的学习率 $\eta$有 $w_{11}^{2}=w_{11}^{2}+\eta g$，从而可以进行相应的迭代梯度下降。

同理对于相应的偏置参数b也类似有：
通过 $z_1^{2}=a_1^1w_{11}^{2}+a_2^1w_{12}^{2}+a_3^1w_{13}^{2}+b_1^{2}$
$\hat y_1=a_1^2=sigmoid(z_1^{2})$
再到 $H(\hat y,y)$来影响最终结果。
相应的梯度有： $g=\frac{\partial H(\hat y,y)}{\partial b_1^{2}}=\frac{\partial H(\hat y,y)}{\partial \hat y_1}\frac{\partial \hat y_1}{\partial z_1^{2}}\frac{\partial z_1^{2}}{\partial b_1^{2}}$，只是将 $\frac{\partial z_1^{2}}{\partial w_{11}^{2}}$换为 $\frac{\partial z_1^{2}}{\partial b_1^{2}}$。
对应一致的迭代形式： $b_1^{2}=b_1^{2}+\eta g$

这样就完成了一轮从后向前的传播，再继续向前转播以 $w_{33}^{1}$为例：
通过 $z_3^{1}=x_1w_{31}^{1}+x_2w_{32}^{1}+x_3w_{33}^{1}+b_3^{1}$
$a_3^1=sigmoid(z_3^{1})$
但是在这里的 $a_3^1$有多条路径影响后面的最终输出
$z_1^{2}=a_1^1w_{11}^{2}+a_2^1w_{12}^{2}+a_3^1w_{13}^{2}+b_1^{2}$
$\hat y_1=a_1^2=sigmoid(z_1^{2})$

$z_2^{2}=a_1^1w_{21}^{2}+a_2^1w_{22}^{2}+a_3^1w_{23}^{2}+b_2^{2}$
$\hat y_2=a_2^2=sigmoid(z_2^{2})$
再到 $H(\hat y,y)$来影响最终结果。
由于代价函数中是将 $\hat y_1,\hat y_2$对应的误差值结合（无论是求欧式距离，还是交叉熵），所以这里我们将两条路径的偏导相加有：
路径一： $w_{33}^{1}->z_3^{1}->a_3^1->z_1^{2}->\hat y_1$
$g_1=\frac{\partial \hat y_1}{\partial w_{33}^{1}}=\frac{\partial \hat y_1}{\partial z_1^{2}}\frac{\partial z_1^{2}}{\partial a_3^1}\frac{\partial a_3^1}{\partial z_3^{1}}\frac{\partial z_3^{1}}{\partial w_{33}^{1}}$
路径二： $w_{33}^{1}->z_3^{1}->a_3^1->z_2^{2}->\hat y_2$
$g_2=\frac{\partial \hat y_2}{\partial w_{33}^{1}}=\frac{\partial \hat y_2}{\partial z_2^{2}}\frac{\partial z_2^{2}}{\partial a_3^1}\frac{\partial a_3^1}{\partial z_3^{1}}\frac{\partial z_3^{1}}{\partial w_{33}^{1}}$
结合一下有：
$g=\frac{\partial H(\hat y,y)}{\partial w_{33}^{1}}=\frac{\partial H(\hat y,y)}{\partial \hat y_1}g_1+\frac{\partial H(\hat y,y)}{\partial \hat y_2}g_2$
最终的迭代形式： $w_{33}^{1}=w_{33}^{1}+\eta g$

同理对于相应的偏置值 $b_1^{1}$，只是将 $\frac{\partial z_3^{1}}{\partial w_{33}^{1}}$转变为 $\frac{\partial z_3^{1}}{\partial b_1^{1}}$即可：
路径一： $b_1^{1}->z_3^{1}->a_3^1->z_1^{2}->\hat y_1$
$g_1=\frac{\partial \hat y_1}{\partial b_1^{1}}=\frac{\partial \hat y_1}{\partial z_1^{2}}\frac{\partial z_1^{2}}{\partial a_3^1}\frac{\partial a_3^1}{\partial z_3^{1}}\frac{\partial z_3^{1}}{\partial b_1^{1}}$
路径二： $b_1^{1}->z_3^{1}->a_3^1->z_2^{2}->\hat y_2$
$g_2=\frac{\partial \hat y_2}{\partial b_1^{1}}=\frac{\partial \hat y_2}{\partial z_2^{2}}\frac{\partial z_2^{2}}{\partial a_3^1}\frac{\partial a_3^1}{\partial z_3^{1}}\frac{\partial z_3^{1}}{\partial b_1^{1}}$
结合一下有：
$g=\frac{\partial H(\hat y,y)}{\partial b_1^{1}}=\frac{\partial H(\hat y,y)}{\partial \hat y_1}g_1+\frac{\partial H(\hat y,y)}{\partial \hat y_2}g_2$
最终的迭代形式： $b_1^{1}=b_1^{1}+\eta g$
其他的参数形式也一致，对于更多层的网络，只是相应的偏导计算更加复杂而已。

衰减与爆炸

通过上面的推导我们得到了相应的偏导形式，对于多层次的网络模型，我们会得到多个偏导函数的乘积，但是在迭代过程中某些权值对应标量值会导致偏导数取值过大或过小，过小时多个偏导取值乘积趋于0会产生"衰减"，过大即多个偏导的取值过大累乘后会更大产生"爆炸"，这些因素都会导致相应数值的不稳定从而影响模型效果。

参数初始化

对于模型中参数的初始值，一般采用的是随机初始化，如果默认参数的初始值一样，对于同一层的计算而言，正向传播中使用的也是相同的激活函数，在反向传播中可能会导致偏导值相同，迭代过程中就相当于只有一组参数对应的神经单元在起作用，所以我们不能将初始参数全部相同设置。

小结

总的来说，我们完全可以将这样一个复杂的神经网络的结构转化为一个拥有许多参数的数学模型，模型中的自变量就是对应的输入，因变量就是对应的输出，我们使用不同的训练样例（输入）与对应标记（输出）就是一个处理代价函数取最小值的过程，通过对多个参数的求偏导以及迭代计算与数学中对于函数的处理是一致的。而训练完成的模型就是一个参数确定的"函数"，给定了输入便可以得到对应的输出，而机器"学习"的过程便全部体现在了这诸多的参数（权值，偏置等）中了。