NYU机器学习第一期（补充）-代价分解（excess risk decomposition）

下文只会挑一些可以起到检验自学效果的并且有趣的地方来说明，系统的学习请前往课程资源链接。  【毕竟时间有限，和妹子吃鸡更要紧 
同自学的可以相互交流
一起从“kind of understanding”
到“actual understanding”.

课程资源

• 标有对号的问题下期给答案

机器学习课程知乎问答
下文ppt截图也来自链接里NYU的课件。

三个risk

• $f^*$:全局的且是理论上的最优解

  $f^*= \arg \min \limits_{f}\mathbb{E}l(f(x),y)$

• $f_\mathcal{F}$:假设空间上的理论最优解

  $f^{\mathcal{F}}= \arg \min \limits_{f\in \mathcal{F}}\mathbb{E}l(f(x),y)$

• $\hat{f}_n$:假设空间上的估计最优解(即用平均数估计均值）

  $f^{\mathcal{F}}= \arg \min \limits_{f\in \mathcal{F}}\frac{1}{n}\sum^n_{i=1}l(f(x_i),y_i)$

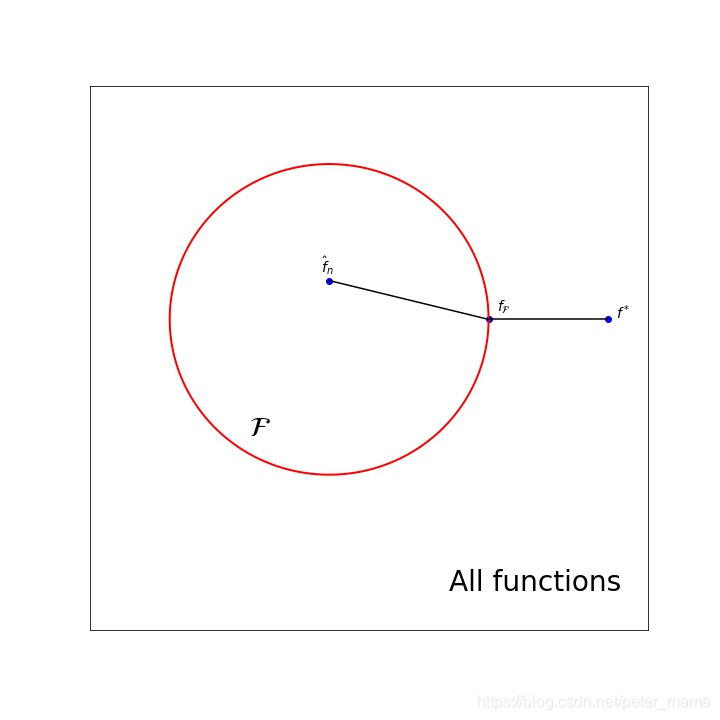
• 上图python代码

import numpy as np
import matplotlib.pyplot as plt
import mpl_toolkits.axisartist as axisartist
# 方框
fig = plt.figure(figsize=(10, 10))
ax = axisartist.Subplot(fig, 111)  
fig.add_axes(ax)
plt.xticks([])
plt.yticks([])
plt.xlim([-4, 3])
plt.ylim([-4, 3])
#圆
x = np.arange(-3, 3, step)
y = np.arange(-3, 3, step)
X, Y = np.meshgrid(x, y)
Z = (X+1)**2  +  Y**2
contour = plt.contour(X, Y, Z, [4], colors='r', linewidths=2.0)
# 标点和连线
plt.scatter(2.5,0, c="b")
plt.annotate("$f^*$", [2.6,0], fontsize = 14)
plt.plot([2.5,1],[0,0], color='k')
plt.plot([1,-1],[0,0.5], color='k')
plt.scatter(1,0, c="b")
plt.annotate("$f_\mathcal{F}$", [1.1,0.1], fontsize = 14)
plt.scatter(-1,0.5, c="b")
plt.annotate("$\hat{f}_n$", [-1.1,0.6], fontsize = 14)
plt.annotate("$\mathcal{F}$", [-2,-1.5], fontsize = 28)
plt.annotate("All functions", [0.5,-3.5], fontsize = 28)
plt.savefig("risks_decomposition".jpg")

两个error

• 近似误差（approximation error）
  这个用较小的假设空间近似代替全局造成的误差
  $R(f_{\mathcal{F}})-R(f^*))$
• 估计误差（estimated error）
  这个用样本平均值来估计整体数据均值产生的
  $R(\hat{f}_n)-R(f_{\mathcal{F}})$

从两个erro来看overfiting

上一期我们也提到overfiting。毕竟解决overfitting是机器学习亘古不变的一个主题，因此机器学习的中许多概念都可以和overfitting扯上关系，后面很多文章也会继续从不同角度来讲overfitting。

overfitting 在这里对应大的近似误差，可以看到当假设空间变小时，近似误差是倾向于变小，考虑极限情况，假设空间缩成了一个点，此时近似误差为0，这时候便必然是underfitting了。
误差分解类似力的分解，通过力的分解可以进行受力分析，从而解得物体的状态。如果你理解两种误差，也就明白从哪些方面去减少误差，下面这个问题可检验一下。

• 使用更多的数据可以减小近似误差吗？

多出来的一个error

在假设空间的优化过程中，一般找不到最优解，因此就引出来一个优化误差（optimization error）, $\widetilde{{f_n}}$是使用的优化方法返回的的解。
$R(\widetilde{{f_n}})-R(\hat{f}_n)$

推倒重来的一个疑问？？

• 所有的估计误差都是因为我们知道data generation distribution,反过来我们能不能先去用数据估计这个分布，再利用这个分布来计算risk,做优化呢？？