Floyd算法
Floyd算法又称为插点法,是一种利用动态规划的思想寻找给定的加权图中多源点之间最短路径的算法,与Dijkstra算法类似。
在计算机科学中,Floyd-Warshall算法是一种在具有正或负边缘权重(但没有负周期)的加权图中找到最短路径的算法。算法的单个执行将找到所有顶点对之间的最短路径的长度(加权)。 虽然它不返回路径本身的细节,但是可以通过对算法的简单修改来重建路径。 该算法的版本也可用于查找关系R的传递闭包,或(与Schulze投票系统相关)在加权图中所有顶点对之间的最宽路径。
核心思路
通过一个图的权值矩阵求出它的每两点间的最短路径矩阵。 [3]
从图的带权邻接矩阵A=[a(i,j)] n×n开始,递归地进行n次更新,即由矩阵D(0)=A,按一个公式,构造出矩阵D(1);又用同样地公式由D(1)构造出D(2);……;最后又用同样的公式由D(n-1)构造出矩阵D(n)。矩阵D(n)的i行j列元素便是i号顶点到j号顶点的最短路径长度,称D(n)为图的距离矩阵,同时还可引入一个后继节点矩阵path来记录两点间的最短路径。
采用松弛技术(松弛操作),对在i和j之间的所有其他点进行一次松弛。所以时间复杂度为O(n^3);
状态转移方程:map[i,j]:=min{map[i,k]+map[k,j],map[i,j]};
时间复杂度:O(n^3);
空间复杂度:O(n^2);
图解过程
1,从任意一条单边路径开始。所有两点之间的距离是边的权,如果两点之间没有边相连,则权为无穷大。
现在我们要寻找到每两点之间的最小路径,如下图所示。
首先把图转化为一个二位数组,这个二位数组就是每条边的权重。权重的大小就是他们之间的路径距离。

2.加点
第二步就是循环加点,这里我们首先加入点①。加入①后,本部相通的②与④之间就有了一条路径,长度为(1+5)= 6 < ∞,所以就要进行更新。
加入①后还影响了②与⑥的连接,他们之间又多了一条路径,这时也需要比较1 + 9 < 8,所以②与⑥的最短路径保持原来的不变,不进行更新。

继续加入节点②,由于②本身的基础连接比较多,所以影响的路径更多,这里在图中就不一一的详细标明。
①与③ = 1+1 //2
③与④ = 1+6 //7
③与⑥ = 1+8 //9
....
除了这些原来未连通的新增的路径外,不要忘记若有原路径的需要比较(当然,程序是不是忘记的,毕竟是一个for循环)。
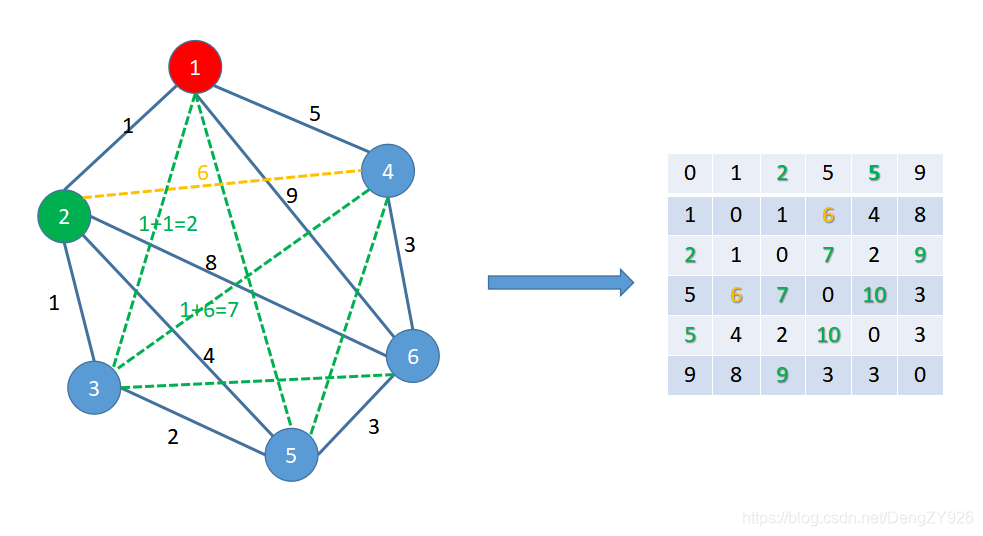
重复上面的操作,知道每个点都加入后,那么最终得到的就是一个每个点亮亮之间最短的路径了。

核心的转移方程:map[i,j]=min[map[i,k]+map[k,j],map[i,j]];
整个过程的核心代码只有4行
for (let k = 0; k < 6; k++){
for (let i = 0; i < 6; i++)// 松弛i行
{
for (let j = 0; j < 6; j++)// 松弛i列
{
map[i][j] = Math.min(map[i][j], map[i][k] + map[k][j]);
}
}
}完整代码如下:
let map = [[0,1,Infinity,5,Infinity,9], //在JavaScript中Infinity表示正无穷
[1,0,1,Infinity,4,8],
[Infinity,1,0,Infinity,2,Infinity],
[5,Infinity,Infinity,0,Infinity,3],
[Infinity,4,2,Infinity,0,3],
[9,8,Infinity,3,3,0]]
for (let k = 0; k < 6; k++){
for (let i = 0; i < 6; i++)// 松弛i行
{
for (let j = 0; j < 6; j++)// 松弛i列
{
map[i][j] = Math.min(map[i][j], map[i][k] + map[k][j]);
}
}
}
console.log(dist);其他问题
为什么时间复杂度是O(n^3)
因为每个节点都要被加入一次,每加入一个节点后,对每两两之间的路径都要进行更新,那么3层循环,每层都是n次,所以总共就是n^3。
结语
Floyd算法适用于APSP(All Pairs Shortest Paths,多源最短路径),是一种动态规划算法,稠密图效果最佳,边权可正可负。此算法简单有效,由于三重循环结构紧凑,对于稠密图,效率要高于执行|V|次Dijkstra算法,也要高于执行|V|次SPFA算法。
优点:容易理解,可以算出任意两个节点之间的最短距离,代码编写简单。
缺点:时间复杂度比较高,不适合计算大量数据。
最后欢迎访问本文个人网站:https://www.dzyong.com
