数据结构复习 ---- 最小生成树之克鲁斯卡尔（Kruskal）算法

最小生成树定义

我们把构造连通网的最小代价生成树称为最小生成树；也就是将一个带权值的连通图将各个点连通，使得所有连通的边的权值之和最小；
找连通网的最小生成树有两种经典算法，分别为普里姆算法和克鲁斯卡尔算法；这一篇总结克鲁斯卡尔算法；

Kruskal算法定义

假设N=（V,{E}）是连通网，则令最小生成树的初始状态为只有n个顶点而无边的非连通图T={V,{}},图中每个顶点自成一个连通分量。在E中选择代价最小的边，若该边依附的顶点落在T中不同的连通分量上，则将此边加入到T中，否则舍去此边而选择下一条代价最小的边。依次类推，直至T中所有顶点都在同一连通分量上为止。
此算法的Find函数由边数e决定，时间复杂度为O(loge)，而外面有一个for循环e次，所以克鲁斯卡尔算法的时间复杂度为O(eloge)；

Kruskal代码思路及实现

搞懂算法首先要清楚边集数组，然后要弄清楚Find函数的工作机制，Find函数其实就是一个防止边路形成环路的的循环，这里建议一步一步的走这个算法，把parent数组的值一步一步列出来，来看Find函数是怎么检测边集产生环路的~
struct Edge边的结构体；
TransAndSort将邻接矩阵转换成边集数组的函数；
具体细节看注释~

struct Edge {
	int begin;
	int end;
	int weight;
};

void TransAndSort(Graph &graph, Edge edges[]) {
	int index = 0;
	//遍历邻接矩阵将边放入边集数组
	for(int i = 0; i < graph.numVertexes; ++i) {
		for(int j = i + 1; j < graph.numVertexes; ++j) {
			if(graph.arc[i][j] != 7777) {
				edges[index].begin = i;
				edges[index].end = j;
				edges[index].weight = graph.arc[i][j];
				++index;
			}
		}
	}
	
	//冒泡对边集数组进行排序
	Edge temp;
	for(int i = 0; i < graph.numEdges; ++i) {
		for(int j = i + 1; j < graph.numEdges; ++j) {
			if(edges[i].weight > edges[j].weight) {
				temp = edges[i];
				edges[i] = edges[j];
				edges[j] = temp;
			}
		}
	}
	
	cout << "生成边集数组：" << endl;
	for(int i = 0; i < graph.numEdges; ++i) {
		cout << edges[i].begin << "  " << edges[i].end << "  " << edges[i].weight << endl;
	}	
}

int Find(int *parent, int i) {
	//循环追溯顶点，防止产生环路
	while(parent[i] > 0) {
		i = parent[i];
	}
	return i;
}

void MiniSpanTreeByKruskal(Graph graph) {
	Edge edges[graph.numEdges];			//定义边集数组
	int parent[graph.numVertexes];		//定义一个功能数组来判断边与边是否形成环路

	TransAndSort(graph, edges);
	
	for(int i = 0; i < graph.numVertexes; ++i) {
		parent[i] = 0;		//将parent数组初始化为0
	}
	
	int n, m;
	//循环每一条边
	for(int i = 0; i < graph.numEdges; ++i) {
		n = Find(parent, edges[i].begin);
		m = Find(parent, edges[i].end);
		//如果m和n不相等，说明此边没有与现有生成树的边形成环路
		if(n != m) {
			parent[n] = m;	//将此边的结尾顶点放入下标为起点的parent中，表示此顶点已经在生成树集合中
			cout << edges[i].begin << "--" << edges[i].end << "  ";
		}
	}
}

测试

#include<iostream>

using namespace std;

#define MAXVEX 20
#define INFINITY 7777	//用于初始化时填充邻接矩阵 

typedef struct Graph {
	char vexs[MAXVEX];
	int arc[MAXVEX][MAXVEX];
	int numVertexes, numEdges;
}*pGraph; 

struct Edge {
	int begin;
	int end;
	int weight;
};

void CreateGraph(Graph &graph) {
	cout << "输入顶点数和边数:";
	cin >>  graph.numVertexes >> graph.numEdges;
	
	//建立顶点表 
	for(int i = 0; i < graph.numVertexes; ++i) {
		cout << "请输入第" << i + 1 << "个顶点名:"; 
		cin >> graph.vexs[i];
	}
	
	//初始化邻接矩阵
	for(int i = 0; i < graph.numVertexes; ++i) {
		for(int j = 0; j < graph.numVertexes; ++j) {
			graph.arc[i][j] = INFINITY;
		}
	} 
	
	//建立邻接矩阵
	int x, y, w;
	for(int i = 0; i < graph.numEdges; ++i) {
		cout << "输入边的下标x,y和权值w:";
		cin >> x >> y >> w;
		graph.arc[x][y] = w;
		graph.arc[y][x] = w;
	}
}

void TransAndSort(Graph &graph, Edge edges[]) {
	int index = 0;
	for(int i = 0; i < graph.numVertexes; ++i) {
		for(int j = i + 1; j < graph.numVertexes; ++j) {
			if(graph.arc[i][j] != 7777) {
				edges[index].begin = i;
				edges[index].end = j;
				edges[index].weight = graph.arc[i][j];
				++index;
			}
		}
	}
	
	Edge temp;
	for(int i = 0; i < graph.numEdges; ++i) {
		for(int j = i + 1; j < graph.numEdges; ++j) {
			if(edges[i].weight > edges[j].weight) {
				temp = edges[i];
				edges[i] = edges[j];
				edges[j] = temp;
			}
		}
	}
	
	cout << "生成边集数组：" << endl;
	for(int i = 0; i < graph.numEdges; ++i) {
		cout << edges[i].begin << "  " << edges[i].end << "  " << edges[i].weight << endl;
	}	
}

int Find(int *parent, int i) {
	while(parent[i] > 0) {
		i = parent[i];
	}
	
	return i;
}

void MiniSpanTreeByKruskal(Graph graph) {
	Edge edges[graph.numEdges];
	int parent[graph.numVertexes];

	TransAndSort(graph, edges);
	
	for(int i = 0; i < graph.numVertexes; ++i) {
		parent[i] = 0;
	}
	
	int n, m;
	for(int i = 0; i < graph.numEdges; ++i) {
		n = Find(parent, edges[i].begin);
		m = Find(parent, edges[i].end);
		if(n != m) {
			parent[n] = m;
			cout << edges[i].begin << "--" << edges[i].end << "  ";
		}
	}
}

int main() {
	Graph graph;
	CreateGraph(graph);
	
	for(int i = 0; i < graph.numVertexes; ++i) {
		cout << "\t" << graph.vexs[i];
	}
	cout << "\n\n";
	for(int i = 0; i < graph.numVertexes; ++i) {
		cout << graph.vexs[i] << "\t";
		for(int j = 0; j < graph.numVertexes; ++j) {
			cout << graph.arc[i][j] << "\t";
		}
		cout << "\n\n";
	}

	MiniSpanTreeByKruskal(graph);
	
	getchar();
	return 0;
}

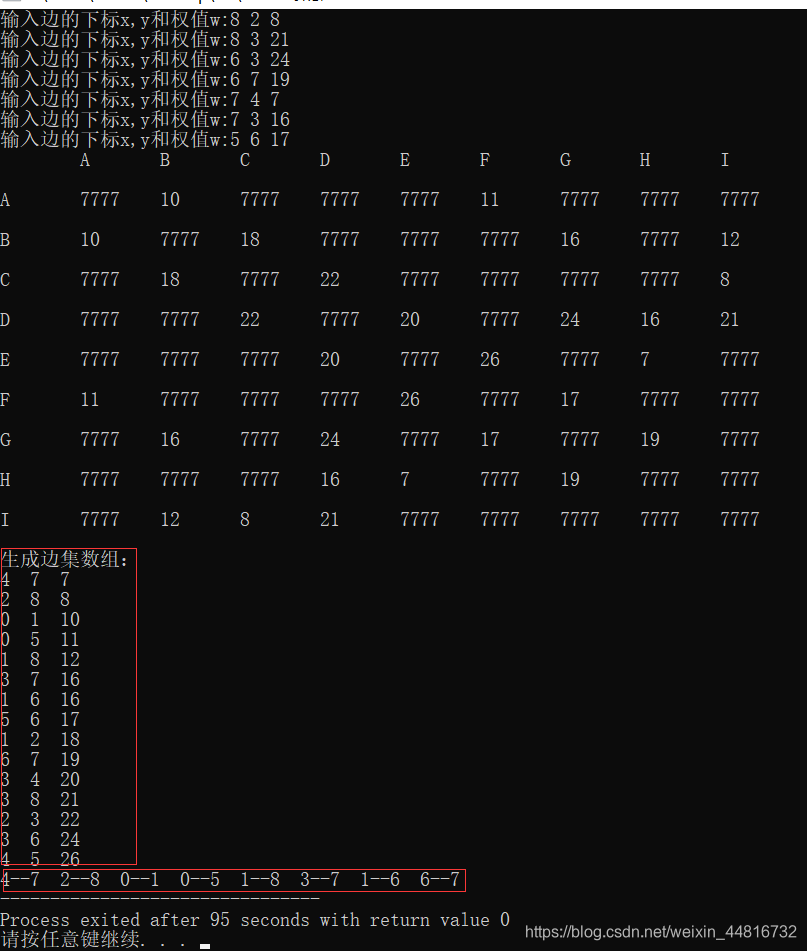
总结

克鲁斯卡尔算法的核心在于对边集数组的使用，这里邻接矩阵向边集数组的转换只是做了一个简单的遍历和冒泡排序来实现，通过Find函数对边集数组的边顶点检测是否形成环路，来判断是否能够将该边加入生成树；
对比普利姆算法，克鲁斯卡尔主要是针对边来展开，边数少时效率会非常高，所以对于稀疏图有很大优势；而普利姆算法对于稠密图，即边数非常多的情况更好一些；