定义
即轻重链剖分,通过轻重边剖分将树分为多条链,然后再通过数据结构来维护每一条链。
主要用于解决 树上 对 点权 的 区间操作 (更新/查询) 问题。
前置知识:DFS,线段树 …
相关概念
- 重儿子:对于 一个 非叶结点,其所有子结点中 子树结点数最多 的 子结点(只选一个)
- 轻儿子:对于 一个 非叶节点,其 除重结点以外 的 子结点
- 重边:连接 非叶结点 和其 重儿子 的 边
- 轻边:连接 非叶结点 和其 轻儿子 的 边
- 重链:由 相邻重边 连成的 链,重链中有且只有重边。(可以只含有一条重边)
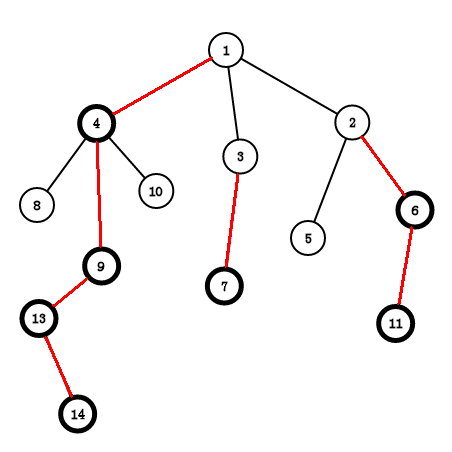
(图源自网络)例如上图, 号为重儿子, 号为轻儿子,而红边为重边,黑边为轻边。其中有 条重链: , 与 。
PS.
- 叶子结点既无重儿子,也无轻儿子;
- 不同重链之间必定被轻边相隔;
- 同一条重链上的点深度是从上到下递增的(即同一条重链不可能有两个点深度相同,因为重链是通过不断向下经过重边搜索重儿子得到的)
树链剖分过程
首先介绍需要用到的数组:
- 号结点的 点权
- 号结点的 父结点
- 号结点的 重儿子(只有一个)
- 以 号结点为根的 子树大小(即结点数量)
- 号结点的 深度
- 号结点的 新编号(以重儿子优先的DFS序)
- 号结点所在的 重链的链首(即重链上深度最小的结点)
- 新编号 为 的结点的 点权
第一次DFS(得到 和 )
int fa[maxn],dep[maxn],sz[maxn],son[maxn];
void dfs1(int u,int pre,int depth)
{
fa[u]=pre; //父结点
dep[u]=depth; //深度
sz[u]=1; //子树初始大小为 1 (仅根结点)
for(int i=head[u];i!=-1;i=e[i].next)
{
int v=e[i].v;
if(v==pre)
continue;
dfs1(v,u,depth+1); //深度+1
sz[u]+=sz[v]; //统计结点个数
if(sz[v]>sz[son[u]]) //找最大子树
son[u]=v; //最大子树根节点即为重儿子
}
}
第二次DFS(得到 和 )
int id[maxn],top[maxn],wt[maxn],tot=0;
void dfs2(int u,int TOP) //TOP表示当前u点所在重链的链首
{
top[u]=TOP;
id[u]=++tot; //新编号
wt[id[u]]=w[u]; //新编号的对应点权
if(!son[u]) //没有重儿子(一定是叶子结点,直接return;)
return;
dfs2(son[u],TOP); //※优先遍历重儿子,同一重链上,所以TOP不变
for(int i=head[u];i!=-1;i=e[i].next)
{
int v=e[i].v;
if(v!=son[u]&&v!=fa[u])
dfs2(v,v); //遍历轻儿子,链首即为本身
}
}
PS.
- 除叶结点外,所有点都有重儿子 (不论该点本身是重儿子还是轻儿子);
- 新编号 是 重儿子优先遍历的DFS序,这样可以保证 同一重链上的结点编号连续;
- 数组是为了能够通过新编号找到对应点权,实际上也可以 数组存储新编号和原编号的映射关系,达到同样目的。
实际上,以上 两点都是为了能更好地用数据结构(主要是线段树)来维护每一条链而准备的(因为同一重链上的新编号是连续的),在进行了两次DFS完成树链剖分后,接下来就是具体的应用了。
常见应用
为什么树链剖分后能解决 树上 对 点权 的 区间操作 (更新/查询) 问题?
主要基于以下两个性质:
- 对于轻边 ,
- 从根到某一点的路径上,不超过 条轻链和不超过 条重链。
利用线段树对每一条链(编号连续的区间)的操作时间复杂度为
,而路径上仅有
条链,那么可以得到总的 树上一次区间操作时间复杂度为
。
个人理解:
虽说是轻重链剖分,但是轻链(仅由轻边组成)并没有实际作用,只是与重链剖分开来而已,然后由轻边来连接各条重链,而真正要用到的是重链(因为 数组存储了每一条重链的链首),实际上我更倾向于理解成 树中全为轻边相连的重链,具体如下:
可以注意到,如果一个结点是轻儿子,且他不是叶结点,那么他一定是重链的链首( ),实际上,就算他是叶结点,也可以视为他在一条重链上,只不过该重链只有一个结点,链首也是其本身( )。
综上所诉,我们可以这样理解,所有点 都在 重链上(有可能在同一条重链,也有可能在不同重链),所有轻儿子 都是 所在重链的链首,而 所有重儿子 所在重链的链首 都是 轻儿子。
即,所有的重链都是 由轻儿子为首,剩下全为重儿子的链(重儿子数量可以为 ),然后轻边将各条重链连起来,连接重链的轻边即为 。
线段树可以维护每一条重链,而我们需要另外处理的,正是更新时找到每次需要用到的几条重链,以及查询答案时将需要的几条重链的答案合并。
①根据树上点权建立线段树(维护树上区间和为例)
线段树上每一个结点存储对应 区间(新编号)内的点权和
#define ls rt<<1
#define rs rt<<1|1
struct seg_tree
{
int sum;
int laz;
}t[maxn<<2];
void push_up(int rt)
{
t[rt].sum=t[ls].sum+t[rs].sum;
}
void build(int rt,int l,int r)
{
t[rt].laz=0; //懒标记清空
if(l==r)
{
t[rt].sum=wt[l]; //新编号对应点权
return;
}
int mid=(l+r)>>1;
build(ls,l,mid);
build(rs,mid+1,r);
push_up(rt);
}
②更新树上 号结点的值(单点更新)
void updata(int rt,int l,int r,int pos,int val) //线段树单点更新
{
...
}
updata(1,1,n,id[x],val) //传入x的新编号id[x]
③更新树上 号结点到 号结点路径上的值(区间更新)
对于 到 路径上所有的重链进行更新,步骤如下:
- 判断 和 所在重链的链首深度,优先更新链首深度更大(更深)的链;(防止“擦肩而过”)
- 更新完一条重链后移至其上面一条重链,即 链首的父结点所在链;
- 直至更新到同一条重链上,并更新当前重链后,结束。
void updata(int rt,int l,int r,int ql,int qr,int val) //线段树区间更新[ql,qr]
{
...
}
void tree_updata1(int x,int y,int val) //从x结点到y结点全部更新
{
while(top[x]!=top[y]) //不在同一重链
{
if(dep[top[x]]>=dep[top[y]]) //优先更新链首更深的
{ //重链上新编号按深度连续 ↓
updata(1,1,n,id[top[x]],id[x],val); //对应的线段树区间id[top[x]]到id[x]
x=fa[top[x]]; //转移至其上面一条重链
}
else
{
updata(1,1,n,id[top[y]],id[y],val);
y=fa[top[y]];
}
}
if(id[x]<=id[y]) //更新最后所在的同一条重链
updata(1,1,n,id[x],id[y],val);
else
updata(1,1,n,id[y],id[x],val);
}
④更新树上 号结点到根结点路径上的值(区间更新)
假设根结点为1,那么可以直接套用③的方法,令y=1即可;但由于根结点深度最小,所以可以将更新操作写得更简洁。
void updata(int rt,int l,int r,int ql,int qr,int val) //线段树区间更新[ql,qr]
{
...
}
int tree_updata2(int x,int val)
{
int res=0;
while(top[x]!=top[1]) //根结点为 1
{
updata(1,1,n,id[top[x]],id[x],val);
x=fa[top[x]];
}
updata(1,1,n,id[1],id[x],1); //根结点新编号也肯定最小
return res;
}
⑤树上更新以 号结点为根的子树(区间更新)
由于新编号是按DFS序的,所以一棵子树的编号是一定连续的;
即子树的新编号一定为 ~
void updata(int rt,int l,int r,int ql,int qr,int val) //线段树区间更新[ql,qr]
{
...
}
updata(1,1,n,id[x],id[x]+sz[x]-1,val);
⑥树上查询操作
树上查询操作和树上更新用到重链是一样的,所以将updata()替换为query()即可,对于区间和,就将query()相加;对于区间最值,就维护query()的最值;对于一些更复杂的情况,可能会需要考虑各重链之间的关系,这里不做赘述。
