NP完全性的解读与延伸

在《CLRS》（算法导论）第 33 章的 [NP 完全性] 这地方，花了很大力气才搞明白部分【题目】和【推理逻辑】。

所以，想写一份入门级的解读。

《目录》

判定问题

图灵停机问题

不可估约的复杂度

计算复杂度

可满足性问题

判定问题

大多数计算机科学家的工作是把现实问题转换为数学问题，判断这个数学问题是否可计算，如果是，就把数学问题描述成可计算问题。

“可计算”，就是不但可以算，还能算出结果来，对于计算机科学家来说：给定输入，经过计算机的有限次计算，能得到一个确定的输出就是 “可计算”。

那就从问题说起吧。

1900 年，数学大师希尔伯特列出了 23 个他认为数学中尚未解决的最重要的问题。

第十个问题是：计算一个不确定的方程（如 $x^{3}+y^{3}=z^{3}$ ），能否通过有限的步骤的运算（计算方法的有穷性），判定它是否存在整数解？

这种问题就被称为 “判定问题”。

判定问题：给定输入参数的特定值，问题就有明确的答案。

如果第十个问题能在有限的运算步骤得到解，这个问题就是【判定问题】下的一种子问题，“可判定问题” 或 “可计算问题”。

可判定问题：能够设计一个算法或计算机程序，在所有情况下都能给出正确的答案。

如果无解，那就是【判定问题】下的另一种子问题，“不可判定问题”、“不可计算问题”。

不可判定问题：无法设计一个在所有情况下都能给出正确答案的算法或计算机程序。

图灵停机问题

示例是理解的试金石。

判定方法：死循环。

如果这个问题是【可计算问题】，计算机程序一定会停下来；
如果这个问题是【不可计算问题】，计算机程序会一直计算，相当于死循环。

比如，以停机问题为例，看看判定的过程到底是咋样的~

因为死循环是判定问题的判定方法，那么，我们能不能打造一个算法用于检测另一个程序是否会出现死循环呢？

有没有这样一个程序，TA的输入是任何一段代码和这段代码的输入参数，而TA的输出则是这段代码所代表的程序，在那个参数之下运行起来之后会不会自动停机 —— 如果判断会停机，就输出“1”；如果判断不会停机、会死循环，就输出“0”。

想要做到这一点，这个判断程序必须只读、而不能去执行那段代码 —— 因为如果执行，而那段代码又真的不停机的话，计算机就会陷入死循环，这个判断程序就不能输出“0”了。

这个判断程序得能像一个高水平程序员一样，看一眼写的代码就知道其中有没有死循环。

后来，这个问题被图灵解决了，所以也叫“图灵停机问题”。

图灵的答案是：“不可能”。

在理论上就不可能存在那样的判断程序。

这是一个不可计算的问题。

为什么呢？？？

证明非常简单，反证法。

我们假设存在这么一个判断程序，称为 $Halt(p, I)$ 。

其中 $p$ 是 $Halt$ 要判断是否停机的代码， $I$ 是程序 $p$ 的输入。

也就是说，如果程序 $p$ 运行输入值 $I$ 的时候会停机，那么 $Halt(p,I) = 1$ ；否则， $Halt(p,I) = 0$ 。

好，那么我们构造下面这么一个新程序，称之为 $Z$ ：

Program (x)
If Halt(x, x) then
    永远循环
Else 停机
End

$Z$ 的输入，是任意的一段字符串 x。

$x$ 可以是一段程序的代码，也可以是一段程序的输入。

$Z$ 的规则是，如果 $Halt(x,x)$ 是 $1$ ，则 $Z$ 就永远循环下去，不停机；如果 $Halt(x,x)$ 是 $0$ ，则 $Z$ 就停机。

那么请问，像这样的一个程序 $Z$ ，如果把TA的代码自身，作为TA的输入，会怎样呢？TA会停机吗？

如果会停机，那就意味着 $Halt(Z,Z) = 1$ ，对吧？

可是您带入 $Z$ 的规则之中，这时候 $Z$ 就应该不停机。

反过来说，如果 $Z$ 不会停机，那么 $Halt(Z,Z) = 0$ ，带入规则之后 $Z$ 又会停机！悖论！

所以 $Halt$ 这样的程序，根本就不可能存在。

证明完毕。

这个悖论的关键点就在于，一段代码，既是可执行的程序，又可以作为输入的字符串。

不可估约的复杂度

那些不可计算的问题的复杂度是不可估约的，哪怕我们知道TA的计算规则，不等TA自个演化我们还是预测不了结果。

这种不可预测的复杂度是由史蒂芬·沃尔夫勒姆(Stephen Wolfram) 提出的，软件 Mathematica 、Wolfram|Alpha 就是大佬的作品。

示例是理解的试金石。

我们从一个简单的游戏说起：元胞自动机。

这张图叫“元胞自动机”，游戏非常简单。

从上往下看，您可以看到图中有很多小格子。

最上面一行只有一个黑点。此下每一行，每个格子是黑是白，由TA头顶上三个格子的颜色决定。

具体的规则一共有八条，都列在图的下面。

如，若上方三个都是黑格，那这一格子就是黑格。如果上方三个格子是【黑-黑-白】，接下来依然是黑格；如果是【黑-白-黑】，接下来是白格，以此类推。

这样按照规则一行一行地画满整个画面，就得到一个三角形的图案。

这个规则非常简单，产生图案也不复杂。

但如果对规则稍加变动，就会得到非常不一样的图形。

如果修改俩个规则如下图：

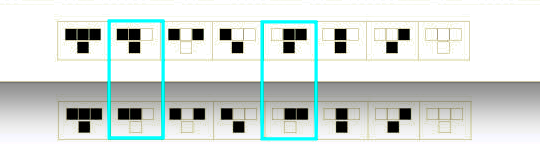
产生的图形如下：

图中的三角形有大有小，层层嵌套。但这也是简单规则所产生的简单图形，有一定结构但不复杂。

忽略【图2】，对比【图1】、【图2】的黄色部分，这里修改了俩个规则：

产生的图形如下：

依然是看似平常的八条规则，但所产生的图形就变得非常奇怪！！！

这张图看似有规律，但并不整齐，只能说有着某种不为人知的结构。

如果让这张图继续推演下去：

最左侧的结构是简单的，越往右越复杂，有很多三角形的图案，可是这些图案的出现也没有固定规律。

这张图，才是真正意义上的“复杂”。

产生这张图的这套规则，被沃尔夫勒姆命名为“ 第30号规则 ” —— 沃尔夫勒姆甚至说，这个“第30号规则”，就是他本人迄今为止最大的发现！

一套特别简单的规则，居然演化出了一个特别复杂的结果。

而且沃尔夫勒姆说，这个结果的“复杂”，跟你用任何一套复杂规则所能产生的复杂结果的“复杂”，是一样的“复杂”。

后来，沃尔夫勒姆在其著作《A New Kind of Science》中，提出了 “计算等效原理”。

这一原理说，像前面那些简单程序得到的是简单结果，但只要结果超过了一个很小的界限，所有的程序，不管有多复杂，最后得到的结果，都是同等的复杂，并不能说哪个更复杂。

再说白了，我们可以得出一个非常有意思的结论：即使是再先进的事物，TA的复杂度和我们刚刚看到的图形的复杂度，其实也是一样的。
据此，沃尔夫勒姆就得到几个非常重要、甚至能让人震惊的思想。

首先是计算不可约性（Computational Irreducible） —— 真正复杂的东西是无法进行简化的。

这就导致一个问题：没有哪个复杂系统是可预测的！

比如您要预测一个什么系统，您其实有一个潜在的假设，就是您认为您有一个比这个系统更复杂的工具。

所以面对复杂系统，我们都是把TA简化成一个简单的模型，而后用超出这个简单模型的演化速度的计算速度去实现得知这个模型的未来，并以此预测原来那个复杂系统的未来。

如预测天气，您得先把自然系统的风云运动简化，而后计算这个简化的模型。

您指望计算这个简化模型的速度比天气实际演化的速度快，您才是真正的预测。

可是如果这个系统本身是不可简化的 —— 计算不可约，您就无法预测TA，唯一的办法只能坐等系统自身演化！

比如您要问我第 30 号规则产生的那个图形的第十万行上都有什么，我就没有任何捷径可走，只能老老实实把图形画到第十万行。

沃尔夫勒姆说，一切真正的复杂系统其实都是计算不可约的，也就是不可预测的。

这就很有意思了 —— 人类历史就是计算不可约的复杂！也正因为此，我们现在活着所干的一切事情才有成就感，我们才谈得上自由意志 —— 否则如果做什么事别人早就预测好了，我们演这一遍历史还有什么意思？

这里要附带说明一下，这个“计算不可约性”和“计算等效原理”，现在有人认为，在沃尔夫勒姆之前就有别人得出过类似的结论，所以沃尔夫勒姆的主要成就是实践上的而不是计算理论上的……我对这个官司没有发言权，咱们先不去管。

图形从左到右，毫无规律，看似是不可约的，但是实际上，他是通过简单的规则，通过计算机从上往下绘制的。

这个图形之所以不可预测，是因我们没有找到这个简单的规则；不过，就是知道规则，也只能老老实实的演化过来。

计算复杂度

迄今为止，我们所研究的所有算法都是【多项式时间的算法】：对于输入规模为 $n$ 的输入，在最坏情况下的运行时间是 $O(n^{k})$ ，其中 $k$ 为某一确定常数。

那是否所有的问题都可以在【多项式的时间】里寻找到解呢？

当然不是，比如上面演示的 “图灵停机问题” 就不能在 $O(n^{k})$ 的时间内解决。

接下来的内容，就是本文的重点。如果这几个概念没看懂，后面就会比较蒙。

$P$ 问题：问题的复杂度是一个多项式，即 $O(n^{k})$ 范围内。属于【可计算问题】。

大一时面临的问题差不多都是 $P$ 问题。

$NP$ 问题：问题的复杂度越过了多项式级别，属于【不可计算问题】，迄今为止，还没人找到求解的多项式时间算法。

比如，每一步围棋的最佳走法就是 $NP$ 问题。看 AlphaGo 下围棋的棋手就会感到奇怪，一些时候一步能赢二十目的，AlphaGo 却不下。

有俩个原因：

第一个，是因为找到每一步的最佳算法很难；

第二个，是因为 AlphaGo 重视相对次序，求稳；

$NPC$ 问题：如果一个 $NP$ 问题，虽然TA找不到多项式内时间的算法，但对于一个算法可以在多项式时间证明这个方法正确与否。

计算机科学界最著名的问题： $P \neq NP$ 猜想。

人们已经证明了【所有的 $P$ 问题都是 $NP$ 问题】，但反过来【所有的 $NP$ 问题都是 $P$ 问题】吗？

如果所有的 $NP$ 问题都是 $P$ 问题， $P = NP$ 猜想；
如果 $NP$ 问题中有问题不是 $P$ 问题， $P \neq NP$ 猜想。

$P \neq NP$ 猜想，是对 $P$ 问题的集合与 $NP$ 问题的集合不一致的猜想。

简单的来说， $P \neq NP$ 猜想是【即使我们能够高效的判定问题的解，也未必能高效的找出问题的解】这样一个猜想。

按照常识，应该是这样。所以有很多计算机科学家认为这个猜想是对的，只不过还没证明而已。

可反过来一想，他们深信这个这么久了，还没证明出来，会不会是判定的方向错了呢。

说一下，证明 $P \neq NP$ 猜想的捷径。

有一部分 $NP$ 问题被称为 $NP$ 完全问题，也就是 $NPC$ 问题。

$NPC$ 问题在某种意义上可以说是 $NP$ 问题中最难的问题。

因为只要证明 $NPC$ 问题中任意一个问题为 $P$ 问题，就能证明所有的 $NP$ 问题都是 $P$ 问题，即证明了 $P = NP$ 成立。

NPC 问题是挑战 $P \neq NP$ 猜想的钥匙。

可满足性问题

那我们得先找一个 $NPC$ 问题问题出来研究，历史上，第一个被证明为 $NPC$ 问题问题的问题叫 “可满足性” 问题。

除了 “可满足性” 问题，还有：

最短与最长简单路径；
欧拉回路与哈密顿圈；
......

证明 $NPC$ 问题的具体过程，不是计算机的算法分析，而是以数学方法证明。

TA的证明过程类似于证明【基于比较的排序算法最低时间复杂度是】。

排序算法是动态的，我们要证明和分析就必须用静态的视角，借助于决策树即可，具体的证明过程记录在博客《渐近记号》的最后一节。

虽然，证明 $NPC$ 问题类似于证明【基于比较的排序算法最低时间复杂度是】，但证明 $NPC$ 问题用到的特殊技巧却不是决策树，所以证明过程不一样，但大方向是这样的。

细说一下 “可满足性” 问题。

在一个布尔公式中，可以包含这样一些成分：

取值为 1 或 0 的布尔变量；
布尔连接词，如 $\wedge ~(AND),~~\vee (OR),~~ \lnot(not)$ ；（与、或、非）
括号；

对一个布尔公式来说，若存在对其变量的某种 $0$ 和 $1$ 的赋值，使得TA的值为 $1$ ，则布尔表达式是 “可满足” 的。

若布尔公式是用 $AND$ 连接若干个 $OR$ 子句，且每个子句中恰有 $k$ 个布尔变量或其否定形式，则称为 $k-CNF$ 。

如，布尔表达式 $(x_{1}\vee \lnot x_{2})\wedge (\lnot x_{1} \vee x_{3}) \wedge (\lnot x_{2} \vee \lnot x_{3})$ 是 $2-CNF$ 。

如，布尔表达式 $(x_{1}\vee \lnot x_{2} ~\vee \lnot x_{3} )\wedge (x_{2}\vee x_{3}\vee \lnot x_{4})$ 是 $3-CNF$ 。

在《算法导论》中，证明了 $3-CNF$ 是 $NPC$ 问题，证明过程很详细。

所以，求解 $3-CNF$ ，就是求解了 $NPC$ 问题，只要证明 $NPC$ 问题中任意一个问题为 $P$ 问题，就能证明所有的 $NP$ 问题都是 $P$ 问题，即证明了 $P = NP$ 成立。

求解 $3-CNF$ 最简单的方法就是枚举法，不过时间复杂度太高了。

每个变量有 $0$ 和 $1$ 俩种状态，有 $n$ 个变量，那枚举的复杂度就是 $2^{n}$ 。

$n$ 随问题的规模而扩大，这样的 $2^{n} > n^{k}$ ，因为 $k$ 是一个确定的常数。

我们需要找到一个算法，让 $2^{n}$ 的复杂度变到 $O(n^{k})$ 的范围，也就是说这个算法的复杂度不能随问题的规模增加而大幅度增加。

如果有这么个算法，那么 $P = NP$ 成立。

有人使用了随机算法，使 $2^{n}$ 的复杂度变成了 $1.5^{n}$ ，不过只是改变了底数，没有让复杂度产生量级的缩减。

论文：

Uwe Schoning. A Probabilistic Algorithm for k-SAT and Constraint Satisfaction Problems[D]. Proceedings of the 40th Annual

IEEE Symposium on Foundations of computer Science, IEEE Computer Society, 1999: 410-414.

求解可满足性问题的随机算法流程：

// 手打，要是打错了，就算了吧
procedure Random_walk(f, n, R)
{
    r = 1

    while (r <= R){
        a = <随机选取拥有 n 个变量的分配方式>
        k = 1

        while (k <= 3n){
            if <分配方式 a 满足逻辑公式f>
                return "可以满足"
            
            c = <逻辑公式得到分配方式 a 不满足的子句>
            x = <从子句 c 中随机选取变量>
            a = <对分配方式 a 的变量 x 进行非运算得到新的分配方式>
            k += 1
        }

            r += 1    
    }

    return "大概无法满足"
}

其他关于 NP 完全性的介绍，《算法导论》很详细。

Debroon

发布了129 篇原创文章 · 获赞 324 · 访问量 4万+

私信关注