一:图的存储
1.邻接矩阵—————稠密图的存储(存边多)
2.邻接表 —————稀疏图的存储(存顶点多或者边少)
3.十字链表—————邻接表的升级版
4.邻接多重表————邻接矩阵的升级版
主要讲一下邻接矩阵和邻接表为存储结构的基本算法(STL库的vector实现)
二:图的遍历
1.DFS:Depth-First-Search
深度遍历图:
1.从一个点开始有一条边与之相连就访问相邻点,如此反复,直到找不到边。
2.然后再退回上一个点看还有没有另外的边,重复{1}操作
3.如此遍历完所有的点
邻接矩阵版:
const int MAXV = 1000;
const int INF = 1000000000;
int n,G[MAXV][MAXV];//二维数组存矩阵
bool vis[MAXV] = {false};
void dfs(int u, int depth){
//标记该点访问
vis[u] = true;
//遍历u点开始遍历
for(int v = 0; v < n; v++){
//若该点未访问过,访问它,并把它作为起点继续下一轮访问,INF表示该边不存在
if(vis[v] == false && G[u][v] != INF){
dfs(v, depth + 1);
}
}
}
void dfsTrave(){
//不仅要访问u->v,v->u也访问了
for(int u = 0; u < n; u++){
if(vis[u] == false){
dfs(u, 1);
}
}
}
邻接表版:
vector<int> adj[MAXV];
int n;
bool vis[MAXV] = {false);
void dfs(int u, int depth){
//设置为已访问;
vis[u] = true;
//把所有和u点存在边的且未访问过的点,访问
for(int i = 0; i < adj[u].size; i++){
int v = adj[u][i];
if(vis[v] == false){
dfs(v, depth + 1);
}
}
}
void dfsTrave(){
//不仅访问了u->v,同时访问了v->u
for(int u = 0; u < n; u++){
if(vis[u] == false){
dfs(u, 1);
}
}
}
2.BFS: Breadth-First-Search
广度遍历图:
1.进入一个点后设为当前点,访问,并把与之相连的所有边的顶点全部访问。
2.将所有与该点相连的顶点1~n依次全部重复(1)后,把当前点设为1
3.重复(2),直到所有点遍历。
邻接矩阵版:
int n, G[MAXV][MAXV];
bool inq[MAXV] = {false};
void bfs(int u){
//设置一块队列
queue<int> q;
//导进u点,设置已访问
q.push(u);
inq[u] = true;
while(!q.empty()){//队列非空是一直执行
int u = q.front();
q.pop();//把u拿出访问它
for(int v = 0; v < n; v++){
//把u0~un-1全部遍历一遍,和u相连的边遍历一遍
if(inq[v] == false && G[u][v] != INF){//该边存在的话,把v点打入队列
q.push(v);
inq[v] = true;
}
}
}
}
void bfsTrave(){
//广度优先这里的for循环意思变了
//这里从一行变成n*n行全遍历
for(int u = 0; u < n; u++){
if(inq[u] == false){
bfs(u);
}
}
}
邻接表版:
vector<int> adj[MAXV];
int n;
bool inq[MAXV] = {false};
void bfs(int u){
queue<int> q;
q.push(u);//导进u点,设置已访问
inq[u] = true;
while(!q.empty()){
int u = q.front();
q.pop();
for(int i = 0; i < adj[u].size(); i++){//把u0~un-1全部遍历一遍,和u相连的边遍历一遍
int v = adj[u][i];
//该边存在的话,且点未访问,把v点打入队列
if(inq[v] == false){
q.push(v);
inq(v) = true;
}
}
}
}
void bfsTrave(){
//把每个u相邻的边都遍历一遍,有向图可以,无向图容易造成重复遍历
//不过这样也是为了防止图出现不连通的情况
for(int u = 0; u < n; u++){
if(inq[u] == false){
bfs(u);
}
}
}
三:图的最短路径
1.Shortest-Path and Shortest-Distance(Dijkstra:无负权图)
作为单源最短路径算法的经典,输入一个顶点可得这个点到其他各个顶点的最短路径长度。
时间复杂度为O(n^2)
原理:
原谅我嘴笨,去画了张图来表示一下,结合代码看一下。
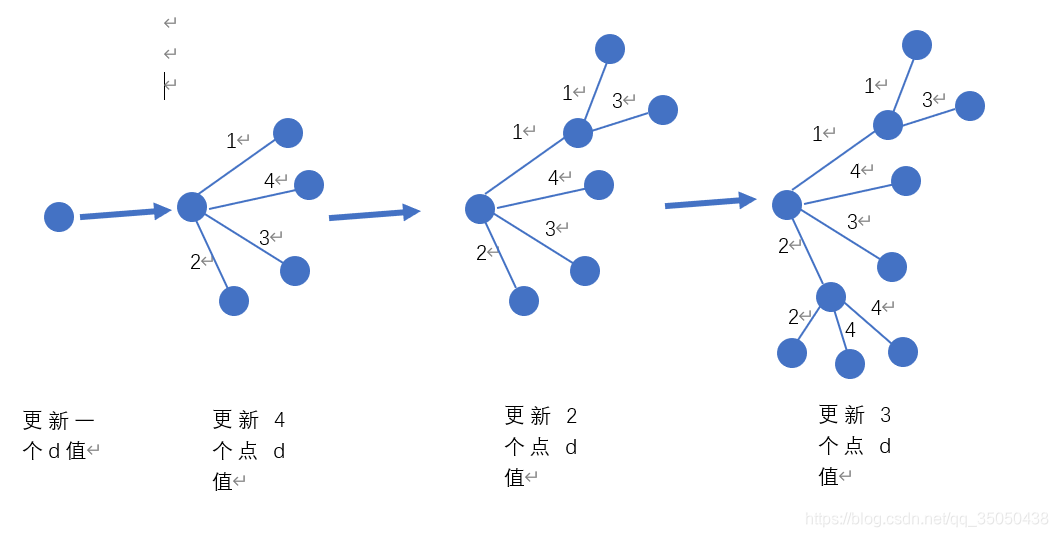
邻接矩阵版:
int n; G[MAXV][MAXV];
int d[MAXV];//d[m]存的是起点s到m点的最短距离
bool vis[MAXV] = {false};
void dijkstra(int s){
fill(d, d + MAXV, INF);//整个数组d赋值INF
d[s] = 0;//把我们的起点的距离设置为0
for(int i = 0; i < n; i++){//每次循环只能更新一次从该点相关到达其他点的最短距离,循环n就可以全部更新,并且将访问设定,不会重复更新
int u = -1; MIN = INF;//设置初值
for(int j = 0; j < n; j++){
//第一次先找到我们的起点d[s],起点到起点的距离为0,将它作为MIN最小值
//之后是找到起点相连的最短距离的点,把它作为我们下一个更新d值的点,
//再之后依旧找最小d值,所以最后会先更新出一条遍历完所有点但权值和最小的一条路
//之后就慢慢找没更新过的点,
if(vis[j] == false && d[j] < MIN){
u = j;
MIN = d[j];
}
}
//若u点初值没变,说明这个点与其他点不连通
if(u == -1) return;
//标记该点访问过
vis[u] = true;
//第一次运行是把起点所有的相连的点的距离更新了一遍
//后面要找通过d[u]的基础,把所有和u相连的点的最小d值给更新一遍
for(int v = 0; v < n; v++){
//找该点相连的点,d[u]存着起点到达该u点的最短距离权值,
//以u作为中介点,检查是否到v的距离是最小的
//邻接矩阵这里多了一个判断的原因是因为矩阵会存不连接的点设置为INF,所以要判断一下,而邻接表不会存。
if(vis[v] == false && G[u][v] != INF && d[u] + G[u][v] < d[v]){
//是的话更新
d[v] = d[u] + G[u][v];
}
}
}
}
邻接表版:
struct Node{
int v, dis;//dis存权值,v存邻接边的顶点
};
vector<Node> adj[MAXV];
int n;
int d[MAXV];
bool vis[MAXV] = {false};
void dijkstra(int s){
fill(d, d + MAXV, INF);
d[s] = 0;
//更新n个顶点,每次每个顶点会把所有相关的边的顶点d值更新一遍
for(int i = 0; i < n; i++){
int u = -1; MIN = INF;
//找未访问过且在当前d数组中权值和最小的点我们开始作为中介点
for(int j = 0; j < n; j++){
if(vis[j] == false && d[j] < MIN){
u = j;
MIN = d[j];
}
}
}
//说明剩下的点与起点不连通
if(u == -1) return;
vis[u] = true;
//更新与u点相连的顶点的最短路径d值
for(int j = 0; j < adj[u].size(); j++){
int v = adj[u][v].v;
if(vis[v] == false && d[u] + adj[u][j].dis < d[v]){
d[v] = d[u] + adj[u][j].dis;
}
}
}
2.Shortest-Path and Shortest-Distance(Floyd)
解决全源最短路径算法,不需要输入参数,直接刷出所有点他们到其他顶点的最短路径
时间复杂度是O(n^3)
而且Floyd有一个优势:代码极其简洁
原理也很简洁:
floyd是假设i点和j点间存在k点使它们相通,但是这个k点我们不知道是谁,也不知道有几个,所以我们把所有顶点全部假设一遍,然后把它们全部的距离算出来作比较取最小。这样我们设定的随机的两点最短距离我们就得到了。
所有点之间的最短距离将i和j从1到n排列组合也就全部算出来了。
可以用n*n矩阵表示并矩阵运算
#include <cstdio>
#include <algorithm>
using namespace std;
const int INF = 1000000000;
const int MAXV = 200;
int n,m;
int dis[MAXV][MAXV];//dis[i][j]表示i点到j点的最短距离
void Floyd(){
//floyd是假设i点和j点间存在k点,存在的话判断要不要更新最短距离
//而这个k点我们不知道是谁,也不知道有几个,所以我们把所有顶点全部假设一遍
for(int k = 0; k < n; k++){
//i顶点更新
for(int i = 0; i < n; i++){
//j顶点更新
for(int j = 0; j < n; j++){
//若存在且小于当前的,就更新
if(dis[i][k] != INF && dis[k][j] != INF && dis[i][k] + dis[k][j] < dis[i][j]){
dis[i][j] = dis[i][k] + dis[k][j];
}
}
}
}
}
//测试
int main(){
int u, v, w;
fill(dis[0], dis[0] + MAXV * MAXV, INF);
scanf("%d%d", &n, &m);//输入顶点数和边数
for(int i = 0; i < n; i++){
dis[i][i] = 0;//矩阵形式将所有对角点设为0
}
//我们开始创建顶点与顶点之间的边和边权值
for(int i = 0; i < m; i++){
scanf("%d%d%d", &u, &v, &w);
dis[u][v] = w;
}
Floyd();
//输出最短路径
for(int i = 0; i < n; i++){
for(int j = 0;j < n; j++){
printf("%d", dis[i][j]);
}
printf("\n");
}
return 0;
}
四: 图的最长路径(关键路径)
有向无环图:图中任意顶点都无法通过有向图回到自身
有向无环图的现实意义:
我们在现实中时间是在流逝的,无法回到过去,是不是觉着这个与有向无环图很像,没错,如果把现实生活中的事件作为点,把流逝的时间作为边,会发现生活就是一张有向无环图,发生了就再也回不去了。
事件与事件之间可以并行,但绝对不会因为你做了某件事之后可以回到原来的你曾经做的事件上。
有这么大的现实意义,那么我们就可以对其进行图的应用了。
拓扑排序(判断有向无环图)
原理:一种逻辑排序,
遵循原则:1.遍历所有点的边,判断逻辑(如果u->v,则u一定排在v前面)
2.如果u和v没有直接关系,顺序随机
3.如果出现回路,例如u->v->k->u,
u在v前面,v在k前面,k在u前面,不符合逻辑,return掉
代码的逻辑就是访问该点
通过这个原则可以判断是否是有向无环图(同时可以判定是否有环)
代码的逻辑:
1.访问一个没有入边的点,将该点所有出边全部删掉,记录+1
2.重复操作(1)、
3.检查记录是否与顶点数一致,不一致则不为有向无环图。
代码如下:
邻接表版
vector<int> G[MAXV];
int n, m, inDegree[MAXV];
bool topologicalSort(){
int num = 0;
queue<int> q;
for(int i = 0; i < n;i++){
if(inDegree[i] == 0){
q.push(i);
}
}
while(!q.empty()){
int u = q.front();
q.pop();
for(int i = 0; i < G[u].size(); i++){
int v = G[u][i];
inDegree[v]--;
if(inDegree[v] == 0){
q.push(v);
}
}
G[u].clear();
num++;
}
if(num == n) return true;
else return false;
}
关键路径:(基于有向无环图)
我们在工程的周期中,往往讨论的不是最短的路径,因为工程周期中,是多个项目并行发生,经常会出现一个项目要开始了,但是其前面的项目工作没有做好,所以导致的工期拖延。所以,我们在一开始策划工期时长时,常常要把最坏的时间考虑进去,把事件看成点,把权值看成事件可能持续时间,我们就需要求出一条最长的路径来确保这个时间是最坏的情况。
PS:之所以叫关键路径是因为: 往往这条路上的事件,如果出问题了,那么就一定会导致整个工期的拖延,而不是这条路上的事件如果出现问题造成了拖延,最后的工期不一定会拖延。
其实最长路径只要把最短路径的权值全部取负,再求最短就行了,
但是这里讨论的是有向无环图,有更简洁的更快的写法。
我这里只给出动态规划的DAG(Directed Acyclic Graph)关键路径求法:
至于代码原理,在接下来的动态规划章节进行详述:
求最大路径长度
邻接矩阵版
int DP(int i){
if(dp[i] > 0) return dp[i];
for(int j = 0; j < n; j++){
if(G[i][j] != INF){
dp[i] = max(dp[i], DP(j) + G[i][j]);
}
}
}
求最大路径的具体路径
邻接矩阵版
int DP(int i){
if(dp[i] > 0) return dp[i];
for(int j = 0; j < n; j++){
if(G[i][j] != INF){
int temp = DP(j) + G[i][j];
if(temp > dp[i]){
dp[i] = temp;
choice[i] = j;
}
}
}
return dp[i];
}
void printPath(int i){
printf("%d", i);
while(choice[i] != -1){
i = choice[i];
printf("->%d", i);
}
}
