《机器学习》第十章 降维与度量学习

10.1 k近邻学习

内容：通过被预测点周围点的标签，按照少数服从多数的原则进行预测。

优点：方法简单，同时错误率仅是贝叶斯的两倍。
缺点：1.容易受到极端点的影响；2.结果难以解释。

学习之处：

· “对任意x和任意小整数δ，在x附近δ距离范围内总能找到一个训练样本”的意思是“总能找到一个与x极度相似的解”。利用极限思想来得到一个满足一定条件的解，说明存在。
· 有目标地沿着贝叶斯分类的错误率进行推导，使用平方差公式转换以及(1+p)<=2等方法进行近似转换。

降维学习的不同之处体现在需要保留的元素的不同。

10.2 低维嵌入

内容：如何在保留重要信息的同时，提取出低维的特征。

MDS(Multiple Dimensional Scaling ，“多维缩放”):

核心思想：高低维度中的欧式距离保持不变，如何通过不变的欧式距离表示低维的特征。

推导过程如下：

实际应用:利用高维的信息计算出A,B,C和d，再推出b，最后对矩阵B做特征值分解，B=VUVᐪ，得到特征值构成的对角矩阵U，以及特征向量矩阵V，进而得到 ${Z=U\mathop{{}}\nolimits^{{1/2}}{Vᐪ}}$ (在现实中，并不一定要求欧氏距离完全相同，做到近似即可，因此有时被降低的维度可能远远小于原始维度)

很重要的注意点：事实上，能够降低到多少维，取决于B矩阵分解得到的特征值中非零的特征的个数。（在一定的情况下，甚至不能实现降维的效果，具体的实现需要对具体的给定数据进行分析）

低维嵌入总结：低维嵌入的实质就是在保持高维情况中欧式距离不变的情况下，利用不变的欧式距离得到低维情况下的结果。

10.3 线性降维

核心思想：Z=WᐪX，利用变换矩阵W，对原始高维空间进行线性变换，得到的新属性是原空间中属性的线性组合。

主成分分析（Principal Component Analysis ，简称PCA）

预备知识：坐标转换:使用基向量A,B来表示某向量R,R=xA+yB,那么x=AᐪR,y=BᐪR,

得到x,y之后，欲根据x,y进行R的重构，是需要将两者求和滴~~（x,y在A,B产生的坐标系中，均只有一个维度不为0，而R全部都不为0）

核心思想：1.最近重构性 2.最大可分性

最近重构性：将重构得到的x与原x之间的距离最小化作为目标函数。

公式推导如下
该结果对应的就是Z的所有元素之和，即Z的F范数，进而根据F范数就是矩阵的对角元素元素的迹即得到(10.15)。

ps.通过矩阵的维度来检验和计算能较快的缕清整个过程，并保证准确率。

最大可分性：投影得到的样本点之间的距离最大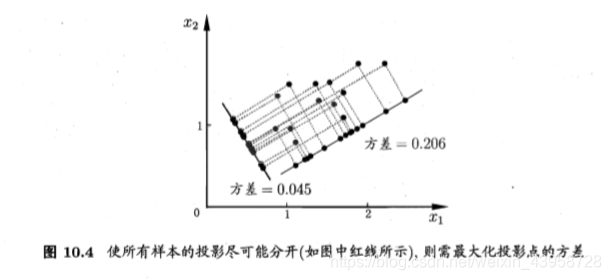

协方差矩阵:

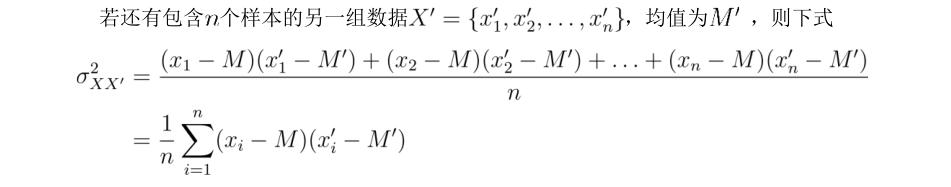
协方差矩阵的意义是说明两组数据之间的关系：
从直观上看：如果x与x’总是大于（小于）均值，那么得到的协方差就就会大于0；如果总是一个大于均值，另一个小于均值，那么得到的协方差就会小于0；如果两者与均值之间的关系一直在变化，那么协方差就会不断的正负变化。
从宏观上看：如果两者的变化趋势相同，即两者同时大于（小于）均值，那么协方差就会大于0；如果两者的变化趋势相反，即一者大于均值时，另一者小于均值，协方差就会小于0；如果两者相互独立，那么协方差就等于0，反之不然。

ps.此处的数据都是经过中心化的，中心化可以利用每个元素均减去均值的方式实现，因此只要将对应元素相乘即可。

即最终只要利用 ${\frac{{1}}{{m}}{Zᐪ}Z}$就能得到对应的协方差矩阵，可以推出 ${Max\text{  }tr \left( {Wᐪ}X{Xᐪ}W \right) }$ 实质上与最近重构等价。

使用拉格朗日乘子法，对协方差矩阵 ${X{Xᐪ} }$求进行特征值分解，并对其进行排序，取前较大的d’个特征值对应的特征向量作为主成分分析的解 ，即完成降维。

对于d’值的选择有以下两种方法:
1.通过k近邻分类器的分类准确率
2.通过最小重构的除法，将重构结果除以原结果大于某个阈值时的最小d’

主成分分析（PCA）总结：主成分分析的实质就是通过最小化降维结果与原数据的差距或者最大化降维结果的可分度来得到对应的矩阵，进而选出最大的特征值对应的特征向量作为包含最多信息的“主成分”。

10.4 核化线性降维（本处以核主成分分析为例，KPCA）

先解释一下图10.6的意思：从（b）中按照S形，得到（a），但是对于（a）,如果进行PCA，那么得到的结果是（c），而不是（b），原因就是因为由（a）到（c）默认为高维到低维的映射是线性的。

核心思想：高维基向量可以被高维的所有样本点共同表示

如果已知低维到高维的映射函数(b到a的映射函数已知)，那么就只需要在高维样本点(a)使用PCA降维就能完成低维W（基向量）的寻找；但是通常情况下，映射函数是未知的，那么我们可以使用一个特性：高维的基向量可以利用所有的样本点进行表示（10.22）。再代入PCA进行计算，就能得到（10.24），其中K是高维中的核矩阵，通过特征值分解，就能得到对应的系数α（低维基向量）【事实上，最后只需要根据K中较大特征值对应的特征向量即可】。最后，对于新的样本，可以通过（10.25）完成高维到低维的转换。
参考文章

10.5 流形学习

核心思想：高维复杂的图形中的局部信息在低维中保持不变。

10.5.1 等度量映射（Isometric Mapping ,简称Isomap）

核心思想：使用近邻距离（不变量）的不断叠加结合MDS逐步实现距离的度量。

测地线距离：沿着图形的线段距离 直线距离：两点连线距离
虽然在低维中使用两点的直线距离与测地线距离相等，然而高维中的测地线距离可能才是真正的距离，使用直线距离来度量显得不合理，因此使用近邻点距离来代替两点之间的直线距离能更好的完成距离的度量。找到所有点的k个近邻并计算出距离并把其他点距离设置为无穷大作为距离度量的方式，再使用最短路计算的方法（Dijkstra或Floyd），而后根据MDS完成得到低维的结果。对于新的样本，可以将高维的样本点作为输入，低维作为输出构造回归分类器。

10.5.2 局部线性嵌入（Locally Linear Embedding ，简称LLE）

核心思想：保持高低维中近邻变量的线性关系不变。

首先确定某个点的近邻个数，然后计算线性近似表示的近邻系数（以重构与原始的差距最小化作为目标），计算低维的样本坐标（以低维下，重构和原始的差距最小化作为目标）得到M=(I-W)ᐪ(I-W),对M进行特征值分解，选择M中最小的d’个特征值对应的特征向量。

10.6 度量学习（metric learning）

核心思想：直接对降维的距离度量方法进行最优的寻找。

找到一个距离的普遍表示方法，并对其中的参数（M）直接进行学习，并将M划入评价指标之中，完成学习。

近邻成分分析（Neighbourhood Component Analysis ,简称NCA）

类似于K近邻，不过把投票方式进行修改：根据距离远近，给出不同的概率，完成最后的判别，目标函数中存在M进行学习。