质数
在大于1的整数中,如果只包含1和本身这两个约数,就被称为质数,或者叫素数。
1.质数的判定(试除法)
时间复杂度
如果d|n,则
,则
模板
bool is_prime(int x)
{
if (x < 2) return false;
for (int i = 2; i <= x / i; i ++ )
if (x % i == 0)
return false;
return true;
}
2.分解质因数(试除法)
时间复杂度
n中最多只包含一个大于>
的质因子。
模板
void divide(int x)
{
for (int i = 2; i <= x / i; i ++ )
if (x % i == 0) //i一定是质数
{
int s = 0; //s是i的一个次数
while (x % i == 0) x /= i, s ++ ;
cout << i << ' ' << s << endl;
}
if (x > 1) //当x大于1的时候,说明x就是那个唯一大于sqrt(n)的质因子
cout << x << ' ' << 1 << endl;
cout << endl;
}
3.朴素筛法求素数
模板
int primes[N], cnt; // primes[]存储所有素数
bool st[N]; // st[x]存储x是否被筛掉
void get_primes(int n)
{
for (int i = 2; i <= n; i ++ )
{
if (st[i]) continue;
primes[cnt ++ ] = i;
for (int j = i; j <= n; j += i)
st[j] = true;
}
}
4.线性筛法求素数
模板
int primes[N], cnt; // primes[]存储所有素数
bool st[N]; // st[x]存储x是否被筛掉
void get_primes(int n)
{
for (int i = 2; i <= n; i ++ )
{
if (!st[i]) primes[cnt ++ ] = i;
for (int j = 0; primes[j] <= n / i; j ++ )
{
st[primes[j] * i] = true;
if (i % primes[j] == 0) break;
}
}
}
5.试除法求所有约数
一个数
的约数都是成对出现的,即
对应
,但有一种情况要特判
。
模板
vector<int> get_divisors(int x)
{
vector<int> res;
for (int i = 1; i <= x / i; i ++ )
if (x % i == 0)
{
res.push_back(i);
if (i != x / i) res.push_back(x / i);
}
sort(res.begin(), res.end());
return res;
}
6.约数个数和约数之和
模板
如果 N = p1^c1 * p2^c2 * ... *pk^ck
约数个数: (c1 + 1) * (c2 + 1) * ... * (ck + 1)
约数之和: (p1^0 + p1^1 + ... + p1^c1) * ... * (pk^0 + pk^1 + ... + pk^ck)
7.欧几里得算法
模板
int gcd(int a, int b)
{
return b ? gcd(b, a % b) : a;
}
8.欧拉函数
互质是公约数只有1的两个整数,叫做互质整数。 公约数只有1的两个自然数,叫做互质自然数。
:1 ~ n中与n互质的数的个数。
例
1 2 3 4 5 6
1,5和6互质
=2
1.分解质因数:
2.求欧拉函数
该式就是求1 ~ n中与
互质的数的个数。
通过容斥原理推出该式

求欧拉函数
模板
int phi(int x)
{
int res = x;
for (int i = 2; i <= x / i; i ++ )
if (x % i == 0)
{
res = res / i * (i - 1);
while (x % i == 0) x /= i;
}
if (x > 1) res = res / x * (x - 1);
return res;
}
例
#include <iostream>
#include <algorithm>
using namespace std;
int main(){
int n;
cin >> n;
while(n--){
int a;
cin >> a;
int res = a;
for(int i = 2;i <= a/i;i++){
if(a % i == 0){
res = res / i * (i - 1);
while (a % i == 0)
a /= i;
}
}
if(a > 1)
res = res / a * (a - 1);
cout << res << endl;
}
return 0;
}
筛法求欧拉函数
模板
int primes[N], cnt; // primes[]存储所有素数
int euler[N]; // 存储每个数的欧拉函数
bool st[N]; // st[x]存储x是否被筛掉
void get_eulers(int n)
{
euler[1] = 1;
for (int i = 2; i <= n; i ++ )
{
if (!st[i])
{
primes[cnt ++ ] = i;
euler[i] = i - 1;
}
for (int j = 0; primes[j] <= n / i; j ++ )
{
int t = primes[j] * i;
st[t] = true;
if (i % primes[j] == 0)
{
euler[t] = euler[i] * primes[j];
break;
}
euler[t] = euler[i] * (primes[j] - 1);
}
}
}
9.欧拉定理
若 与 互质,则 n)
10.乘法逆元
求a % p的乘法逆元
若整数b,m互质,并且b|a,则存在一个整数 ,使得 ,则称x为b的模m乘法逆元,记为 。
b 存在乘法逆元的充要条件是b与模数m互质。当模数m为质数时, 即为b的乘法逆元。
m)
m)
m)
x表示逆元
费马定理
p)
p)
综上推导,求b % p(质数)的逆元就是求 ,如果b是p的倍数则无解,其他情况有解。
#include<iostream>
using namespace std;
typedef long long ll;
ll quick_pow(ll a, ll b, ll p) {
ll ans = 1 % p;
while (b) {
if (b & 1)
ans = ans * a % p;
a = a * a % p;
b >>= 1;
}
return ans;
}
int main() {
int n;
cin >> n;
while (n--) {
int a, p;
cin >> a >> p;
if (p >= 2 && a % p != 0)
cout << quick_pow(a, p - 2, p) << endl;
else
puts("impossible");
}
return 0;
}
11.裴蜀定理
对于任意正整数 ,那么一定存在非零整数 ,使得
#include<iostream>
using namespace std;
int ex_gcd(int a, int b,int &x,int &y) {
if (b == 0) {
x = 1, y = 0;
return a;
}
int d = ex_gcd(b, a % b,y,x);
y -= a / b * x;
return d;
}
int main() {
int n;
scanf("%d", &n);
while (n--) {
int a, b,x,y;
scanf("%d%d", &a, &b);
ex_gcd(a, b, x, z
printf("%d %d\n", x, y);
}
return 0;
}
12.中国剩余定理
13.高斯消元
求解多元线性方程组
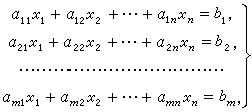
解的分布:
- 无解
- 有唯一解
- 无穷多组解

算法步骤:
- 把某一行乘一个非零的数
- 交换某两行
- 把某行的若干倍加到另一行上

- 完美阶梯形-------唯一解
- 0=非零 -------无解
- 0=0 --------无穷多组解
14.容斥原理
从n个数中选任意多个数的方案数
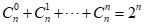
acwing890.能被整除的数

