本人做课程笔记时,很喜欢用大纲和几个简单的词语来概括,这看上去条理逻辑很清楚。因而本篇针对排队论的模型、排队状态、模型特性、到达过程、达到过程模型做了很简单的目录式梳理。
模型:
- 包(传输)->(到达)->缓冲区(排队)->处理(服务)->包(转发)
- 缓冲区:一个等待区域
- 处理(服务):一个或多个
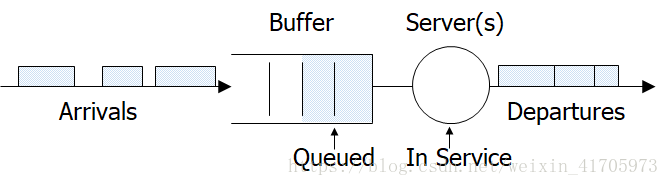
状态:
- 包(顾客)到达即到服务区-接受服务
- 包(顾客)在等待区等待-服务区已满
- 包(顾客)完成服务并离开
特性:
- 服务数量
- 缓冲区大小
- 服务方案
- 先到先服务(FCFS)
- 后到先服务(LCFS)
- 过程共享(PS Processor Sharing)等
到达过程
- 不同包(顾客)到达的时间间隔(这是一个随机变量)->随机过程
- 可以求得统计时间期望(均值)->其倒数作为到达率
- (为简化数学模型)假设是独立同分布的随机过程->
服务过程(是一个随机过程的数学模型)
- 随机过程=一系列随机变量的集合
- 每个时刻,都存在一个随机变量
- 如果时间是整数的话,此随机过程是一个离散时间随机过程;相应,如果时间是连续的,则此随机过程是一个连续时间随机过程
- 假设定义随机过程的状态空间是随机变量所有可能取值的集合
- 第n个包(顾客)在服务区的服务时间为Tsn->一个随机过程
- 求得其统计时间期望(均值),其倒数可被定义为服务速率
通用的描述:A/S/m/k
- A-到达过程
- 泊松到达的分布M(Markov ian)
- 几何到达的分布G(Geometry)
- S-服务时间分布
- M指数分布
- D确定的服务时间
- G一般分布
- m-服务的数量
- k-系统允许处理(或缓冲或被服务)的包(顾客)的最大数量(当缓冲很大~无穷时可被忽略)
- 比如:
- M/M/1:以泊松分布到达的/指数型服务时间分布的/拥有一个服务器的/无限大缓冲区的/排队模型。
- M/M/m:以泊松分布到达的/指数型服务时间分布的/拥有m个服务器的/无限大缓冲区的/排队模型。
- M/M/m/m:以泊松分布到达的/指数型服务时间分布的/拥有m个服务器的/m单位长的缓冲区的/排队模型。
- M/G/1:以泊松分布到达的/一致分布服务时间分布的/拥有一个服务器的/无限大缓冲区的/排队模型。
- n*/D/∞: 一个常数时延系统