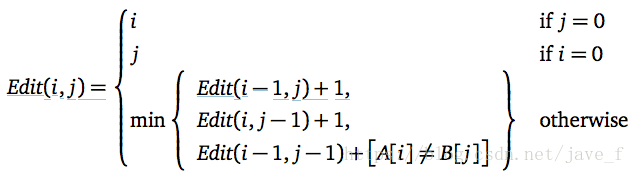动态规划 001 - 编辑距离(Levenshtein Distance)问题

问题

编辑距离(Levenshtein Distance)问题

字符串的编辑距离也被称为距Levenshtein距离（Levenshtein Distance），属于经典算法，常用方法使用递归，更好的方法是使用动态规划算法，以避免出现重叠子问题的反复计算，减少系统开销。

思考

也许我们以前遇过这样一个问题：

计算两个字符串的相似度。

关于相似度的定义，从下面这个例子了解一下：

比如，对于”abcdefg”和”abcdef”两个字符串来说，我们认为可以通过增加/减少一个”g”的方式来达到目的。把这个操作所需要的次数定义为两个字符串的距离，而相似度等于”距离+1”的倒数。也就是说，”abcdefg”和”abcdef”的距离为1，相似度为1/2=0.5。给定任意两个字符串，你是否能写出一个算法来计算它们的相似度呢？（其实这个问题的关键是要求两个字符串的编辑距离。）

这个问题其实是由俄罗斯科学家Vladimir Levenshtein在1965年提出的。

分析

*先考虑一些特殊情况：

d(null, B) = strlen(B);
d(A, null) = strlen(A);
d(A, B) = 0 当且仅当 A = B.

*再考虑一般情况下的 d(A, B)

运用动态规划求出递归方程，将原问题分解为若干个子问题进行求最优解，而后得出原问题的最优解，采用“填表的方法”。
设计步骤：对每个子问题只求解一次，将其结果保存在一张表（构造一个行数为n+1 列数为 m+1 的矩阵 , 用来保存完成某个转换需要执行的最少操作的次数, 其中，n为字符串A的长度，m为字符串B的长度)中。

对矩阵中的一点d[i][j]，保存从A[0:i]变到B[0:j]的编辑距离。其中，这里S[0:i]变到t[0:j]有三种情况，求得这三种情况的最小值作为最小操作数：

（1）设可以在k1个操作内将s[0：i-1]转换为t[0：j]，用k1+1次操作将s[0：i]转化为t[0：j]，只需要先在“s[0：i]转化为t[0：j]”的操作开端做1次移除操作移除s[i]将s[0:i]转化为s[0:i-1]，然后再做k1个操作就可以转换为t[0:j]。对应表格，对应矩阵d[i][j]处即填入k1+1。（左）

（2）设可以在k2个操作内将s[0：i]转换为t[0：j-1]，用k2+1次操作将s[0：i]转化为t[0：j]，先用k2次操作将s[0:i]转化为t[0：j-1]，然后再执行1次插入操作在“s[0:i]变成t[0：j-1]的操作”的末尾插入“增加t[j]”的一次操作，即可将s[0:i]转化为t[0:j]。对应矩阵d[i][j]处即填入k2+1。（上）

（3）设可以在k3个操作内将s[0：i-1]转化为t[0：j-1] ，此时需分情况讨论：
**若s[i]==t[j]，S[0:i]变到t[0:j]就只要k3个操作，对应矩阵d[i][j]处即填入k3;
**若s[i]！=t[j]，则需1次换操作加在s[0：i-1]转化为t[0：j-1]的操作数基础上就可以将S[0:i]变到t[0:j]，共k3+1次。对应矩阵d[i][j]处即填入k3+1。（左上角）

其实，通过上面三种情况的分析，我们可以得到下面这个递推公式：

递推公式

实现过程

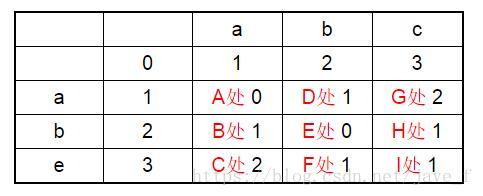
下面我们用一个简单的例子来实现下算法的过程，以abc和abe这两个字符串为例

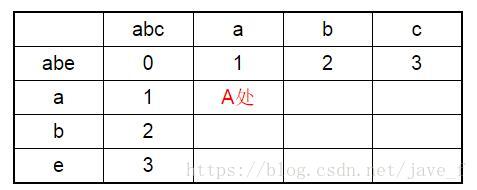
首先进行如下初始化（开辟d[n+1][m+1]数据空间，相应位置数据初始化）：

（ps:”A处”是一个标记，只是为了方便讲解，不是这个表的内容。）
计算A处的值

它的值取决于：左边的1、上边的1、左上角的0.
按照上面我们的分析：
上面的值和左面的值都要求加1，这样得到1+1=2。
A处由于是两个a相同，左上角的值加0.这样得到0+0=0。
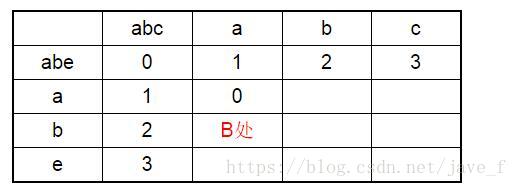
这是后有三个值，左边的计算后为2，上边的计算后为2，左上角的计算为0，所以A处取他们里面最小的0.
于是表成为下面的样子

在B处会同样得到三个值，左边计算后为3，上边计算后为1，在B处由于对应的字符为a、b，不相等，所以左上角应该在当前值的基础上加1，这样得到1+1=2，在（3,1,2）中选出最小的为B处的值。
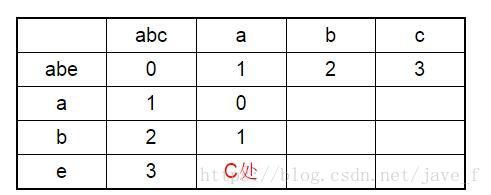
于是表就更新了

C处计算后：上面的值为2，左边的值为4，左上角的：a和e不相同，所以加1，即2+1，左上角的为3。在（2,4,3）中取最小的为C处的值。
依次推得到

I处: 表示abc 和abe 有1个需要编辑的操作。这个是需要计算出来的。
同时，也获得一些额外的信息。
A处: 表示a 和a 需要有0个操作。字符串一样
B处: 表示ab 和a 需要有1个操作。
C处: 表示abe 和a 需要有2个操作。
D处: 表示a 和ab 需要有1个操作。
E处: 表示ab 和ab 需要有0个操作。字符串一样
F处: 表示abe 和ab 需要有1个操作。
G处: 表示a 和abc 需要有2个操作。
H处: 表示ab 和abc 需要有1个操作。
I处: 表示abe 和abc 需要有1个操作。

程序实现

#include<bits/stdc++.h>
using namespace std;

int min(int a,int b,int c)
{
    return (a<b)?(a<c?a:c):(b<c?b:c);
}
int main()
{
    FILE * file;
    freopen("input.txt", "r", stdin);
    freopen("output.txt","w",stdout);

    int d[6][8];
    string a,b;
    cin>>a>>b;

    for (int i=0;i<=b.size()+1;i++)
    {
        for (int j=0; j<=a.size()+1;j++)
        {
            if (i==0&&j==0)
                d[i][j]=0;
            else if (i==0&& j > 0)
                d[i][j]=j;
            else if (i>0&&j==0)
                d[i][j]=i;

            else if(i>=1&&j>=1)
            {
                int k =((b[i-1]==a[j-1])?0:1);
                d[i][j]=min(d[i-1][j]+1, d[i][j-1]+1,d[i-1][j-1]+k);
            }
        }
    }
/*
    for(int i=0;i<b.size()+1;i++)
    {
        for(int j=0;j<a.size()+1;j++)
        {
            cout<<d[i][j]+" ";
        }
        cout<<endl;
    }
*/
    cout<<d[b.size()+1][a.size()+1];
    return 0;
}

https://my.oschina.net/mustang/blog/58125
https://blog.csdn.net/the_k1/article/details/78442814
https://www.cnblogs.com/cangT-Tlan/p/6219005.html
http://www.cnblogs.com/jiabei521/p/3353390.html
http://wdhdmx.iteye.com/blog/1343856

【附：一文一图】