动态规划 - The Levenshtein Distance 编辑距离

（一）问题样例

给你两个单词 word1 和 word2，请你计算出将 word1 转换成 word2 所使用的最少操作数。
你可以对一个单词进行如下三种操作：
• 插入一个字符
• 删除一个字符
• 替换一个字符

【示例】

输入：word1 = "benyam", word2 = "ephrem"
输出：5

（二）求解步骤

1、确定状态

-  找出最后一步
-  化成子问题
-  画出动态规划表
		-  表的最后一格表示原问题，
		-  表的任意一格表示一个子问题
- 填写动态规划表
        -  理解整个动态规划的过程

【示例】
最后一步：求benyam到ephrem的最短编辑距离
化成子问题：
分析：
1）当前问题由子问题经过Insert、delete、replace操作后得到
2）对word1 删除一个字符和对word2插入一个字符是等价的。
同理，对word2 删除一个字符和对word1插入一个字符也是等价的；
3）对word1替换一个字符和对word2替换一个字符是等价的。
这样以来，本质不同的操作实际上只有三种：
• Insert：在word2 中插入一个字符；
• Delete：在word1 中插入一个字符；
• replace：修改word1的一个字符。
画出动态规划表：

在这里插入图片描述

①表示原问题：benyam → ephrem的最短编辑距离
②表示子问题：b → ep的最短编辑距离
填写动态规划表：
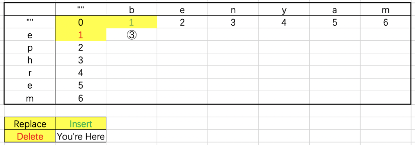
在这里插入图片描述
填写初始条件：
（1) “”、e、ep、eph、ephr、ephre、ephrem到“”的距离分别为0、1、2、3、4、5、6
（2)“”到“”、b、be、ben、beny、benya、benyam的距离分别为0、1、2、3、4、5、6
（3）对于③，当前问题“b → e的最短编辑距离”可以由其前一个子问题经过Insert、Delete或Replace而来：

选择Insert时，子问题为b → “”，子问题距离为1，b → e需要一次replace，所以当前问题距离为1+1=2
选择Delete时，子问题为“”→ e，子问题距离为1，b → e需要一次replace，所以当前问题距离为1+1=2
选择Replace时，子问题为“”→“”，子问题距离为0，b → e需要一次replace，所以当前问题距离为0+1=1

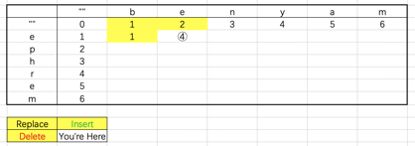
在这里插入图片描述

4）对于④，当前问题“be → e的最短编辑距离”：

选择Insert时，子问题为be → “”，子问题距离为2，be → e需一次delete操作，所以距离为2+1=3
选择Delete时，子问题为b → e，子问题距离为1，be → e需一次delete操作，所以距离为1+1=2
选择Replace时，子问题为b → “”，子问题距离为1，be → e当对于其子问题b→“”对结果没有影响，所以距离为1+0=1

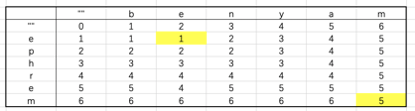
2、转移方程
• 开辟数组存储动态规划表

// DP 数组
	int n = word1.length();
    int m = word2.length();
    int [][] D = new int[n + 1][m + 1];

数组大小往往比输入大1
明确数组中每个元素的含义
e.g. D[2,1]表示be → e的最短编辑距离
根据求解DP Table的过程建立转移方程

if (word1[i] == word2[j])
	D[i][j] = D[i - 1][j - 1];
else 
	D[i][j] = min{ D[i-1][j-1], D[i-1][j], D[i][j-1] };

3、初始条件和边界情况

    // 边界状态初始化
    for (int i = 0; i < n + 1; i++) {
      D[i][0] = i;
    }
    for (int j = 0; j < m + 1; j++) {
      D[0][j] = j;
    }

4、计算顺序

    // 计算所有 DP 值
    for (int i = 1; i < n + 1; i++) 
    {
      for (int j = 1; j < m + 1; j++) 
      {
        ....
      }
    }

【示例】完整代码

public static int calStringDistance(String charA, String charB)
{
    char[] A = charA.toCharArray();
    char[] B = charB.toCharArray();
    int n = charA.length();
    int m = charB.length();

    //初始化边界状态
    int[][] DP = new int[n+1][m+1];

    //初始化边界状态
    for (int i = 0; i < A.length+1; i++) DP[i][0] = i;
    for (int j = 0; j < B.length+1; j++) DP[0][j] = j;

    //计算DP Table
    for (int i = 1; i < n + 1; i++)
        for (int j = 1; j < m + 1; j++)
        {
            if(A[i-1]==B[j-1]) DP[i][j] = DP[i-1][j-1];
            else DP[i][j] = Math.min(Math.min(DP[i-1][j],DP[i][j-1]),DP[i-1][j-1])+1;
        }

    return DP[n][m];
}

Reference:
The Levenshtein Distance