贪心、回溯、分治、动态规划,确切地讲,应该是算法思想,并不是具体的算法,常用来知道我们设计具体的算法和编码等。上一章已经详细地分析过动态规划,接下来还是结合具体问题,感受一下这些算法是怎么工作的,是如何解决问题的,再问体体会这些算法的本质。我觉得比单纯记忆原理和定义更有价值。
- 贪心算法
1. 如何理解贪心算法?
假设我们有一个可以容纳100kg物品的袋子,可以装各种物品。有以下5种豆子,每种豆子的总量和总价值各不相同。为了让袋子中所装物品的总价值最大,我们如何选择袋子装那些豆子,有该装多少呢?

这个问题很容易解决,只要先算一算每种豆子的单价,再按照单价依次从高到低来装就好了。单价从高到低排列,依次是:黑豆、绿豆、红豆、青豆、黄豆,所以,可以在袋子中装20kg黑豆、30kg绿豆、50kg红豆。这个问题解决思路显而易见,本质上借助贪心算法。
总结一下贪心算法解决问题的步骤:
首先要能联想到贪心算法:针对一组数据,定义了限制值和期望值,希望选出几个值,在满足限制值的情况下,期望值最大。类比刚刚的例子,限制值就是不超过100kg,期望值是豆子的总价值。
然后,尝试用贪心算法来解决:每次选择当前情况下,在对限制值同等贡献量的情况下,对期望值贡献最大的数据。类比刚刚的例子,在重量相同的情况下,对价值量贡献最大的豆子。
最后,举出几个例子、看贪心算法的结果是否最优。大部分情况,举几个例子验证一下就可以了。因为严格的证明贪心算法的正确性,很复杂,需要设计比较多的数学推理。另外,从实践角度来说,大部分能用贪心算法解决的问题,贪心算法的正确性都是显而易见的,不需要严格的数学证明。
然而,贪心算法的结果并不总是最优解。接下来看一个例子,在一个有权图中,从顶点的S开始,找一条到顶点T的最短路径(边的权值和最小)。贪心算法的解决思想,每次都选择一条跟当前顶点相连的权值最小的边,直到找到顶点T。求出的最短路径是S->A->E->T,路径长度是1+4+4=9。但是,贪心算法求出的结果并不是最短路径,因为路径S->B->D->T才是最短路径,路径长度是2+2+2=6。

为什么贪心算法在这种问题上不工作了呢?主要原因是,前面的选择会影响后面的选择。S->A 和S->B,接下来面对的顶点和边,是完全不同的。所以即使第一步选择最优的走法(S->A,边最短),但有可能因为这一部选择,导致后来的每一步选择都很糟糕,最终也就无缘全局最优解。
2. 实战分析贪心算法
分糖果:m个糖果和n个孩子(m<n),每个孩子最多只可以分到一个糖果,每个糖果大小不等,s1, s2, s3,..., sm。除此之外,每个孩子对糖果大小的需求也不一样,只有糖果大小 >= 孩子对糖果大小需求的时候,孩子才得到满足。这里的问题是,如何分配糖果,能尽可能满足最多数量的孩子?
可以把问题抽象成,从n个孩子中,抽取一部分孩子分配糖果,让满足的孩子的个数(期望值)达到是最大值,限制值就是糖果个数m。对于一个孩子来说,如果小的糖果可以满足,就没必要用更大糖果,这样更大的糖果可以留给对糖果需求更大的孩子。而且,满足对糖果需求大的孩子和对糖果需求小的孩子,对期望值贡献一样,那么我们就从满足需求小的孩子开始分配糖果。我们每次从剩下孩子中找出对糖果需求最小的孩子然后发给他剩下的能满足他需求的最小糖果,这样得到的分配方案,也就是满足孩子个数最多的方案。
钱币找零:假设我们1元、2元、5元、10元、20元、50元、100元这些面额的纸币,张数分别是c1、c2、c5、c10、c20、c50、c100。要支付K元,最少要用多少张纸币呢?
显而易见,我们当然是用面额最大的优先支付,如果不够,再用更小面额的纸币,剩下的用1元补齐。在贡献相同期望值(纸币张数)的情况下,我们希望多贡献点金额,这样可以让纸币数更少,这是一种贪心算法解决思路。
区间覆盖:假设有n个区间,起始点和结束端点分别是 [l1, r1], [l2, r2], [l3, r3], ..., [ln, rn] 。从它们中间选出一部分区间,满足两两不相交(端点相交的情况不算相交),问最多能选出多少个区间?

这个问题的处理思路不是很好懂,但是最好弄懂,因为这个处理思想在很多贪心算法问题中都会用到,比如任务调度,教师排课等。思路是这样的:假设 n 个区间中最左端点是 lmin,最右端点是 rmax。这个问题相当于选择几个不相交的区间,从左到右将[lmin, rmax] 覆盖上。按照起始端点从小到大的顺序对这 n 个区间排序。每次选择的时候,左端点跟前面的已经覆盖的区间不重合,右端点尽量小,这样可以让剩下的未覆盖的区间尽可能的大,就可以放置更多的区间,这实际上就是一种贪心的选择方法。

霍夫曼编码:假设我们有一个包含1000个字符的文件,每个字符占1bytes,用需要 8000bits,那有没有更加省空间的存储方式呢?为方便讨论,先假设这1000个字符只包含6个不同的字符,分别是a、b、c、d、e、f。我们知道,3个二进制位可以表示8个不同字符,所以为了尽量减少存储空间,每个字符就用3个二进制位表示,a(000)、b(001)、c(010)、d(011)、e(100)、f(101),那存储这1000个字符只需3000bits,但是还有没有更节省空间的存储方式呢?
霍夫曼编码出现了,它是一种十分有效的编码方法,广泛用于数据压缩中,压缩率一般在 20%~90%之间。霍夫曼编码不仅会考察文本中多少个字符,还考察每个字符出现的频率,根据频率的不同,选择不同长度的编码。霍夫曼编码试图用这种不等长的编码方法,来进一步增加压缩率。如何给不同频率的字符选择不同长度的编码呢?根据贪心算法,我们可以把出现频率比较多的字符用稍微短一些的编码,出现频率比较少的字符用稍微长一些的编码。
对于等长的编码来说,解压缩比较简单。比如刚才例子中,用3个bit表示一个字符。在解压缩的时候,每次从文本中读取3个二进制码,然后翻译成对应字符。但是霍夫曼编码是不等长的,这样就导致霍夫曼解压缩比较复杂。为了避免歧义,霍夫曼编码要求各个字符的编码之间,不会出现某个编码是另一个编码前缀的情况。
假设6个字符,按照出现频率从高到低依次是a、b、c、d、e、f。可以按照下表进行编码,在解压缩的时候,每次读取尽可能长的可解压的二进制串。经过这种编码压缩之后,这1000个字符只需要2100 bits 就可以了。

霍夫曼编码思想不难理解,但是如何根据出现频率,给不同的字符进行不同长度的编码,稍微需要一些技巧。把每个字符看作一个节点,并且辅带着把频率放到优先队列中。从队列中取出最小的两个节点A、B,然后新建一个节点C,频率是AB频率之和,并把C作为AB节点的父节点。再把C节点放到优先队列中。重复这个过程,直到队列中没有数据。

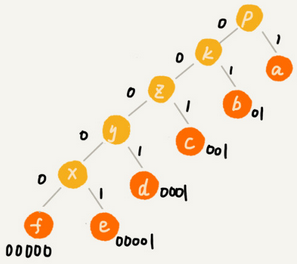
现在给每一条边加上一个权值,指向左子节点的边标记为0,指向右子节点的标记为1,那么从根节点到叶节点的额路径就是叶节点对应字符的霍夫曼编码。
贪心算法适用场景有限,一般是指导设计基础算法,如 Prim 和 Kruskal最小生成树算法、还有Dijksta 单元最短路径算法。另外,贪心算法最难的部分是如何将要解决的问题抽象成贪心算法模型,只要这一步搞定了,编码就很简单。
- 分治算法
1. 如何理解
分治算法,核心思想是分而治之,也就是将原问题划分成 n 个规模较小,并且结构越原问题类似的子问题,递归地解决这些子问题,然后在合并结果,得到原问题的解。这个定义看起来有点像递归的定义,但其实,分治是处理问题的思想,递归是一种编程技巧,分治算法一般比较适合用递归实现。分治算法的递归实现中,每一层递归都会涉及三个操作:
分解:将原问题分解成一系列子问题;
解决:递归求解每个子问题,若子问题足够小,则直接求解;
合并:将子问题的结果合并成原问题的解。
能用分治算法解决的问题,一般需要满足下面几个条件:
原问题和子问题具有相同的模式;
子问题可以独立求解,子问题之间没有相关性,这是跟动态规划最明显的区别;
具有终止分解的条件,当问题足够小的时候,可以直接求解;
可以将子问题合并成原问题,合并操作的复杂度不能太高,否则就起不到减小算法总体复杂度的效果。
2. 举例分析
如何编程求出一组数据的有序对个数或者逆序对个数?
用分治方法试试。将数组A分解为数组 A1 和 A2,分别计算 A1 和 A2的逆序对个数 K1 和 K2,然后计算 A1 与 A2之间的逆序对个数 K3,那数组A的逆序对个数就等于 K1+K2+K3。分治算法要求子问题合并的代价不能太大,那么如何快速求出 A1 与 A2之间的逆序对个数?
这里要借助归并排序算法,其中有一个关键操作,就是将两个有序的小数组,合并成一个有序的数组。在这个过程中我们就可以计算两个小数组的逆序对个数。每次合并操作,我们都计算逆序对个数,把这些逆序对个数求和就是数组的逆序对个数。

看代码:
int num = 0;
int count(int a[], int n)
{
num = 0;
mergeSortCounting(a, 0, n-1);
return num;
}
void mergeSortCounting(int a[], int p, int r)
{
if(p >= r)
return;
int q = (p+r)/2;
mergeSortCounting(a, p, q);
mergeSortCounting(a, q+1, r);
merge(a, p, q, r);
}
void merge(int a[], int p, int q, int r)
{
int i=p, j=q+1, k=0;
int *tmp = new int[r-p+1];
while(i<=q && j<=r)
{
if(a[i] <= a[j])
tmp[k++] = a[i++];
else
{
num += (q-i+1);
tmp[k++] = a[j++];
}
}
while(i<=q)
tmp[k++] = a[i++];
while(j<=r)
tmp[k++] = a[j++];
for(i=0; i<r-p; i++)
a[p+i] = tmp[i];
delete []tmp;
}3. 海量数据处理的应用
给10G的订单文件,按照金额排序,因为数据量大,如果机器内存只有几个G,就无法一次性加载到内存,也就无法单纯地使用快排、归并等基础算法来解决。要解决这个数据量大到内存装不下的问题,可以利用分治思想。可以将数据集合根据某种算法,划分成几个小的数据集合,每个小的数据集合单独加载到内存来解决,然后再将小数据集合合并成大数据集合。利用这种分治思想,还能利用多线程或者多机处理,加快处理的速度。
给10G订单排序,可以先扫描一遍订单,根据金额划分为几个金额区间,比如1~100,101~200,等等,再将它们分别放到一个小文件。这样每个小文件都可以单独加载到内存排序,最后再合并,就是最终有序的10G订单数据了。
如果订单存储在类似GFS这样的分布式系统上,当10G订单被划分成多个小文件时,每个文件可以并行加载到多台机器上处理,最后将结果合并,这样并行处理的速度也加快了很多。不过这里有一点要注意,数据的存储和计算所在的机器是同一个或者在网络中很靠近(比如在一个局域网内,数据存储速度很快),否则就会因为数据访问速度,导致整个处理过程不但不会变快反而更慢。
- 回溯算法
回溯算法有很多应用场景,深度优先搜索、正则表达式、编译原理中的语法分析、数学问题(数独、八皇后、0-1背包、图的着色、旅行商问题、全排列等)。
1. 如何理解回溯算法
人的一生有很多重要的岔路口,每个选择会影响今后的人生。有的人能做正确的选择,最后生活、事业都达到很高的高度;而有的人一路选错,最后碌碌无为。如果人生可以量化,那如何才能在岔路口做出正确的选择,让自己人生“最优”呢?
可以借助贪心算法,在每次面对岔路口的时候,都做出看起来最优的选择,期望着一组选择,是我们的人生达到“最优”。但是,贪心算法并不一定能得到最优解,可以试试回溯。电影《蝴蝶效应》,讲的就是主人公为了达到自己目标,一直通过回溯的方法,回到童年,在关键的岔路口,重新选择。这里蕴含的思想就是回溯算法。
笼统地讲,回溯算法很多时候都应用在“搜索”这类额问题上。不过这里的搜索并不是说的是狭义上的搜索,比如说图的搜索算法,而是是广义上的,在一组可能的解中,走做满足期望的解。
回溯算法思想有点类似枚举搜索,枚举所有的解,找到满足期望的解。为了有规律地枚举所有可能的解,避免重复和遗漏,我们把问题求解过程分为多个阶段。每个阶段都会面对一个“岔路口”,吸纳随意选一条路走,当发现走不通的时候(不符合期望的解),就回退到刚刚的岔路口,另选一个走法继续走。
先来看一下八皇后问题:
我们有一个8X8的棋盘,希望往里放8个棋子,每个棋子所在行、列、对角线都不能有另一个棋子。八皇后问题就是期望找到所有满足这种要求的放旗子方式。

我们把问题分为8个阶段。一次将8个棋子放第一行、第二行、第三行......第八行。在放置的过程中,我们不停的检查当前的方法,是否满足要求。如果满足,则跳到下一行继续放置棋子;如果不满足,那就再换一种方法,继续尝试。
下面是八皇后算法的代码:
int *result = new int[8]; //全局或成员变量,下标表示行,值表示列
void cal8queens(int row)
{
if(row == 8)
{
printQueens(result);
return;
}
for(int column = 0; column<8; ++column)
{
if(isok(row, column)) //有些放法不满足要求
{
result[row] = column; //第row行棋子放到column列
cal8queens(row+1); //考察下一行
}
}
}
bool isok(int row, int column)
{
int leftup = column - 1, rightup = column + 1;
for(int i=row-1; i>=0; i--) //逐行往上考察每一行
{
if(result[i] == column) //第i行column列有棋子吗
return false;
if(leftup >= 0) //考察左上对角线:第i行leftup有棋子吗
if(result[i] == leftup)
return false;
if(rightup < 8) //考察右上对角线:第i行rightup有棋子吗
if(result[i] == rightup)
return false;
leftup--;rightup--;
}
return true;
}
void printQueens(int *result)
{
for(int row=0; row<8; row++)
{
for(int column =0; column<8; column++)
{
if(result[row] == column)
cout << "Q ";
else
cout << "* ";
}
cout << endl;
}
cout << endl;
}
2. 两个回溯算法的经典应用
0-1背包问题
0-1背包是非常经典的算法问题,很多问题都可以抽象成这个问题模型。这个问题的经典解法是动态规划,但是,还有一种简单但是不那么高效的解法,就是回溯算法。0-1背包问题有很多变体,这里讲的都是比较基础的。我们有个背包,背包总的承载重量是W kg。现在我们有n 个物品,每个物品重量不等,并且不可分割,要么装要么不装,所以叫 0-1 背包问题。期望选几件物品,装到背包中。在不超过背包所能装在重量的前提下,如何使背包中的物品重量最大?
每个物品装进背包都两种装法,n 个物品,总共有2^n 种装法,去掉超过W kg的,从剩下装法中选择总重量最接近W kg的。所以,如何才能不重复地穷举出2^n种装法呢?那么就是回溯算法了,可以把物品依次排列,整个问题就分解为 n 个阶段,每个物品对应一个物品怎么选择。先对第一个物品进行处理,选择装进去或不装,然后再递归地处理剩下物品。相关diamante已经在上一章中已经讲过,这里不赘述了。
正则表达式
正则表达式中最重要的一种算法思想就是回溯。通配符的应用能表达非常丰富的语义,为了方便说明,假设正则表达式只包含 "*" 和 "?" 两种通配符,并对他们的语义稍做改变,其中,"*" 匹配任意多个(>=0)任意字符,"?" 匹配零个货一个任意字符。基于以上背景假设,下面看看如何用回溯算法,判断一个给定文本,能否跟给定的正则表达式匹配?
我们一次考察表达式的每个字符,如果是非通配符,就直接跟文本的字符匹配,如果相同则往下处理,如果不同,则回溯。
直接看代码:
bool matched = false;
int plen ;
bool match(char text[], int tlen)
{
matched = false;
rmatch(0, 0, text, tlen);
return matched;
}
void rmatch(int ti, int pj, char text[], int tlen)
{
if(matched)
return false;
if(pj == plen) //正则到达结尾
{
if(ti == tlen) //文本串也结尾了
matched = true;
return;
}
if(pattern[pj] == '*') // * 匹配任意字符
{
for(int k=0; k<tlen-ti; k++)
rmatch(ti+k, pj+1, test, tlen);
}
else if(pattern[pj] == '?') // ? 匹配0或1个字符
{
rmatch(ti, pj+1, test, tlen);
rmatch(ti+1, pj+1, test, tlen);
}
else if(ti<tlen && pattern[pj] == text[ti]) //纯字符匹配
rmatch(ti+1, pj+1, test, tlen);
}- 四种算法的比较分析
如果给它们分一下类,那贪心、回溯、动态规划可归为一类,而分治单独归为一类。因为前三个算法解决的问题模型,都可以抽象成多阶段决策最优解模型,而分治算法解决的问题大部分也是最优解问题,但是,大部分都不能抽象成多阶段决策模型。
回溯算法是个“万金油”。基本上能用跟动态规划、贪心解决的问题,都可以用回溯去解决。回溯算法相当于穷举搜索,穷举所有情况,然后得到最优解。不过回溯算法时间复杂度非常高,指数级的,只能解决小规模数据问题。对于大规模数据,执行效率就相当低。
尽管冬天规划算法高效,但并不是所有问题都可以用动态规划来解决,必须满足三个特征,最优子结构、无后效性和重复子问题。在重复子问题上,动态规划和分治算法的区分很明显,分治算法分割成的子问题,不能有重复子问题,而动态规划则相反,之所以高效,就是因为回溯算法实现中存在大量重复子问题。
贪心算法算是动态规划的一种特殊情况。解决问题更加高效,代码实现更简洁,不过他解决问题也更加有限。他能解决的问题必须满足三个条件,最优子结构,无后效性和贪心选择性。其中,最优子结构和无后效性跟动态规划无异,贪心选择性,就是通过局部最优选择,能产生全局最优选择。每一个阶段,我们都选择当前最优的决策,所有阶段的决策完之后,最终由这些局部最优解构成全局最优解。
以上所述,是本人最近在极客时间上学习数据结构和算法相关课程做的笔记吧。
