Stata: Tobit 模型

 

作者：李琼琼 (山东大学)

Stata 连享会： 知乎 | 简书 | 码云 | CSDN | StataChina公众号

Stata连享会   计量专题 || 精品课程 || 简书推文 || 公众号合集

 

连享会计量方法专题……，https://gitee.com/arlionn/Course

 

1. Tobit 模型的介绍

1.1 受限数据：截断和截堵

在做回归时，连续型的被解释变量有的时候因为截断 (Truncated) 或者截堵 (Censored) 而只能选取一定范围的值， 会导致估计量不一致。Davidson 等 (2004) 定义如果一些观测值被系统地从样本中剔除，称为 截断； 而没有观测值被剔除，但是有部分观测值被限制在某个点上则被称为 截堵。

举个例子，在研究影响家庭负债额的决定因素时，有较多的被解释变量 (负债额) 为 0，有些家庭是因为没有欠债也没有借钱给其他家庭回答负债为 0，也有家庭只借钱给其他家庭 (借钱给其他人负债额为负值)，但是后者没有在数据上反映出来。 当研究人员只选择负债大于 0 的样本，此时负债额是 截断变量； 若研究人员保留了负债大于等于 0 的样本，此时的负债额为 截堵变量。 我们将上述情形统称为 受限因变量 (limited dependent variable)，对应地就衍生出 「截断回归模型」 (truncated regression models) 和 「截堵回归模型」(censored regression models)。文献中，后者的别名还包括：「归并回归模型」和「审查回归模型」。

上述关于负债的例子属于 左侧受限，也可以将其推广到 右侧受限 (比如样本的负债额不能超过 100 万元) 或 双侧受限 (限定负债额在 0 到 100 万元之间) 的情形。

1.2 Tobit 模型设定

对于截堵数据，当左侧受限点为 0 ，无右侧受限点时，此模型就是所谓的「规范审查回归模型」，又称为 Tobit 模型 (Tobin，1958)。模型设定如下：
$\begin{aligned} y_{i}^{*} &=\mathbf{x}_{i}^{\prime} \boldsymbol{\beta}+u_i \\ u_{i} & \sim N\left(0, \sigma^{2}\right) \end{aligned}$

扫描二维码关注公众号，回复： 8565352 查看本文章

$y_{i}=\left\{\begin{array}{cl}{y_{i}^{*}} & {\text { if } y_{i}^{*}>0} \\ {0} & {\text { if } y_{i}^{ *}\leqslant0}\end{array}\right.$

当潜变量 $y^{*}$ 小于等于 0 时，被解释变量 $y$ 等于 0； 当 $y^{*}$ 大于 0 时，被解释变量 $y$ 等于 $y^{*}$ 本身，同时假设扰动项 $u_i$ 服从均值为 0 ，方差为 $\sigma^{2}$ 正态分布。

1.3 Tobit 模型的估计

由于使用 OLS 对整个样本进行线性回归，其非线性扰动项将被纳入扰动项中，导致估计不一致，Tobit 提出用 MLE 对模型进行估计。

我们先对该混合分布的概率密度函数进行推导, 再写出其对数似然函数。

当 $y_i = 0$ 时，
$\begin{aligned} \mathrm{P}(y_i=0 | \mathbf{x_i}) &=\mathrm{P}\left(y_i^{*}<0 | \mathbf{x_i}\right)=\mathrm{P}(u_{i}<-\mathbf{x_i}^{\prime} \boldsymbol{\beta} | \mathbf{x_i}) \\ &=\mathrm{P}(u_{i}/ \sigma<-\mathbf{x_i}^{\prime} \boldsymbol{\beta} / \sigma | \mathbf{x_i})=\Phi(-\mathbf{x_i}^{\prime} \boldsymbol{\beta} / \sigma)\end{aligned}$
当 $y_i > 0 $时，
$\begin{aligned} \mathrm{P}(y_i>0 | \mathbf{x_i}) &=\mathrm{P}\left(y_i^{*}>0 | \mathbf{x_i}\right)= 1 - \mathrm{P}\left(y_i^{*}\leq0 | \mathbf{x_i}\right) \\ &=1-\mathrm{P}(u_{i}\leq-\mathbf{x_i}^{\prime} \boldsymbol{\beta} | \mathbf{x_i})=1 - \mathrm{P}(u_{i} / \sigma\leq-\mathbf{x_i}^{\prime} \boldsymbol{\beta} / \sigma | \mathbf{x_i})\\ &= 1-\Phi(-\mathbf{x_i}^{\prime} \boldsymbol{\beta} / \sigma)=\Phi(\mathbf{x_i}^{\prime} \boldsymbol{\beta} / \sigma) \end{aligned}$
概率密度函数为：
$f\left(y_{i} | \mathbf{x}_{i}\right)=\left[\Phi\left(-\frac{\mathbf{x}_{i}^{\prime} \boldsymbol{\beta}}{\sigma}\right)\right]^{I_{y_{i}=0}}\left[\frac{1}{\sigma} \phi\left(\frac{y_{i}-\mathbf{x}_{i}^{\prime} \boldsymbol{\beta}}{\sigma}\right)\right]^{I_{y_{i}=0}}$ 其中 $I$ 为示性函数，当下标所表示的条件正确时取值为 1，否则为 0。

整个样本的对数似然函数为 ：

$\log L=\sum_{i=1}^{n} \left\{ I_{y_{i}=0} \ln \left[\Phi\left(-\frac{\mathbf{x}_{i}^{\prime} \boldsymbol{\beta}}{\sigma}\right)\right] +I_{y_{i}>0} \ln \left[\frac{1}{\sigma} \phi\left(\frac{y_{i}-\mathbf{x}_{i}^{\prime} \boldsymbol{\beta}}{\sigma}\right)\right] \right \}$

通过使 $\log L$ 最大化来求出 $\beta$ 和 $\sigma$。

1.4 Tobit 模型的假设检验

Tobit 模型的假设检验是通过似然比检验 (Likelihood Ratio Test, LR) 来实现的，该检验的原假设为：

$H_{0}: \boldsymbol{\beta}=\boldsymbol{\beta}_{0}$
LR 统计量为：
$L R=-2\left(\ln L_{r}-\ln L_{u}\right) \sim \chi^{2}(j)$
其中， $\ln L_{r}$ 是有约束的 ML 估计得到的似然函数值， $\ln L_{u}$ 为无约束 ML 得到的似然函数值，如果 $H_{0}$ 正确，则 $\ln L_{r}-\ln L_{u}$ 不应该为很大。

1.5 边际效应及其推导过程

在 Probit 模型和 Logit 模型等非线性模型中，估计量 $\boldsymbol{\beta}_{MLE}$ 并非边际效应 (marginal effects)，需要进行一定的转换。Tobit 模型也是一个非线性模型，估计量 $\boldsymbol{\beta}$ 无法直接作为被解释变量 $y$ (相当于截堵型被解释变量 ) 的边际效应, 但可以作为潜变量 $y^{*}$的边际效应，因为 $\boldsymbol{\beta}$ 与潜变量 $y^{*}$ 是线性关系。此外， $\boldsymbol{\beta}$ 可以表示变量 $y|y>0$ (相当于截断型被解释变量) 的期望。 下面我们从期望和偏效应入手，推导 $\boldsymbol{\beta}$ 与三种变量 $y^*、 y 和 y|y>0$ 的边际效应的关系。

 潜变量 $y^{*}$ 的期望和边际效应

• 潜变量 $y^{*}$ 关于 $\mathbf{x}$ 期望：
  $\mathrm{E}(y^{*} | \mathbf{x}) =\mathbf{x} \boldsymbol{\beta}$

• 变量 $x_j$ 对潜变量 $y^{*}$ 偏效应 (partial effects)
  $\partial \mathrm{E}(y^{*} | \mathbf{x}) / \partial x_{j}=\beta_{j}$
   截断型被解释变量 $y| y >0$ 的期望和边际效应

• 被解释变量 $y$ 关于 $y>0,\mathbf{x}$ 的期望 (又称为 “条件期望” ):
  $\begin{aligned}\mathrm{E}(y | y>0, \mathbf{x}) &=\mathbf{x} \boldsymbol{\beta}+\mathrm{E}(u | u>-\mathbf{x} \boldsymbol{\beta}) \\ &=\mathbf{x} \boldsymbol{\beta}+\sigma \mathrm{E}[(u / \sigma) |(u / \sigma)>-\mathbf{x} \boldsymbol{\beta} / \sigma ]\\ &=\mathbf{x} \boldsymbol{\beta}+\sigma \phi(\mathbf{x} \boldsymbol{\beta} / \sigma) / \Phi(\mathbf{x} \boldsymbol{\beta} / \sigma) \\ &=\mathbf{x} \boldsymbol{\beta}+\sigma \lambda(\mathbf{x} \boldsymbol{\beta} / \sigma) \end{aligned}$
  其中 $\lambda(c) =\phi(c) / \Phi(c)$ 被称为 逆米尔斯比率 (inverse Mills ratio), 是标准正态 pdf 和标准正态 cdf 在 $c$ 处之比。

• 变量 $x_j$ 对变量 $y$ 在 $y>0,\mathbf{x}$ 条件下的偏效应 (partial effects)：
  $\begin{aligned}\partial \mathrm{E}(y | y>0, \mathbf{x}) / \partial x_{j} &=\beta_{j}+ \sigma \cdot \frac{d \lambda}{d c} \frac{d c}{d x_{j}} = \beta_{j}+ \beta_{j} \cdot \frac{d \lambda}{d c} \\ &= \beta_{j}\{1-\lambda(\mathbf{x} \boldsymbol{\beta} / \sigma)[\mathbf{x} \boldsymbol{\beta} / \sigma+\lambda(\mathbf{x} \boldsymbol{\beta} / \sigma)]\} \end{aligned}$
  上式说明 $x_j$ 对变量 $y$ 在 $y>0,\mathbf{x}$ 条件下的偏效应不仅取决于 $\beta_j$，而且受到 $\{\cdot\}$ 项的影响。

 截堵型被解释变量 $y$ 的期望和边际效应

• 被解释变量 $y$ 关于 $\mathbf{x}$ 的期望 (又称为 “无条件期望” ):
  $\mathrm{E}(y | \mathbf{x})=\mathrm{P}(y>0 | \mathbf{x}) \cdot \mathrm{E}(y | y>0, \mathbf{x})=\Phi(\mathbf{x} \boldsymbol{\beta} / \sigma) \cdot \mathrm{E}(y | y>0, \mathbf{x})$

• 变量 $x_j$ 对 $y$ 在 $\mathbf{x}$ 条件下的偏效应 (partial effects)：
  $\frac{\partial \mathrm{E}(y | \mathbf{x})}{\partial x_{j}}=\frac{\partial \mathrm{P}(y>0 | \mathbf{x})}{\partial x_{j}} \cdot \mathrm{E}(y | y>0, \mathbf{x})+\mathrm{P}(y>0 | \mathbf{x}) \cdot \frac{\partial \mathrm{E}(y | y>0, \mathbf{x})}{\partial x_{j}}$
  经过化简后可得：
  $\frac{\partial \mathrm{E}(y | \mathbf{x})}{\partial x_{j}}=\beta_{j} \Phi(\mathbf{x} \boldsymbol{\beta} / \sigma)$

对以上三种边际效应进行总结：

解释变量的偏效应	函数形式
对潜变量 $y^{*}$ 的偏效应	$\partial \mathrm{E}(y^{*} | \mathbf{x}) / \partial x_{j} = \beta_{j} $
对变量 $y$ (左截断 0) 偏效应	$\partial \mathrm{E}(y | y>0, \mathbf{x})/ \partial x_{j} = \beta_{j}{1-\lambda©[c+\lambda©]} $
对变量 $y$ (左截断 0) 偏效应	$\partial \mathrm{E}(y | \mathbf{x})/ \partial x_{j} = \beta_{j}\Phi© $

注： $c = \mathbf{x} \boldsymbol{\beta} / \sigma$

 

连享会计量方法专题……

2. Stata 范例

2.1 模型估计的实现

Stata 提供 tobit 命令对归并回归模型进行估计。 在命令窗口中输入 help tobit 命令即可查看其完整帮助文件。tobit 命令的基本语法为：

 tobit depvar [indepvars] [if] [in] [weight]，11[(#)] ul[(#)] [options]

其中 ll[(#)] 表示左归并，# 是左侧受限点的具体值 ；ul[(#)] 表示右归并，# 是右侧受限点的具体值。在实际运用中，可以只选择左归并或者右归并，也可以同时选择。

下面以研究影响 非住院医疗费用 的因素为例，我们来对如何使用 Stata 做 Tobit 模型估计进行详细的介绍。

非住院医疗费用 (ambulatory expenditure，ambexp) 作为被解释变量，解释变量包括：年龄 (age), 是否为女性 (female), 教育年限 (educ) 以及 totchr, totchr 和 ins 等变量。

首先对被解释变量进行观察，

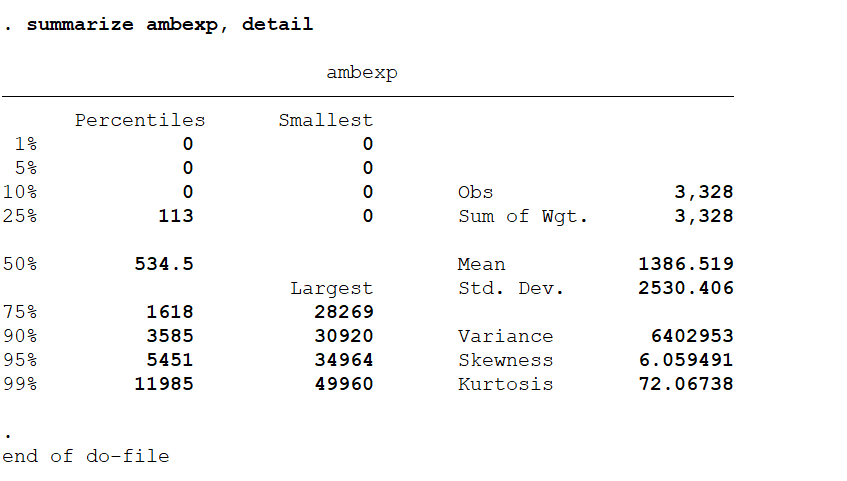
从上图可以发现，有超过 10% 的比例的被解释变量其数值为0， 这个时候我们考虑进行线性 Tobit 模型 (linear tobit model) 估计。具体的命令和估计结果如下

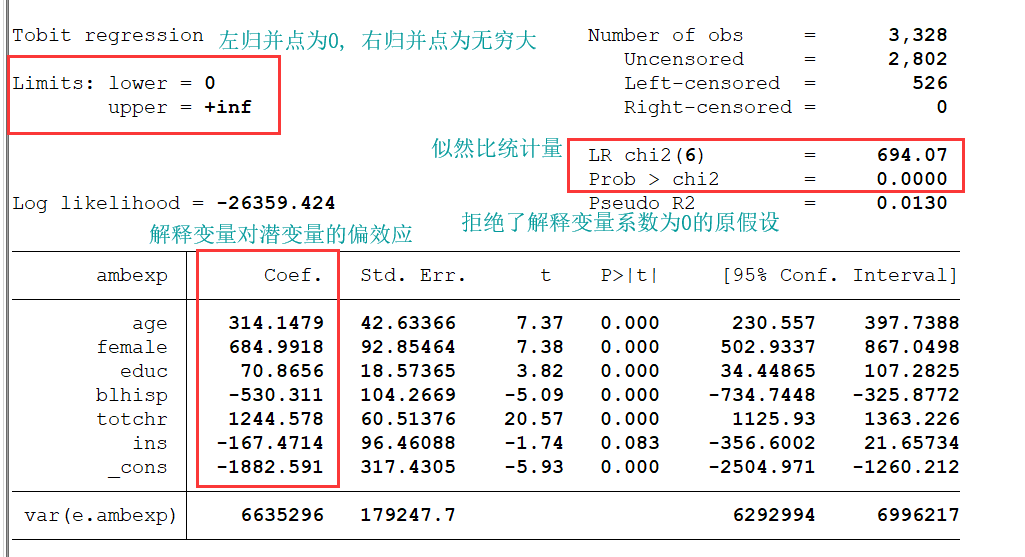
use mus16data.dta, clear
global xlist age female educ blhisp totchr ins // 定义将所有的解释变量定义为全局变量 $xlist
tobit ambexp $xlist, ll(0)

2.2 偏效应估计

在做完回归之后，使用 margins 命令分别进行三种偏边际效应的估计

• 对潜变量 $y^{*}$ 的偏效应

margins, dydx(*)

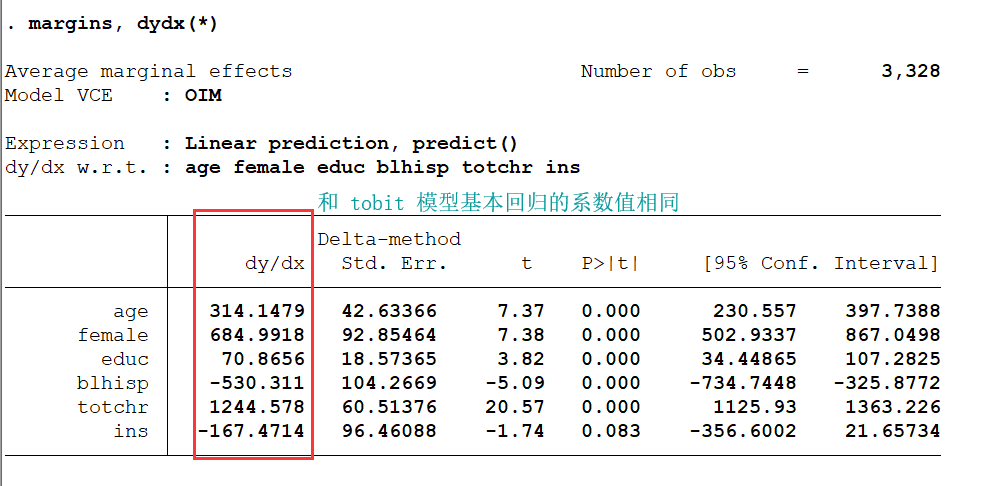
解释：以教育的为例，教育年限对在非住院医疗上的 预期花费 平均边际效应为 70.87。

• 对 $ y | y>0 $ 偏效应

margins, dydx(*) predict(e(0,.))

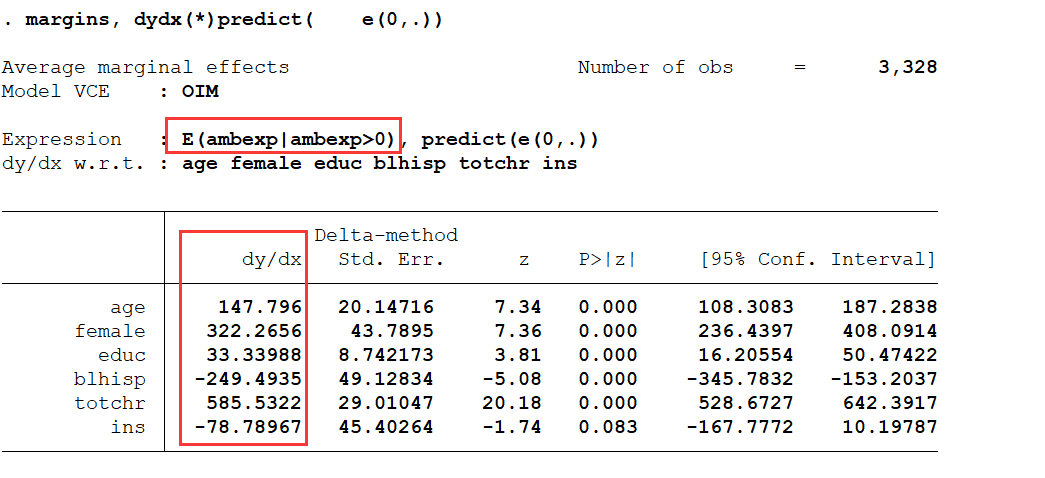
解释：相当于截断模型的平均边际效应，在非住院医疗费用的实际支出大于 0 的样本中，教育年限对于非住院医疗费用的实际支出的平均边际效应为 33.34。

• 对 $ y $ 的偏效应

margins, dydx(*) predict(  e(0,.))

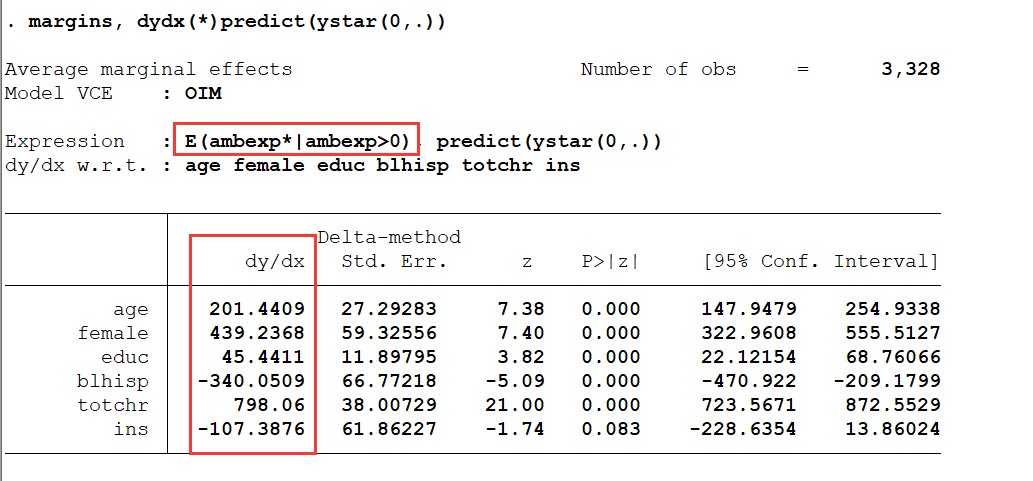
解释：教育年限对于非住院医疗费用的实际支出的平均边际效应为 45.44。

 

连享会计量方法专题……，https://gitee.com/arlionn/Course

3. 结论

在做实证研究时，虽然拥有全部的观测数据， 但是部分观测数据的被解释变量 $y$ 都被压缩在 0 这一个点上。此时，无论是整个样本还是去掉 $y$ 为 0 的样本，都无法通过 OLS 得到一致估计。因此需要使用 Tobit 模型来解决数据的截堵问题。此外，在对模型估计完以后，如果求核心变量对解释变量的偏效应，还需要经过一定的转化。

参考文献

1. Davidson R, MacKinnon J G. Econometric theory and methods[M]. New York: Oxford University Press, 2004. [PDF]
2. Wooldridge J M. Econometric analysis of cross section and panel data[M]. MIT press, 2010. [PDF]
3. Wooldridge J M. Introductory econometrics: A modern approach[M]. Nelson Education, 2016. [PDF]
4. Cameron A C, Trivedi P K. Microeconometrics Using Stata[J]. Stata Press books, 2010. [PDF]

 

关于我们

• Stata连享会 由中山大学连玉君老师团队创办，定期分享实证分析经验。
• 欢迎赐稿： 欢迎赐稿至[email protected]。录用稿件达 三篇 以上，即可 免费 获得一期 Stata 现场培训资格。
• 往期精彩推文：
  Stata绘图 | 时间序列+面板数据 | Stata资源 | 数据处理+程序 | 回归分析-交乘项-内生性

---