分治算法、贪心算法、动态规划区别与经典用例

分治思想

分治策略中，我们一般递归地求解一个问题，分为三大步骤：

• 分解：将问题划分为一些子问题，子问题的形式与原问题相同，只是规模更小
• 解决：递归求解子问题，如果子问题规模足够小，则停止递归，直接求解
• 合并：将子问题的解组合成原问题的解

分治算法的递归式：
T(n) = aT(n/b) + f(n)
其中n/b表示分治后子问题的规模，而a表示分治后子问题的数目。f(n)表示分解合并子问题花费的时间

典型用例：最大子数组问题

问题描述：
假定你获得了投资挥发性化学公司的机会，这家公司的股票价格是不稳定的，你被准许在某个时刻买进一些该公司的股票，并在一段时间后卖出，买卖都是在当天交易结束后进行。为了补偿这一机制，你可以了解股票将来的价格。你的目标是获得最大收益，毫无疑问最好的办法就是：低价买进，高价卖出。遗憾的是，在一段给定的时间内，可能无法做到在最低价格时买入股票同时在最高价格时卖出。

解法一：暴力求解
简单的尝试每对可能的买进与卖出日期，只要保证卖出日期在买进日期之前即可，假设有n天，那么可能情况可大致估计为n^2，那么此方法的时间复杂度为：

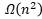
解法二：分治法
换种思路，我们定义一个新的数组A，数组A中的第i项表示第i天减去i-1天的的价格差，我们的问题就变为求数组A中和最大的非空连续子数组，分治法如何求解这个问题？问题的解可以分为三种情况

• 完全位于子数组A[low…mid]中，因此low<=i<=j<=mid
• 完全位于子数组A[mid+1…high]中，因此mid<i<=j<=high
• 跨越了中点，因此low<=i<=mid<j<=high

分解问题：

FIND-MAXIMUM-SUBARRAY(A,low,high)
if high == low
	return (low,high,A[low])
else mid = (low+high)/2
	(left_low,left_high,left_sum) =
		FIND-MAXIMUM-SUBARRAY(A,low,mid)
	(right_low,right_high,right_sum) = 
		FIND-MAXIMUM-SUBARRAY(A,mid+1,high)
	(cross_low,cross_high,cross_sum) = 
		FIND-MAXIMUM-CROSSING-SUBARRAY(A,low,mid,high)
	if left_sum >= right_sum and left_sum>=cross_sum
		return (left_low,left_high,left_sum)
	else if right_sum>= left_sum and right_sum>=cross_sum
		return (right_sum,right_high,right_sum)
	else return (cross_low,cross_high,cross_sum)

重要函数，跨越中点时的解决方法

FIND-MAXIMUM-CROSSING-SUBARRAY(A,low,mid,high)
left_sum = - ∞
sum = 0
for i = mid down to low
	sum = sum+ A[i]
	if sum >  left_sum
		left_sum = sum
		max_left = i
right_sum =  - ∞
sum = 0
for i = mid +1 to high
	sum  = sum + A[i]
	if sum > right_sum
		right_sum = sum
		max_right = i
return (max_left,max_right,left_sum+right_sum)

时间复杂度被转化为了O(n)

贪婪算法

• 将最优化问题转化为这样的形式：做出一次选择后，只剩下一个子问题需要求解
• 证明做出贪心选择后，原问题总是存在最优解，贪心选择总是安全的
• 证明做出贪心选择后，剩余的子问题满足性质，其最优解与贪心选择组合即为原问题最优解

经典用例，活动选择问题

假定有一个n个活动的集合S={a1, a2, a3, …, a4}，这些活动使用同一个资源（例如东十二302教室），每个活动ai都有一个开始时间si和一个结束时间fi，我们的教务部希望选出一个最大兼容活动集，假定每个活动已经按结束时间的单调递增顺序排列。

GREEDY-ACTIVITY-SELECTOR(s,f)
n = s.length
A={a1}
k = 1
for m = 2 to n
	if s[m] > f[k]
		A = A ∪ {am}
return A

s是所有活动开始时间的数组，f是所有活动结束时间的数组，该问题是贪婪算法的典型，每次选择兼容的最先完成的活动，该活动一定在最优解中。
证明：
A_ij为S_ij的一个最优解，a_m为A_ij中的第一个活动，设a_k为最先完成的一个活动，用a_k替换a_m得到新的解集A_ij¹

1. if a_m=a_k，则证明成立
2. else a_k.f <= a_m.f，A_ij¹中的活动不矛盾，其活动数与最优解A_ij的活动数相同，则A_ij¹同为最优解，所以a_k一定在最优解中

示例二：哈夫曼编码

HUFFMAN(C)
n = |C|
Q = C
for i = 1 to n-1
	allocate a new node z
	z.left = x = EXTRACT-MIN(Q)
	z.right = y = EXTRACT-MIN(Q)
	z.freq = x.freq + y.freq
	INSERT(Q,z)
return EXTRACT-MIN(Q)

这是贪婪算法的另一个典型问题，用于寻找最优编码方式，提高数据传输的效率。

动态规划

通常设计一个动态规划算法分四步：

1. 刻画一个最优解的结构特征
2. 递归的定义最优解的值
3. 计算最优解的值，通常采用自底向上的办法
4. 利用计算出的信息构造一个最优解

经典用例

Serling 公司购买长钢条，将其切割为锻钢条出售，切割工序本身没有成本支出，公司管理层想知道最佳的切割方案。下图为长度为 i 的钢材以及其价格p_i

长度为n的钢材，有2^n-1种切割方案（不考虑左右对称切割导致最终结果相同的问题），我们假设最优解将钢条切割为k段，最有方案为：
n = i1 + i2 + i3 +…+ ik
最大收益：
r_n = p_i1+p_i2+p_i3+…+p_ik（最优解的结构特征）
方案：
r_n = max_1<=i<=n(p_i + r_n-i)（递归定义最优解的值）

自顶向下递归实现：

CUT-ROD(p, n)
 if n==0
 	return 0
 q = -∞
 for i = 1 to n
 	q = max(q,p[i]+CUT-ROD(p, n-1))
 return q

区别与联系

分治算法一般用来解决一个规模较大不好解决的问题，将其分为多个小任务，通过解决小任务再将其合并解决大任务的一种方式，有种分而治之的感觉。

比如说给一个长度有100万的数组叫你排序，先将其分为左右各50万，先把这50万的排了，再把他们通过比较合并就可以解决问题，但是50万也不少啊，再分，分到最后给2个数排序，在合并合并合并…，你可能回想，这么分太麻烦了，但实际上你通过主方法递推就会发现，效率大大的提高了！证明如下。

贪心算法一般用来寻求最优解，一步一步的进行决策，每走一步就将解决发案的范围缩小，直到最后一步得出最优解。
比如说一张数学试卷，你在水平有限的情况下如何获得最高分? 咱们学算法的就可以用贪心法求解，第一步先把最简单的题目分数拿到，选择题前10题，填空题前两题，大题前两题，冷静保证都做对，我们可以拿80-90分，第二步，我们尝试解决选择题的第11题（总共12题），填空题的第三第四题（总共5题），大题的第三题（总共5题），尽量拿分，这样我们大概可以拿到100-110分，最后一步：我们玄学解题，通过代入法，逆向思维等特殊方法解决剩下几题，用想象力解决最后一题，我们最终得分能拿到110-120分。这样子便是我们实力不够的情况下最优解题方法了。

动态规划也属于寻找最优解问题，但是需要我们找出最优解的结构，进而退出其递归公式，最后通过自定向下递归或者自底向上备忘录的办法求解。分治旨在将问题规模不断缩小到便于解决的规模，而动态规划旨在找出最优解的递归函数。
同样是数学考试的例子，假设有n道题，并且你可以无数次尝试解答该试卷，采用不同的解题路线以寻求最高分，设每道题你能得到的的分数为 P(i) 1<=I<=n, 你的最优解为i1，i2, i3,…ik
r = P(i1) + p(i2) + … + p(ik)
r_n = max(p(i) + r_n-i)