这次,我绝对不会再做预测了,绝不可能被打脸
一、基本概念:
1、组合最优化:又称为离散最优化通过对数学方法的研究去寻找离散事件的最优编排、分组、次序或筛选等。可用数学模型表述为:
min f(x)
s.t. g(x)≥0,
x ∈ D
2、组合最优化问题:在给定有限集合的所有具备某些特性的子集族中,寻找使某种指标达到最优的子集的问题。
3、组合最优化问题的目标通常是从组合问题的可行解集中求出最优解
4、算法:一步步求解问题的通用程序,它是解决问题的程序步骤的一个清晰描述
5、定型算法:算法从前一步到后一步的运行是由当时状态唯一确定的
6、算法能解决问题:一个算法,它对问题任意一个给定实例,在有限步之后,一定能得到该实例的答案
7、近似算法:对于一个优化问题,给定任意一个实例,算法总能找到一个可行解
8、最优算法:对于一个优化问题,给定任意一个实例,算法总能找到一个可行解,且这个可行解的目标值总等于最优解值
9、计算复杂性:用算法中的加、减、乘、除和比较等基本运算的总次数(计算时间)C(I)同实例I在计算机计算时的二进制输入数据(输入规模/长度d(I))的大小关系:C(I) = f(d(I))
10、判定问题:一个问题的每一个实例只有“是”或“否”两种答案
11、多项式转换(变换):通过一个算法将两个问题的两个实例之间实现了转换,使实例的解一一对应,即将输入转换为输入,并且得到的结果相对应
12、多项式归约:在多项式时间内,将问题1的输入转换为问题2的输入,则成问题1归约为问题2
13、NP难问题:对于判定问题A,若NP中的任何一个问题可在多项式时间归约为判定问题A,则称A为NP困难问题
14、cook定理的NPC证明:NP中的任何一个问题可在多项式时间内归约为SAT
15、不确定一维搜索:
对于一元函数φ(α),精确一维搜索的条件为φ ’(αk)=0
不精确一维搜索的条件φ ’(αk)≈0,或 |φ ’(αk) | ≤ σ
实际计算中上式不好控制,一般的方法是|φ ’(αk) / φ ’(0) | ≤ σ
16、凸集:
对于一个数集合D,对于其中的任何两个数x和y,构成一个点,以及我们所选的任何实数a,0<a<1,都有
a*x+(1-a)*y∈D
则证明集合D是一个凸集
**性质1:**有限个(或者无限个)凸集的交集为凸集
**性质2:**假设D是凸集,β是一个实数,则下面的集合是凸集
β*D={y|y=β*x, x∈D}
**性质3:**两个凸集的和集是凸集
D1+D2={y|y=x+z,x∈D1,z∈D2}
**推论1:**凸集的线性组合是凸集
**推论2:**凸集中任意有限个点的凸组合仍然在该凸集中
17、极点:
对于一个凸集D中的x,如果D中不存在两个相异的数y,z及某一个实数a,0<a<1,使得
x=α*y+(1-α)*z
则x为D的极点
**性质1:**若D={x ∈Rn| ||x||≤a}(a>0),则||x||=a上的点均为极点
证明:设||x||=a,若存在y,z ∈D及α∈(0,1),使
得x=αy+(1-α)z.则
a2=||x||2=(αy+(1-α)z,αy+(1-α)z)
≤α2||y||2+(1-α)2||z||2+2α (1-α)||y||||z||≤a2
不等式取等号,必须||y||=||z||=a,且( y,z ) =||y||||z||,
容易证明y=z=x,根据定义可知,x为极点.
18、凸函数:
设函数f(x)定义在凸集D上,如果对应任意的x,y∈D,及任意的a∈[0,1]都有
f (α x+(1-α)y) ≤ α f(x)+(1-α) f (y)
则f(x)为凸集D上的凸函数
同理,有严格凸函数的定义
设函数f (x)定义在凸集D上,若对任意的x,y∈D,x≠y,及任意的α ∈(0,1)都有
f (α x+(1-α)y) < α f(x)+(1-α) f (y)
则称函数f (x)为凸集D上的严格凸函数
最常见的严格凸函数是二次函数y=x^2
19、线性规划一般形式:
min(max) c1x1+c2x2+···+cnxn
s.t. a11x1+a12x2+···+a1nxn≥(或≤,=)b1
a21x1+a22x2+···+a2nxn(或≤,=)b2
··· ···
am1x1+am2x2+···+amnxn(或≤,=)bm
x1,x2,···,xn≥0
20、线性规划的标准形式:
min c1x1+c2x2+···+cnxn
s.t. a11x1+a12x2+···+a1nxn=b1
a21x1+a22x2+···+a2nxn=b2
··· ···
am1x1+am2x2+···+amnxn=bm
x1,x2,···,xn≥0
其中bi ≥0.
可以看到,只要将一般形式的大于号或者小于号全部去掉,用等号代替,就可以得到线性规划的标准型
21、矩阵向量形式的标准型
min cTx
(LP) s.t. Ax=b
x≥0
其中
c=(c1,c2,···,cn)T,x=(x1,x2,···,xn)T,b=(b1,b2,···,bm)T

其中,c:是价格向量,A是约束矩阵,b:是右端向量
记A=(p1,p2,··· ,pn),其中pj=(a1j,a2j,···,amj)T,线性规划(LP)又可以表示为
min cT x
(LP) s.t. Σxj*pj=b 从j=1到n求和
xj≥0,j=1,2,...,n
22、线性规划解的情况
满足约束条件的向量x是可行解,全体可行解构成可行域D.
D= Φ 时,称线性规划无可行解;
D≠ Φ 时但目标函数无下界时,称线性规划(LP)无界或无最优解;
D≠ Φ 时若目标函数有下界,可以证明线性规划(LP)必有最优解.
23、线性规划基本概念
设约束矩阵A的秩为m (行满秩),且m≤n,则A中必存在m阶非奇异子阵B,不妨设
B=(p1,p2,···,pm)
称B为线性规划问题(LP)的一个基矩阵,或称为基,基矩阵中的列向量称为基向量,对应的变量称为基变量,其余变量称为非基变量。
24、基解
在约束方程组取定基矩阵
B=(p1,p2,···,pm)
之后,令非基变量均为0,得到的方程组
p1x1+p2x2+···+pmxm=b
有唯一解,这样得到约束方程组的一个解向量
x=(x1,x2,··· xm)T
通过这种方法得到的满足约束方程组的解称为基矩阵B对应的基解。
线性规划 (LP)的基解个数不会超过n关于m的组合
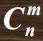
如果基解又满足非负条件,则称之为基可行解,此时的基B称为可行基
基可行解中非零分量的个数不会超过m,
若基可行解中非零分量的个数恰为m,称此基可行解为非退化的基可行解,否则称为退化的基可行解.
若一个线性规划的所有基可行解都是非退化的,称此线性规划是非退化的
简单地将,就是我们从我们的约束矩阵A中找到了一个基矩阵,通过这个基矩阵,我们可以将我们原本的表达式中的部分x变量变为0,然后得到一个新的表达式,这个表达式就是我们约束方程的一个解向量,这个解向量的解就是基解。而针对这个基解,如果基解大于0,就是一个可行解,如果这个可行解中的x的个数正好为x的总数m,说明没有一个x变量变为0,这个可行解就是不可退化的,也就是我们能够用的可行解。
25、线性规划基本定理:
定理1:设x是标准型线性规划(LP)的可行解,x为(LP)的基可行解的充要条件是,x的正分量对应的系数列向量线性无关。
定理2:设x是标准型线性规划(LP)的可行解,x为 (LP)的基可行解的充要条件是,x为可行域D的极点。
推论:线性规划(LP)的可行域D={x|Ax=b,x≥0}最多具有有限个极点,但基可行解与极点并不是一一对应的。
简单地将,我们计算基可行解得到了变量x的解向量,这个响亮如果只是几个相同值得顺序调换,比方说(5,0,0,5,12)与(0,5,0,5,12),就对应着同一个极点。
定理3:若线性规划(LP)存在可行解,则它一定存在基可行解。
定理4:若线性规划(LP)存在最优解,则必存在基可行解是最优解。
二、问题
1、0-1背包问题
可化为:
求最大的Σcixi
条件是Σaixi≤h,即背包容量
且xi∈{0,1},表示物体只能装入或者不装入
2、平行机排序问题
可化为:
求最小的ΣΣcijtj,tj为任务完成所需要的时间
条件是Σcij=1且Σcij=1,即每个任务仅执行一次
且cij∈{0,1},表示任务要么执行要么不执行
3、运输问题
可化为
求最小的ΣΣcijxij
条件是Σxij=ai,即提供数量
Σxij=bj,即使用数量
xij≥0
4、生产计划问题
求最大的Σcjxj
条件是Σaijxj≤bi,即资源需要够用
xj≥dj,即不少于bj的量
5、指派问题
求最小的ΣΣcij*xij
条件是Σxij=1且Σxij=1,即每个人只负责一个任务
xij∈{0,1},即要么负责要么不负责
三、常用算法
期中之前,我们总共学过六种重要算法如下:
①进退法,用于求初始区间
②二分法,用于在可用导数的情况下求解精确搜索
③fibonacci法,用于求解精确搜索
④二次插值法,用于求解精确搜索
⑤黄金分割方法,用于求解精确搜索
⑥frank wolf算法,用于求解模糊搜索
前五种本人已经彻底分析完毕,可以再我的博客中找到,下面进行简单讲解:
1、迭代算法:选取一个初始可行点,从此出发,以此产生一个可行点列
2、下降算法:在迭代算法中要求f(x+1)<f(x)
3、黄金分割法:想要求得峰值所在的区间,所以每次求得的假设区间端点是x1=a+0.382(b-a)和x2=a+0.618(b-a),要么选择区间[a,x2],要么是[x1,b],要么是[x1,x2],具体看f(x1)和f(x2)的取值,如果f(x1)<f(x2),说明x1更靠近最低点,但由于x1不能保证在左侧还是右侧,所以选择x2,即区间变化为[a,x2];如果f(x1)>f(x2),说明x2更靠近最低点,但由于x2不能保证在左侧还是右侧,则选择x1,即区间变化为[x1,b];如果f(x1)=f(x2),说明峰值在x1和x2之间,即区间变化为[x1,x2]。直到区间长度小于精度的时候,终止。
黄金分割法和fibonacci非常相似,在这里不做单独解释。

4、fibonacci法:通过fibonacci数列逼近0.618的特性,从1,2,3开始,每次都取n1=f(n-2)/f(n),n2=f(n-1)/f(n)作为新区间的两端,然后和黄金分割法一样进行分析。每次求得的假设区间端点是x1=a+n1(b-a)和x2=a+n2(b-a),要么选择区间[a,x2],要么是[x1,b],要么是[x1,x2],具体看f(x1)和f(x2)的取值,如果f(x1)<f(x2),说明x1更靠近最低点,但由于x1不能保证在左侧还是右侧,所以选择x2,即区间变化为[a,x2];如果f(x1)>f(x2),说明x2更靠近最低点,但由于x2不能保证在左侧还是右侧,则选择x1,即区间变化为[x1,b];如果f(x1)=f(x2),说明峰值在x1和x2之间,即区间变化为[x1,x2]。直到区间长度小于精度的时候,终止。注意,每次需要找到下一个fibonacci数,对n1和n2进行更新。博客链接:fibonacci法
5、进退法:
注意,进退法不是用来在单峰函数中找最小值得方法,而是在多峰函数中找到单峰区间的方法!!
通过确定步长,然后不断迈步,直到得到一个区间[x0,x2],由于需要直到峰值在区间内,所以需要设定一个x1,让f(x1)<f(x0)且f(x1)<f(x2)。博客链接:进退法
6、二分法:
每次将区间缩小为原来的1/2,每次取c=(a+b)/2,对f( c )求导数,
如果f ’( c )>0,则以[a,c]代替[a,b]作为新区间
如果f ’( c )<0,则以[c,b]代替[a,b]作为新区间
博客链接:二分法
7、二次插值法:
所谓二次插值法,是通过二次函数去模拟我们所得到的的单峰函数,用这个二次函数的极小点作为原来函数的极小点
如果这个极小点的横坐标已经满足了精度的要求,就停止运算
算法步骤如下:
1、设x0,x1,x2三点,其中x0=a,x1=(a+b)/2,x2=b。
2、计算以(x0,f(x0))、(x1,f(x1))、(x2,f(x2)),并以此三点为值求得一个二次函数,计算此二次函数的极值点x=-b/2a,到第三步
3、如果极值点x与x1的差值小于精度,说明已经达到了精度,可以终止,否则转第四步
4、将x0,x1,x2,x进行排序,如果f(x1)>f(x),则说明x更接近最小值,我们选靠近x的两个点,并对x1,x0,x2进行更新:x1=x,x0=小,x2=大,然后回到第二步;否则,说明x1更接近最小值,我们选靠近x1的两个点,并对x0,x2进行更新:x0=小,x2=大,然后返回第二步
博客链接:二次插值法
期中之后,主要学习的算法有:
①凸集判定,博客链接:凸集&凸函数
②线性规划,博客链接:线性规划
③单纯形方法,博客链接:单纯形方法
本人均写出了自己的代码,各位可以从我的博客中找到,下面进行简单的讲解。
1、凸函数判定:
设函数f(x)定义在凸集D上,如果对应任意的x,y∈D,及任意的a∈[0,1]都有
f (α x+(1-α)y) ≤ α f(x)+(1-α) f (y)
则f(x)为凸集D上的凸函数
同理,有严格凸函数的定义
设函数f (x)定义在凸集D上,若对任意的x,y∈D,x≠y,及任意的α ∈(0,1)都有
f (α x+(1-α)y) < α f(x)+(1-α) f (y)
则称函数f (x)为凸集D上的严格凸函数
最常见的严格凸函数是二次函数y=x^2
**举例:**设f (x)=(x–1)^2,试证明f(x)在(–∞,+∞)上是严格凸函数.
证明:设x,y∈ R,且x≠y, α∈(0,1)都有
f (αx+(1-α)y)-(α f (x) +(1-α)f (y))
=(αx+(1-α)y-1)2-α (x-1)2-(1-α) (y-1)2
= –α (1-α)(x-y)2<0
因此f(x)在(–∞,+∞)上是严格凸函数.
2、判定可行域为凸集:
线性规划问题
min cTx
(LP) s.t. Ax=b
x≥0
的可行域D为凸集.
证明 任取x,y ∈ D,则有
Ax=b,x≥0, Ay=b,y≥0
对任意的α ∈ [0,1],设
z=αx+(1-α)y,则z≥0,且
Az=A(αx+(1-α)y)
=αAx+(1-α)Ay
=αb+(1-α)b
=b
因此z ∈ D
D为凸集.
3、线性规划一般形式转化为标准型
即如何将我们的线性规划的大于号小于号去掉
首先,将极大转换为极小,如求最大的f(x)相当于求最小的-f(x)
max f(x) → min –f(x)
然后,根据下面的公式
Σaij*xj≤bi
令xn+i=bi-Σaij*xj
则有xn+i≥0,Σaij*xj+xn+i=bi
最后,将自由变量xj转化,引入非负变量xj’和xj’’
xj’≥0,xj’’≥0
令xj=xj’-xj”
**举例:**我们想要将如下线性规划转化为标准型
min y=2x1-x2-3x3
s.t. x1+x2+x3≤7
x1-x2+x3≥2
-3x1-x2+2x3=5
x1,x2≥0,x3是自由变量
证明:
令 x4=7-(x1+x2+x3),
x5=(x1-x2+x3)-2,
再令
x3=x3’-x3’’,
得到标准型
min y=2x1-x2-3x3’+3x3’’
s.t. x1+x2+x3’-x3’’+x4=7
x1-x2+x3’-x3’’-x5=2
-3x1-x2+2x3’-2x3’’=5
x1,x2,x3’,x3’’,x4,x5≥0
我们可以看到,首先,对于我们的条件不等式,我们可以将他全部转化为:
表达式≥0
的形式,然后用一个新的变量来代替表达式,如x4=表达式
然后,对于我们的自由变量,将其转化为两个正数的差值
最终,我们就可以得到我们的标准型线性规划。
这是重点,复习的时候需要认真看一下,不难,能看懂,相信自己,奥利给
4、求基解
基解
在约束方程组取定基矩阵
B=(p1,p2,···,pm)
之后,令非基变量均为0,得到的方程组
p1x1+p2x2+···+pmxm=b
有唯一解,这样得到约束方程组的一个解向量
x=(x1,x2,··· xm)T
通过这种方法得到的满足约束方程组的解称为基矩阵B对应的基解。
线性规划 (LP)的基解个数不会超过n关于m的组合
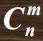
如果基解又满足非负条件,则称之为基可行解,此时的基B称为可行基
基可行解中非零分量的个数不会超过m,
若基可行解中非零分量的个数恰为m,称此基可行解为非退化的基可行解,否则称为退化的基可行解.
若一个线性规划的所有基可行解都是非退化的,称此线性规划是非退化的
简单地将,就是我们从我们的约束矩阵A中找到了一个基矩阵,通过这个基矩阵,我们可以将我们原本的表达式中的部分x变量变为0,然后得到一个新的表达式,这个表达式就是我们约束方程的一个解向量,这个解向量的解就是基解。而针对这个基解,如果基解大于0,就是一个可行解,如果这个可行解中的x的个数正好为x的总数m,说明没有一个x变量变为0,这个可行解就是不可退化的,也就是我们能够用的可行解。
举个例子:考虑线性规划
min 2x1-x2
s.t. x1+x2+x3 =5
-x1-x2 +x4 =0
2x1+2x2+x5=22
x1,x2,x3,x4,x5≥0
我们求一下这个线性规划最多有多少个基解,并求出所有的基解,极其对应的基,并判断是否可以退化。
证明:
首先呢,我们知道这是一个标准型线性规划,
也就是说我们不需要再进行转化了,而我们可以
看到,总共有x1..x5五个变量,所以n为5,而我
们却只有3个约束条件,说明m为3,取组合我们
可以计算出来,最多只有10个基解
实际上,由于我们要求的是与x1和x2有关的表达
式的最小值,也就是说x1与x2是线性相关的,也
就是说我们可以不考虑x1与x2同时出现的情况。
我们先列出所有的基可行解:
(p1,p2,p3)可舍去
(p1,p2,p4)可舍去
(p1,p2,p5)可舍去
(p1,p3,p4)
(p1,p3,p5)
(p1,p4,p5)
(p2,p3,p4)
(p2,p3,p5)
(p2,p4,p5)
(p3,p4,p5)
由此我们可以看到,实际上只用考虑7个基解
我们将这7个基解的对应的解求出来
比方说对(p1,p3,p4),我们就将上述三个条件中的p2与p5置零
我们可以得到如下的方程组
x1+0+x3=5
-x1-0+x4=0
2*x1+2*0+0=22
我们可以解得x1=11,x3=-6,x4=11
所以其对应的解向量就是(11,0,-6,11,0)
由于基解中有负值,所以不可行
同理,我们计算所有的基解的解向量,最终得到如下结果:
(p1,p3,p4),(11,0,-6,11,0)T不可行
(p1,p3,p5),(0,0,5,0,22)T退化
(p1,p4,p5),(5,0,0,5,12)T非退化
(p2,p3,p4),(0,11,-6,11,0)T不可行
(p2,p3,p5),(0,0,5,0,22)T退化
(p2,p4,p5),(0,5,0,5,12)T非退化
(p3,p4,p5),(0,0,5,0,22)T退化
5、单纯形方法:
首先,讲讲思路
我们之前通过求基解的方式得到了可行域的极点(可用的极点),而且我们知道在我们所有求到的极点中必定有一个最优解,我们只需要逐个比较就可以了。
但有些时候,时间开销会非常大,这种方法并不一定合适。
我们于是可以换个思路:
若从某一基本可行解出发,每次总是寻求比上一个更“好”的基本可行解,直至找到最优解。这样就可以大大减少计算量,其实这样的思想应用在非常多的地方,比如梯度下降等等。
于是,我们需要解决下面这三个问题:
(1) 如何判断当前的基本可行解是最优解(迭代终点);
(2) 如何寻找下一个改善的基本可行解(迭代关系式);
(3) 如何得到一个初始的基本可行解(迭代起点);
于是,就有了我们的单纯形方法:
基本过程:
第一步:构造一个初始的基本可行解。
第二步:判断当前基本可行解是否为最优解。
第三步:若当前解不是最优解,则要进行基变换迭代到下一个基本可行解。
下面是我解一道题的手写过程,抱歉,字比较丑~



祝愿各位~~还有我,我,我!!!~~考个好成绩
