凸优化
生活中的凸随处可见,所谓凸就是高于周围的意思。数学中的凸与之类似,但有更加丰富的内涵。在弄清凸规划之前首先要理解什么是凸集以及什么是凸函数。
凸集
定义
定义 给定 ∀ x , y ∈ C \forall x,y \in C ∀x,y∈C 及 θ ∈ ( 0 , 1 ) \theta \in(0,1) θ∈(0,1),若点 θ x + ( 1 − θ ) y ∈ C \theta x +(1-\theta)y \in C θx+(1−θ)y∈C ,则称 R n \mathbb{R}^n Rn 中集合 C C C 是凸的(convex)。进一步,对 ∀ a > 0 , x ∈ C \forall a>0,x \in C ∀a>0,x∈C,都有 a x ∈ C ax\in C ax∈C,则称 C C C 为凸锥(convex cone)。
几何解释:连接集合中任两点的线段仍含在该集合中。
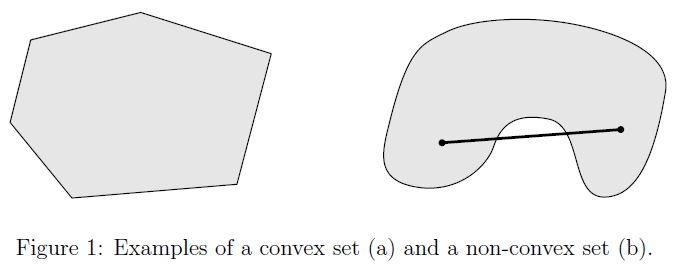
性质
由凸集的定义,我们可以得到如下性质:
性质 若 C , D C,D C,D 为凸集, β \beta β 为实数,则
(1) 任意多个凸集的交是凸集;
(2) 集合 C + D = { x : x = c + d , c ∈ C , d ∈ D } C+D=\{x:x=c+d,c\in C,d\in D\} C+D={ x:x=c+d,c∈C,d∈D} 是凸集;
(3) 设 β \beta β 是实数,则集合 β C = { x : x = β c , c ∈ C } \beta C = \{x:x=\beta c ,c\in C\} βC={ x:x=βc,c∈C} 是凸集。
凸函数
有了凸集的定义,下面我们给出凸函数的定义。
定义
定义 设 f f f 是定义在凸集 C C C 上的函数,对 ∀ x 0 , x 1 ∈ C \forall x_0,x_1 \in C ∀x0,x1∈C,有
f θ ≤ ( 1 − θ ) x 0 + θ x 1 , θ ∈ ( 0 , 1 ) f_{\theta} \leq (1-\theta) x_0 + \theta x_1, \theta\in(0,1) fθ≤(1−θ)x0+θx1,θ∈(0,1)
其中 f θ = f ( x θ ) f_{\theta} = f(x_{\theta}) fθ=f(xθ),且
x θ = ( 1 − θ ) x 0 + θ x 1 x_{\theta} = (1-\theta) x_0 + \theta x_1 xθ=(1−θ)x0+θx1
则函数 f f f 是凸的。
几何解释:凸组合的函数值小于函数值的凸组合。
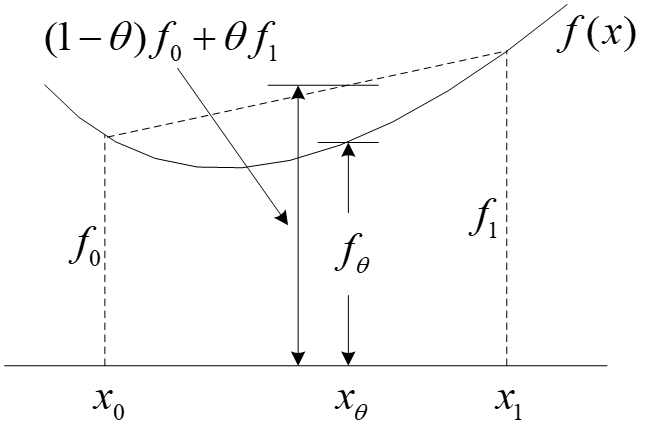
定理 若 C C C 为凸集, f ( x ) f(x) f(x) 在 C C C 上可微,其凸性的一个等价定义为,对 ∀ x 0 , x 1 ∈ C \forall x_0,x_1 \in C ∀x0,x1∈C,有
f 1 ≥ f 0 + ( x 1 − x 0 ) T ∇ f n f_1 \geq f_0 + (x_1-x_0)^T \nabla f_n f1≥f0+(x1−x0)T∇fn
几何解释: f f f 的图形位于在 x 0 x_0 x0 处切线的上方。称这样的切线为凸函数的支撑超平面。
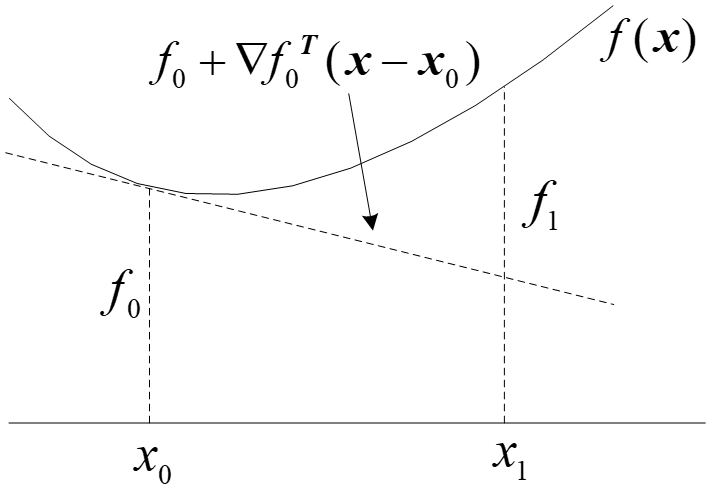
特别地,若上述不等式严格成立时,则为严格凸函数。与凸函数相对的则是凹函数了,在此不再赘述。
性质
有了凸函数的定义,易得
- 若 f i ( x ) , i = 1 , 2 , ⋯ , m f_i(x), i = 1,2,\cdots,m fi(x),i=1,2,⋯,m 是凸集 C C C 上的凸函数,则它们的非负线性组合仍然是 C C C 上的凸函数。
- 凸函数的 f f f 在凸集 C C C 上的局部极小点是全局极小点。
- 可微凸函数的稳定点是全局极小点。
- 若 f f f 是开凸集 C C C 上的二次连续可微实值函数,则 f f f 凸当且仅当 C C C 中的每个 x x x,满足 ∇ 2 f ( x ) \nabla^2 f(x) ∇2f(x) 是半正定的。
凸规划
有了凸集和凸函数的定义,就可以来定义凸规划了。
定义
定义 广义上,凸集 Ω ⊆ R n \Omega \subseteq \mathbb{R}^n Ω⊆Rn 上极小化凸函数 f ( x ) f(x) f(x),表示为
min x ∈ R n f ( x ) s . t . x ∈ Ω : = { x ∣ c i ( x ) ≤ 0 , i = 1 , 2 , ⋯ , m } \begin{aligned} \min_{x \in \mathbb{R}^n} ~~& f(x)\\ \mathrm{s.t.}~~&x\in \Omega := \{x|c_i(x)\leq 0 ,i = 1,2,\cdots,m\} \end{aligned} x∈Rnmin s.t. f(x)x∈Ω:={ x∣ci(x)≤0,i=1,2,⋯,m}
其中 f ( x ) f(x) f(x) 与 c i ( x ) ( i = 1 , 2 , ⋯ , m ) c_i(x)~(i = 1,2,\cdots,m) ci(x) (i=1,2,⋯,m) 为 R n \mathbb{R}^n Rn 上的凸函数。
可行域 Ω \Omega Ω 的凸集结论可以由一下引理证明。
引理 凸函数 f ( x ) f(x) f(x) 的水平集 L γ = { x ∈ d o m f : f ( x ) ≤ γ } L_{\gamma} = \{x\in \mathrm{dom}f:f(x)\leq \gamma\} Lγ={ x∈domf:f(x)≤γ} 对任意 γ ∈ R \gamma \in \mathbb{R} γ∈R 都是凸集。
证明 设 x 0 , x 1 ∈ L x_0,x_1\in L x0,x1∈L, θ ∈ ( 0 , 1 ) \theta \in (0,1) θ∈(0,1), x θ = ( 1 − θ ) x 0 + θ x 1 x_{\theta} = (1-\theta) x_0 + \theta x_1 xθ=(1−θ)x0+θx1,由集合 C C C 凸知 x θ ∈ C x_{\theta} \in C xθ∈C,则
f ( x θ ) ≤ ( 1 − θ ) f 0 + θ f 1 ≤ ( 1 − θ ) γ + θ γ = γ f(x_{\theta}) \leq (1-\theta)f_0 + \theta f_1 \leq (1-\theta) \gamma + \theta\gamma = \gamma f(xθ)≤(1−θ)f0+θf1≤(1−θ)γ+θγ=γ
因此 x θ ∈ L x_{\theta} \in L xθ∈L, L L L 是凸的。
性质
凸性除了保证局部极小点是全局极小点以外,还保证了一阶必要条件是局部极小点的充分条件,不需要正则性假设。
定理 凸规划的任一 KKT 点是全局极小点。
特别地,线性规划是凸规划;如果二次规划中目标函数的 Hessian 阵半正定,则它也是凸规划。
例 考虑问题
min ( x 1 − 3 2 ) 2 + ( x 2 − 1 2 ) 4 s . t . x 1 + x 2 − 1 ≤ 0 x 1 − x 2 − 1 ≤ 0 − x 1 + x 2 − 1 ≤ 0 − x 1 − x 2 − 1 ≤ 0 \begin{aligned} \min~~&(x_1 - \frac{3}{2})^2 +(x_2 - \frac{1}{2})^4\\ \mathrm{s.t.}~~ & x_1 + x_2 - 1 \leq 0\\ &x_1 - x_2 -1 \leq 0 \\ &-x_1 + x_2 - 1 \leq 0 \\ &-x_1 - x_2 - 1 \leq 0 \end{aligned} min s.t. (x1−23)2+(x2−21)4x1+x2−1≤0x1−x2−1≤0−x1+x2−1≤0−x1−x2−1≤0
解 如下图所示,问题的解为 x ∗ = ( 1 , 0 ) T x^* = (1,0)^T x∗=(1,0)T,在该点处,第一个和第二个约束是积极的,分别记为 c 1 , c 2 c_1,c_2 c1,c2,于是
g ∗ = ( − 1 − 1 2 ) , a 1 ∗ = ( 1 1 ) , a 2 ∗ = ( 1 − 1 ) g^* = \begin{pmatrix} -1 \\ -\frac{1}{2} \end{pmatrix}, a_1^* = \begin{pmatrix} 1 \\ 1 \end{pmatrix}, a_2^* = \begin{pmatrix} 1 \\ -1 \end{pmatrix} g∗=(−1−21),a1∗=(11),a2∗=(1−1)
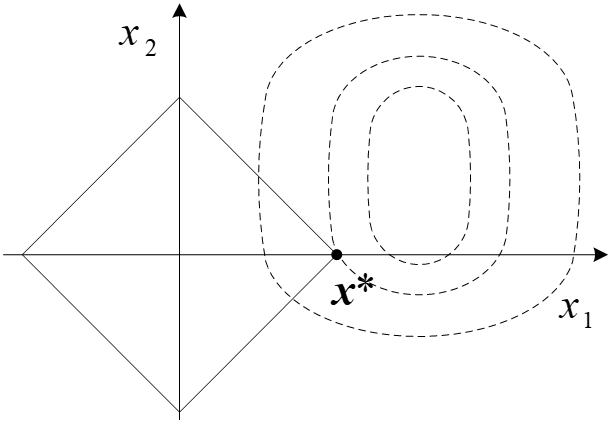
因此,得 Lagrange 乘子
λ ∗ = ( 3 4 , 1 4 , 0 , 0 ) T \lambda^* = \begin{pmatrix} \frac{3}{4},\frac{1}{4}, 0, 0 \end{pmatrix}^T λ∗=(43,41,0,0)T
又问题是凸规划,因此 x ∗ x^* x∗ 是全局极小点。
然而,凸规划得解不一定是 KKT 点,例如
min x ∈ R 2 x 1 2 + x 2 2 s . t . ( x 1 − 1 ) 2 + ( x 2 − 1 ) 2 ≤ 1 ( x 1 − 1 ) 2 + ( x 2 + 1 ) 2 ≤ 1 \begin{aligned} \min_{x \in \mathbb{R}^2}~~&x_1^2 + x_2^2\\ \mathrm{s.t.}~~ & (x_1 - 1)^2 +(x_2-1)^2 \leq 1 \\ & (x_1 - 1)^2 +(x_2+1)^2 \leq 1 \\ \end{aligned} x∈R2min s.t. x12+x22(x1−1)2+(x2−1)2≤1(x1−1)2+(x2+1)2≤1
本身是凸规划,但最优解不满足 KKT 条件。