网络流(network-flows)是一种类比水流的解决问题方法,与线性规划密切相关。网络流的理论和应用在不断发展。而我们今天要讲的就是网络流里的一种常见问题——最大流问题。
最大流问题(maximum flow problem),一种组合最优化问题,就是要讨论如何充分利用装置的能力,使得运输的流量最大,以取得最好的效果。求最大流的标号算法最早由福特和福克逊与与1956年提出,20世纪50年代福特(Ford)、(Fulkerson)建立的“网络流理论”,是网络应用的重要组成成分。
再解决这个问题前,我们要先弄懂一些定义:
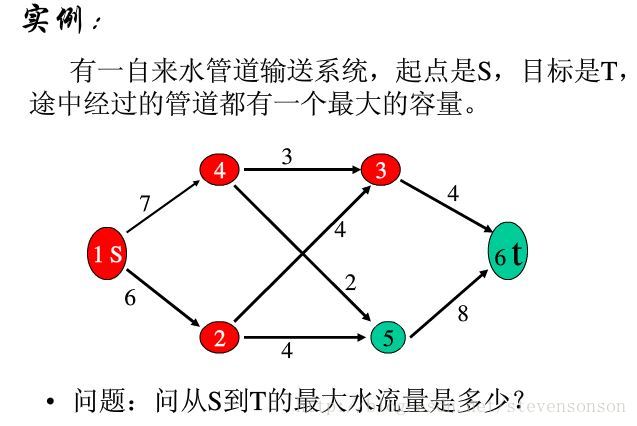
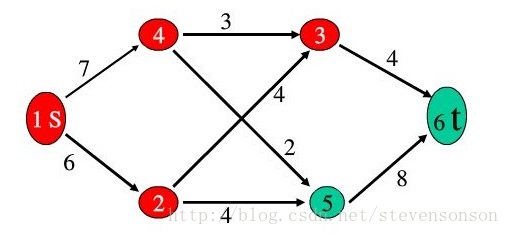
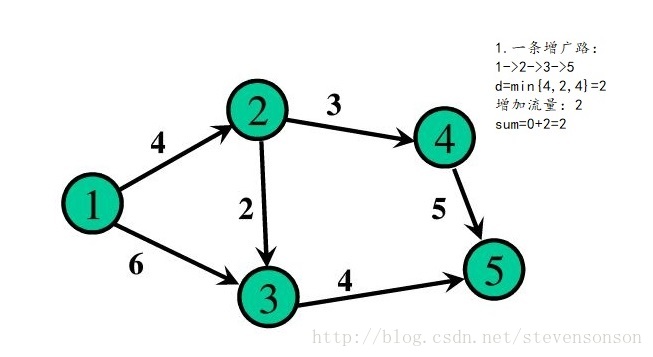
网络流图是一张只有一个源点和汇点的有向图,而最大流就是求源点到汇点间的最大水流量,下图的问题就是一个最基本,经典的最大流问题
二.流量,容量和可行流
对于弧(u,v)来说,流量就是其上流过的水量(我们通常用f(u,v)表示),而容量就是其上可流过的最大水量(我们通常用c(u,v)表示),只要满足f(u,v)<=c(u,v),我们就称流量f(u,v)是可行流(对于最大流问题而言,所有管道上的流量必须都是可行流)。
三.增广路
如果一条路上的所有边均满足:
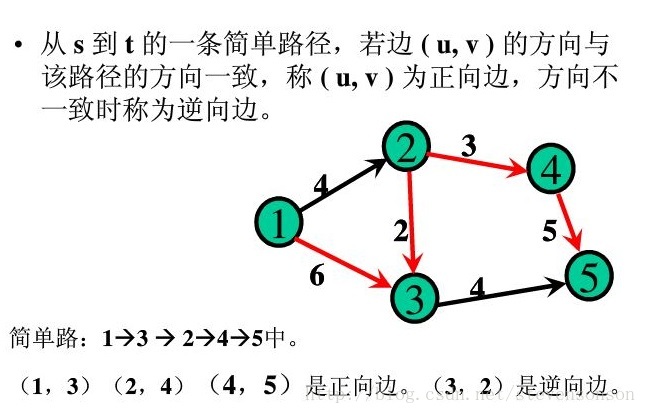
正向边: f(u,v)< c(u,v) ——– 反向边:f(u,v)> 0
假如有这么一条路,这条路从源点开始一直一段一段的连到了汇点,并且,这条路上的每一段都满足流量<容量,注意,是严格的<,而不是<=。那么,我们一定能找到这条路上的每一段的(容量-流量)的值当中的最小值delta。我们把这条路上每一段的流量都加上这个delta,一定可以保证这个流依然是可行流。这样我们就得到了一个更大的流,他的流量是之前的流量+delta,而这条路就叫做增广路. From 网络流(Network Flow)
则我们称这条路径为一条增广路径,简称增广路。
好了,弄懂了一些定义,接下来就可以介绍著名的Ford-Fulkerson算法了。
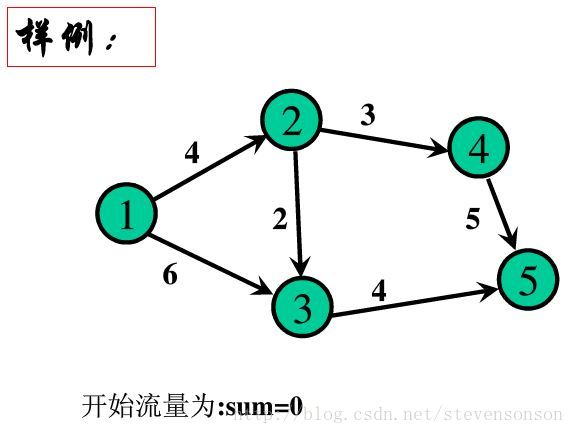
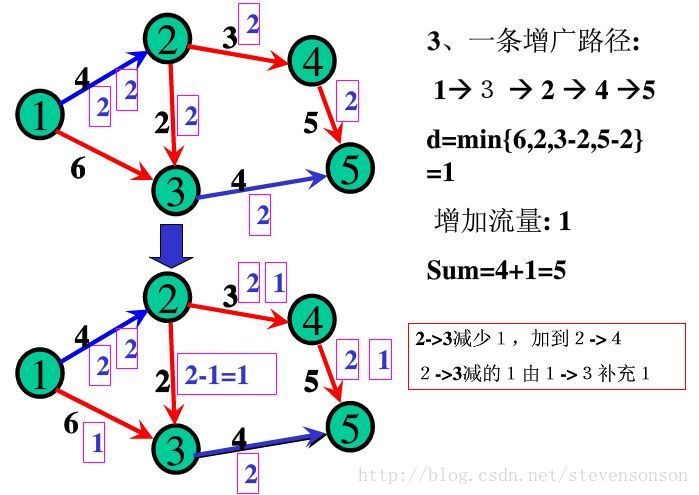
如图所示,如果我们每次都找出一条增广路,只要这条增广路经过汇点,那说明此时水流还可以增加,增加的量为d(d=min(d,c(u,v)-f(u,v))或d=min(d,f(u,v)))。
我们可以这样理解:对于每一条正向边,他能添加的最大水流为c(u,v)-f(u,v)。而对于反向边来说,当正向边上的水流增多时,反向边自身的反向水流会减少,而其能减少的最多水量为f(u,v)。由于要保证添加水流之后,所有的f(u,v)都是可行流,所以我们取最小值。
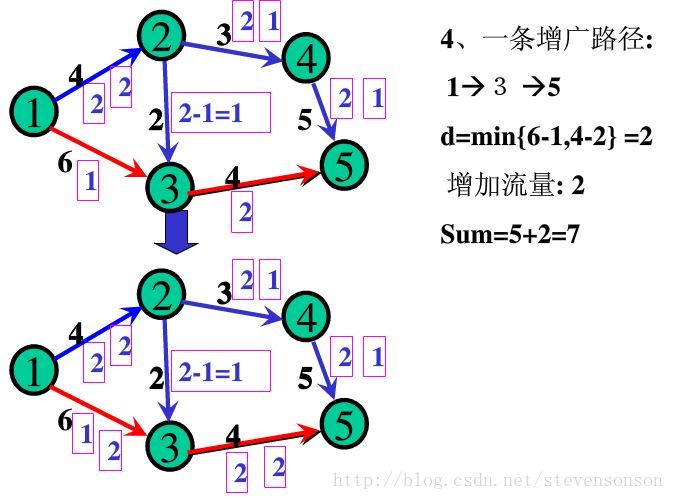
增加之后,我们要更新流量,每条正向边+d,每条反向边-d即可。
既然这样,我们的思路就是:
1.找出一条增广路径 ——2.修改其上点的值——3.继续重复1,直至找不出增广路。则此时源点的汇出量即为所求的最大流。
那么上代码:
#include<bits/stdc++.h>
#include<vector>
#define maxn 1200
#define INF 2e9
using namespace std;
int i,j,k,n,m,h,t,tot,ans,st,en;
struct node{
int c,f;
}edge[maxn][maxn];
int flag[maxn],pre[maxn],alpha[maxn],q[maxn],v;
int read(){
char c;int x;while(c=getchar(),c<'0'||c>'9');x=c-'0';
while(c=getchar(),c>='0'&&c<='9') x=x*10+c-'0';return x;
}
void bfs(){
memset(flag,0xff,sizeof(flag));memset(pre,0xff,sizeof(pre));memset(alpha,0xff,sizeof(alpha));
flag[st]=0;pre[st]=0;alpha[st]=INF;h=0,t=1;q[t]=st;
while(h<t){
h++;v=q[h];
for(int i=1;i<=n;i++){
if(flag[i]==-1){
if(edge[v][i].c<INF&&edge[v][i].f<edge[v][i].c){
flag[i]=0;pre[i]=v;alpha[i]=min(alpha[v],edge[v][i].c-edge[v][i].f);q[++t]=i;
}
else if(edge[i][v].c<INF&&edge[i][v].f>0){
flag[i]=0;pre[i]=-v;alpha[i]=min(alpha[v],edge[i][v].f);q[++t]=i;
}
}
}
flag[v]=1;
}
}
void Ford_Fulkerson(){
while(1){
bfs();
if(alpha[en]==0||flag[en]==-1){
break;
}
int k1=en,k2=abs(pre[k1]);int a=alpha[en];
while(1){
if(edge[k2][k1].c<INF) edge[k2][k1].f+=a;
else if(edge[k1][k2].c<INF) edge[k1][k2].f-=a;
if(k2==st) break;
k1=k2;k2=abs(pre[k1]);
}
alpha[en]=0;
}
}
void flow(){
int maxflow=0;
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++){
if(i==st&&edge[i][j].f<INF) maxflow+=edge[i][j].f;
}
printf("%d",maxflow);
}
int main(){
int u,v,c,f;
n=read();m=read();st=read();en=read();
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++) edge[i][j].c=INF,edge[i][j].f=0;
for(int i=1;i<=m;i++){
u=read();v=read();c=read();
edge[u][v].c=c;
}
Ford_Fulkerson();
flow();
return 0;
}