一、\(kd-tree\)是用来干什么的

\(kd-tree\)：KevinDurant-tree，不，不是这个，再来一次

\(kd-tree\)：\(k-dimensional\) 树的简称

英语好的同学就会知道，\(dimensional\)是维度的意思，所以，\(kd-tree\)的字面意思就是：\(k\)维树

在这里，大家应该就知道\(kd-tree\)是用来干嘛的了

没错，是用来维护多维数据和查询多维数据的

在这一点上，多维数据的问题肯定困扰了很多学生，\(kd-tree\)就是专门用来解决这类问题的

但是蒟蒻发现基本主流考法都是考\(2\)维的，所以本文只讲\(2\)维的做法（啪，其实是自己不会多维的）

二、\(kd-tree\)是什么

\(kd-tree\)是一个\(BST\)（二叉搜索树）的变种

\(BST\)是什么？

\(BST\)的左子树的节点的关键字一定小于当前节点的关键字，右子树的节点的关键字一定大于当前节点的关键字

\(BST\)其实是对一个一维的东西进行划分

那么\(kd-tree\)就是对一个\(k\)维的东西进行划分

那么，大家都知道，\(kd-tree\)有\(k\)个关键字（即维度）。

现在我们需要考虑的是，在每一层应该按哪一个关键字来划分？

有一种策略是，计算出每一种维度的方差，挑选出方差最大那一个，这说明在这个维度上每个点分散的最开，所以可以划分得更平衡一点

但是在\(2\)维的情况下，我们一般将\(1,2\)维轮流使用

关于确定好每一层按哪个关键字后，我们就把点按照关键字排序，并取当前数列中的中间那一个，再对它的下一层进行遍历

不懂的我们先按\(2d-tree\)的情况来看看

我们可以看到这个图（手画的不要太难看）
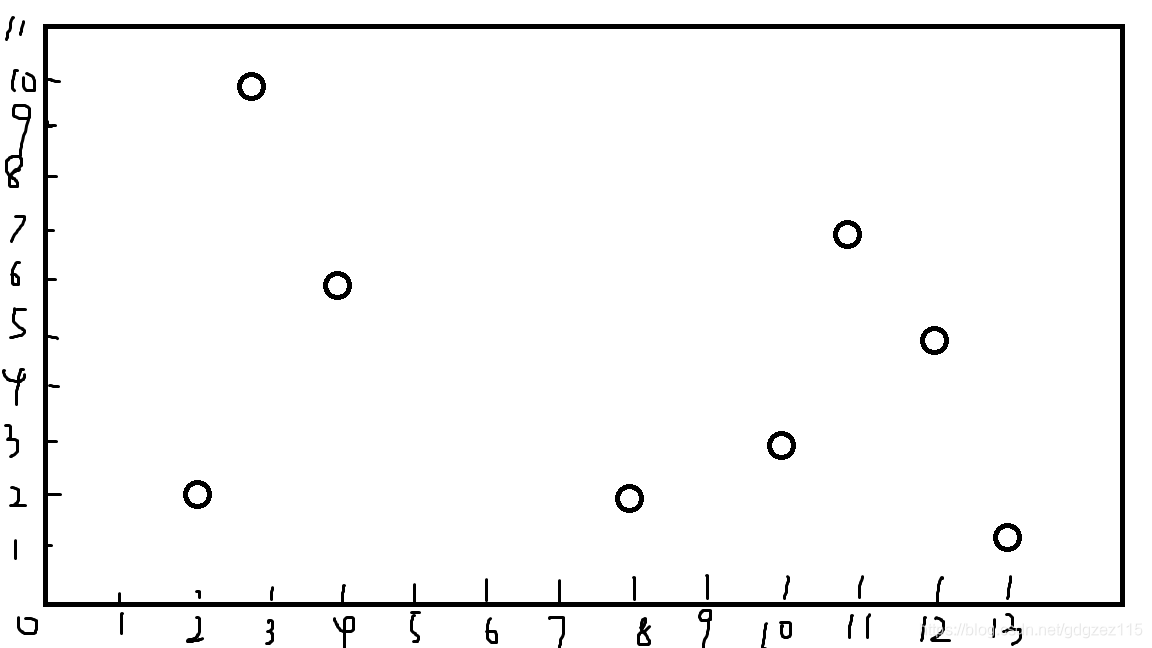
在这里插入图片描述

我们考虑首先按\(x\)来划分，取到最中间一个\((8,2)\)

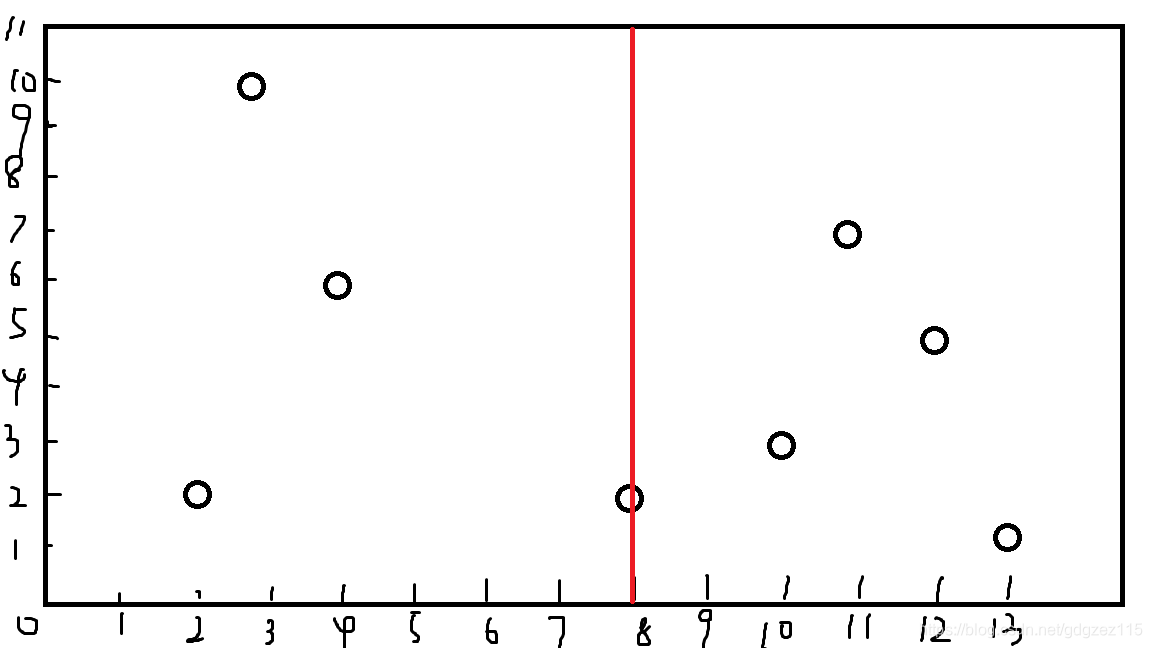
在这里插入图片描述

再按照\(y\)来，取到\((4,6)\)和\((10,3)\)

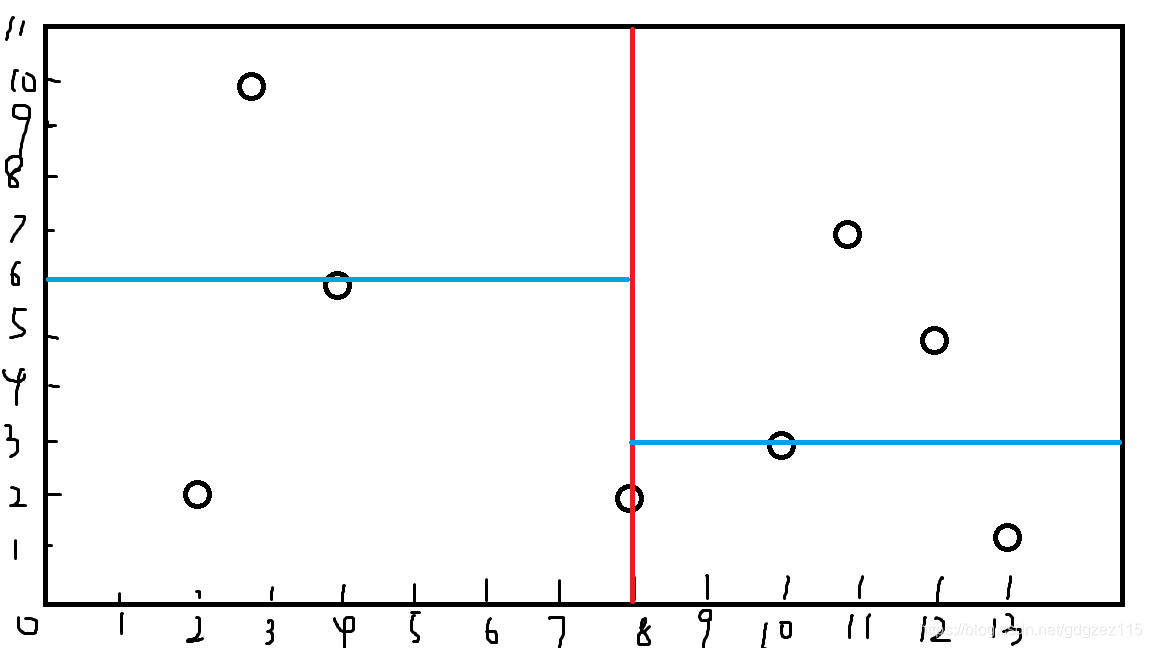
在这里插入图片描述

再按照\(x\)来

此时只需要划分右边的区间，取到\((11,7)\)

在这里插入图片描述

这样，一棵\(2d-tree\)就建好啦，建出来应该是这样的：

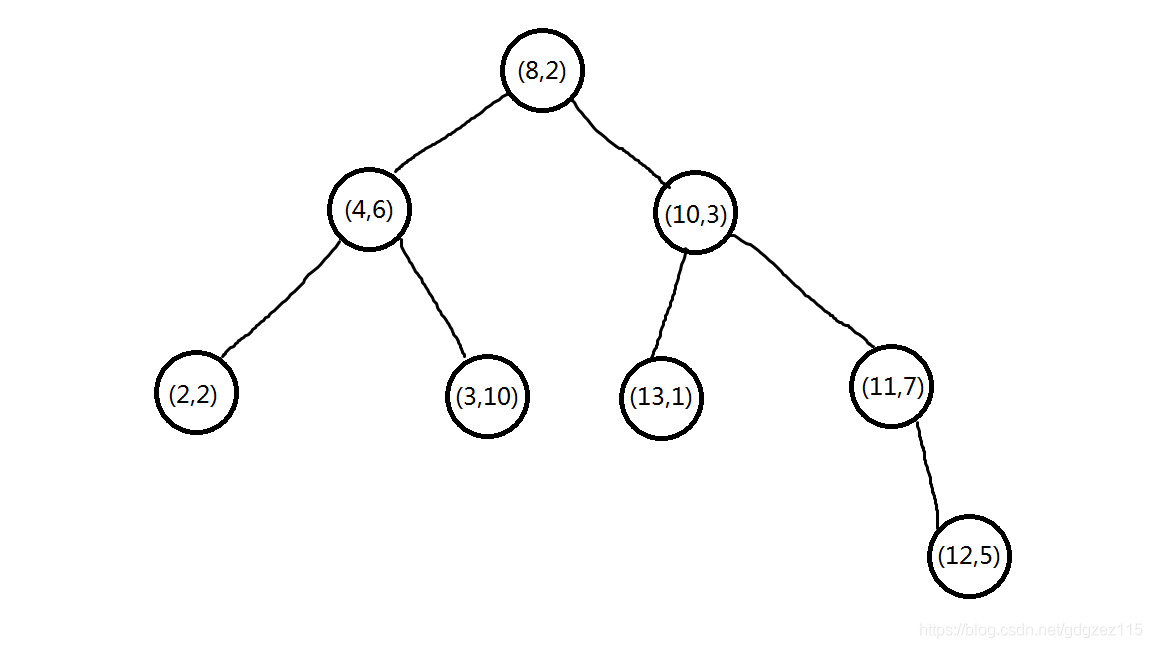
在这里插入图片描述

我们可以发现，这样建出来的\(kd-tree\)因为每次取中间数，所以建出来的树的叶子节点的深度都十分接近，可以近乎平衡，但是，并不是所有情况都可以保证平衡，所以，我们采用如替罪羊树一样的方法将不平衡的子树拍扁重建，这样使得树的高度在\(nlog_{n}\sim n\sqrt{n}\)之间（但是它十分不稳定...）

\(kd-tree\)的建树和原理都已经讲解完毕，大概就是这样一种==平衡+替罪羊树==的思想

三、例题

1.P4148 简单题

Description

内存限制为20MB

你有一个\(N×N\)的棋盘，每个格子内有一个整数，初始时的时候全部为\(0\)，现在需要维护两种操作：

命令参数限制内容
\(1\) \(x\) \(y\) \(A\)
\(1≤x,y≤N\),\(A\)是正整数将格子\(x,y\)里的数字加上\(A\)

\(2\) \(x_{1}\) \(y_{1}\) \(x_{2}\) \(y_{2}\)
\(1≤x1≤x2≤N,1≤y1≤y2≤N\) 输出x1 y1 x2 y2这个矩形内的数字和

3 无终止程序

\(Input\)

输入文件第一行一个正整数\(N\)。
接下来每行一个操作。每条命令除第一个数字之外，
均要异或上一次输出的答案\(lastans\)，初始时\(lastans=0\)。

\(Output\)

对于每个\(2\)操作，输出一个对应的答案。

\(Sample Input\)

4
1 2 3 3
2 1 1 3 3
1 1 1 1
2 1 1 0 7
3

\(Sample Output\)

3
5

\(HINT\)

\(1≤N≤500000\),操作数不超过\(200000\)个，内存限制\(20M\)，保证答案在\(int\)范围内并且解码之后数据仍合法。

Source
练习题　树8-8-KD-tree

思路

一道\(kd-tree\)模板题（~~要不然我为什么要放在第一题~~ ）

我们考虑对于每一个操作\(2\)，我们都将这个节点的\(x,y,val\)打包成一个\(struct\)插入\(kd-tree\)的每一个节点中，并维护五个值：\(maxx,maxy,minx,miny,sum\)，前四个分别代表以这个节点为根节点的子树中的每个节点的\(x,y\)的最大值和最小值，\(sum\)代表以这个节点为根的子树中的权值和

考虑对于操作\(3\)

我们从根节点\(k\)开始向下遍历：

如果以这个子树为根的子树完全不在询问矩阵内，\(return\) \(0\)
如果\(\sim\)完全在询问矩阵内，\(return\) \(t[k].sum\)
如果以上两种情况都不是，说明有一部分在矩阵中，那么我们先判断当前节点\(k\)是否在矩阵中，如果是加上\(k\)自己的权值，再遍历左右子树，将答案求和

细节见代码

#include<bits/stdc++.h>
using namespace std;
const int N=200005;
const double alpha=0.725;
int n,rt,nodetot=0,topp=0,cnt=0;
struct point
{
    int x[2],val;
}p[N];
struct tree
{
    int lc,rc,siz,sum;
    int maxn[2],minn[2];
    point pt;
}t[N];
int WD;
int rub[N];
bool cmp(point a,point b)
{
    return a.x[WD]<b.x[WD];
}
int newnode()
{
    if(topp)return rub[topp--];
    return ++nodetot;
}
void update(int k)
{
    t[k].siz=t[t[k].lc].siz+t[t[k].rc].siz+1;
    t[k].sum=t[t[k].lc].sum+t[t[k].rc].sum+t[k].pt.val;
    for(int i=0;i<=1;i++)
    {
        t[k].maxn[i]=t[k].minn[i]=t[k].pt.x[i];
        if(t[k].lc)
        {
            t[k].maxn[i]=max(t[k].maxn[i],t[t[k].lc].maxn[i]);
            t[k].minn[i]=min(t[k].minn[i],t[t[k].lc].minn[i]);
        }
        if(t[k].rc)
        {
            t[k].maxn[i]=max(t[k].maxn[i],t[t[k].rc].maxn[i]);
            t[k].minn[i]=min(t[k].minn[i],t[t[k].rc].minn[i]);
        }
    }
}
bool bad(int k)//如替罪羊树一样判断是否平衡
{
    return (t[k].siz*alpha<t[t[k].lc].siz||t[k].siz*alpha<t[t[k].rc].siz);
}
void work(int k)
{
    if(t[k].lc)work(t[k].lc);
    p[++cnt]=t[k].pt;
    rub[++topp]=k;//将不用的节点编号存进rub中，节省空间
    if(t[k].rc)work(t[k].rc);
}
int build(int l,int r,int wd)
{
    if(l>r)return 0;
    int mid=(l+r)>>1,k=newnode();
    WD=wd;//每次按照当前维度排序
    nth_element(p+l,p+mid,p+r+1,cmp);
    //这是一个神奇的STL，会使得序列a中[l,r]中的第mid小的元素在第mid位上，但是其他元素并不有序！！！
    //这个STL的时间复杂度为O(n)，这也是我们不使用sort的原因，并且可以去到中位数
    t[k].pt=p[mid];
    t[k].lc=build(l,mid-1,wd^1);
    t[k].rc=build(mid+1,r,wd^1);
    update(k);
    return k;
}
void rebuild(int &k)
{
    cnt=0;
    work(k);//拍扁
    k=build(1,cnt,0);//重建
}
void ins(int &k,point tmp,int wd)
{
    if(!k)//新建节点
    {
        k=newnode();
        t[k].lc=t[k].rc=0;
        t[k].pt=tmp;
        update(k);
        return ;                    
    }
    if(tmp.x[wd]<=t[k].pt.x[wd])ins(t[k].lc,tmp,wd^1);
    else ins(t[k].rc,tmp,wd^1);
    //判断应该插入进左子树还是右子树中
    update(k);
    if(bad(k))rebuild(k);//如果不平衡，拍扁重建
}
bool out(int nx1,int nx2,int ny1,int ny2,int x1,int y1,int x2,int y2)
{
    if(x1>nx2||x2<nx1||y1>ny2||y2<ny1)return 1;
    return 0;
}
bool in(int nx1,int nx2,int ny1,int ny2,int x1,int y1,int x2,int y2)
{
    if(nx1>=x1&&nx2<=x2&&ny1>=y1&&ny2<=y2)return 1;
    return 0;
}
int query(int k,int x1,int y1,int x2,int y2)
{
    if(!k)return 0;
    if(out(t[k].minn[0],t[k].maxn[0],t[k].minn[1],t[k].maxn[1],x1,y1,x2,y2))return 0;
    //完全在矩阵外
    if(in(t[k].minn[0],t[k].maxn[0],t[k].minn[1],t[k].maxn[1],x1,y1,x2,y2))return t[k].sum;
    //完全在矩阵内
    int res=0;
    if(in(t[k].pt.x[0],t[k].pt.x[0],t[k].pt.x[1],t[k].pt.x[1],x1,y1,x2,y2))res+=t[k].pt.val;
    //当前节点在矩阵内
    return query(t[k].lc,x1,y1,x2,y2)+query(t[k].rc,x1,y1,x2,y2)+res;
}
inline int read()
{
    int x=0,f=1;
    char ch=getchar();
    while(!isdigit(ch))
    {
        if(ch=='-')f=-1;
        ch=getchar();
    }
    while(isdigit(ch))
    {
        x=(x<<3)+(x<<1)+(ch^48);
        ch=getchar();
    }
    return x*f;
}
int main()
{
    n=read();
    int op,lastans=0,x,y,a,x1,y1;
    while(1)
    {
        op=read();
        if(op==3)return 0;
        if(op==1)
        {
            x=read(),y=read(),a=read();
            x^=lastans,y^=lastans,a^=lastans;
            ins(rt,(point){x,y,a},0);
        }
        if(op==2)
        {
            x=read(),y=read(),x1=read(),y1=read();
            x^=lastans,y^=lastans,x1^=lastans,y1^=lastans;
            printf("%d\n",lastans=query(rt,x,y,x1,y1));
        }
    }
    return 0;
}
/*
4
1 2 3 3
2 1 1 3 3
1 1 1 1
2 1 1 0 7
3
*/

【模板】kd-tree

一、\(kd-tree\)是用来干什么的

\(kd-tree\)：KevinDurant-tree，不，不是这个，再来一次

\(kd-tree\)：\(k-dimensional\) 树的简称

二、\(kd-tree\)是什么

三、例题

Description

内存限制为20MB

\(Input\)

\(Output\)

\(Sample Input\)

\(Sample Output\)

\(HINT\)

思路

猜你喜欢