好难啊
I 最大流
其实裸的最大流还是很少的,一般需要结合一些其他知识
通常需要进行拆点
$「HNOI2007」紧急疏散evacuate$
我们发现能否撤离显然满足单调性
二分撤离时间,关键是怎么$check$
发现最麻烦的就是每个门同一时刻只能通过一个人
考虑拆点,把一扇门拆成各个时刻的门,并向汇点i连流量为一的边就好了
只需要判断最大流是否等于人数就好了
当然也可以直接枚举时间然后动态建边
II 最小割
最经常出现的知识点
一般的,在某些边的选或不选有联系的情况下需要用到最小割
还经常用到 最大值=全集-最小割
建图方式:
1,原图
$海拔$
仔细阅读题意后可以发现,点的高度只有$0/1$
继续观察我们发现答案就是原图的一个最小割
然而直接跑会$TLE$
引入:对偶图
把平面图的每一个封闭区域看成一个点,如果原图中两个封闭区域有交边就在新图中两个点之间连一条边,值得注意的是,整个平面图外面的区域也是“封闭区域”(即S和T两点)。这样得到一张新的图,就是我们说的对偶图
而对于一张平面图来说,对偶图中的最短路即为原图中的最大流
对于这题来说,相当与已经把平面图给出
那么我们把每条边旋转90°就得到原图的对偶图了
2,抽离题意,观察性质
这方面大多数题都是最大权闭合子图
最大权闭合子图:有 n 个物品, 每个物品有一个 val(整数), 并且每个物品有一个依赖集合, 即选择物品 x,x 所依赖的物品也要选,问权值和的最大值
大多数情况下建图是长这样的
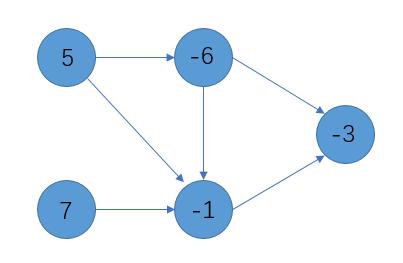
变为
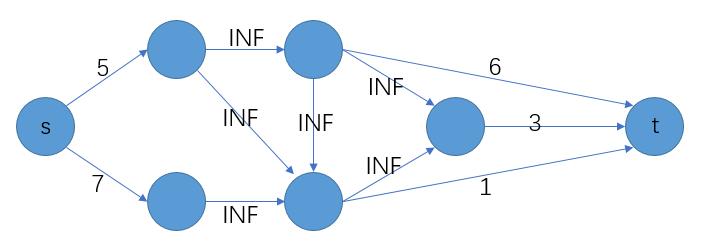
$happiness$
有依赖关系的最大值,看起来很像最大权闭合子图
但是这题里并不是简单的选或不选哪个点,而是选择一个点的归属
我们抛开最大权单独考虑最小割
把$S,T$分别看作$A(文科)$和$B(理科)$
1,$S$向每个点i连流量为$A[i]$的边,每个点向T连流量为B[i]的边
2,新建点$a[i][j]$表示$i,j$同时选文的贡献
3,连接$(a[i][j],i,inf),(a[i][j],j,inf),(S,a[i][j],A[i][j])$
4,新建点b[i][j]表示i,j同时选理的贡献
5,连接$(i,b[i][j],inf),(j,b[i][j],inf),(b[i][j],T,B[i][j])$
跑最大流即可
答案为全集-最大流
$老C的方块$
这题主要考察最小割中分层图的构建
观察四种不合法情况
发现是如下图中黑色和白色点不能共存,或者割掉红色的一个点
拓展到整张图上
我们发现红色的点相互没有干扰,而黑色和白色的格子对于周围的红格子无法共存
考虑这样建图
1,(S,黑格,花费) (白格,T,花费)
2,(左红格,右红格,min(左红格花费,右红格花费))
3,(黑格,左红格,inf) (右红格,白格,inf)
变成了一个很裸的最小割模型
$寿司餐厅$
抽象题意发现是一个依赖模型
又有正负边权,考虑最大权闭合子图
考虑题中的限制关系
1,选$[i,j]$,必须选$[i+1,j]$和$[i,j-1]$
2,负贡献中的cx,可以直接让$b[i][i]$减去$a_{i}$
3,负贡献中的$mx^{2}$,对于每个编号新建一个点,向所有编号为它的点连边
然后按照最大权闭合子图跑就好了
III 费用流
就是网络流中的每条边带上费用
把$bfs$改成$spfa$就好了
主要难点在于抽象出费用流的模型以及分层图的构建
$数字配对$
主要难点在于构建分层图
观察相除为一个质数这条要求,可以得到配对的两个数所含质因子个数奇偶性相反
那么我们可以这样构建分层图
1,对每个数分解指因数,个数为奇数的连边$(S,i,b[i],0)$,偶数连边$(i,T,b[i],0)$
2,两层之间能配对的点由奇向偶连边$(i,j,inf,c[i]\times c[j])$
$千钧一发$
难点仍然在于构建分层图
我们发现偶数之间满足第二个条件,奇数之间满足第一个条件
这里证明一下两个奇数的平方和不可能是平方数
$\forall a,b(a,b为奇数)$
设$a^{2}+b^{2}=T^{2}$
因为$a^{2}+b^{2}$为偶数,所以$T^{2}$为偶数,所以T为偶数
设$a=2n+1,b=2m+1,T=2p$
$$a^{2}+b^{2}=4p^{2}$$
$$(2n+1)^2+(2m+1)^2=4p^{2}$$
$$4n^{2}+4n+1+4m^{2}+4m+1=4p{2}$$
$$4(n^{2}+n+m^{2}+m)+2=4p^{2}$$
$$n^{2}+n+m^{2}+m+\frac{1}{2}=p^{2}$$
$n^{2}+n+m^{2}+m+\frac{1}{2}=p^{2}$肯定是不成立的
那么我们直接按照奇偶分层,剩下的i就和上一题一样了
$无限之环$
咕咕咕
IV 上下界网络流
就是网络流中有的边不只有上界还有下界
无源汇可行流:
1,建立源汇$ss,tt$
2,原图中的边 $(u,v,[l,r])$ 变成 $(u,v,r-l)$
3,统计$in[i]$代表入边的下界和,$out[i]$代表出边下界和
4,若 $in[i]>out[i]$, 连边$ (ss,i,in[i]-out[i])$,否则建边 $(i,tt,out[i]-in[i])$
跑最大流, 若满流, 则得到一组可行解, 否则无解
其中每条边在原图中流量为下界+反向边流量
有源汇可行流:
在无源汇基础上新建$(t,s,inf)$就好了
得到的可行流为$(t,s,inf)$反向边的流量
有源汇最大流:
拆掉$ss$和$tt$的所有边和$(t,s,inf)$,跑$s->t$最大流
答案为可行流+最大流
有源汇最小流:
拆掉$ss$和$tt$的所有边和$(t,s,inf)$,跑$t->s$最大流
答案为可行流-最大流
有源汇费用流:
基础答案加上下界$\times$ 费用,其他一样
$矩阵$
首先我们发现这题的答案满足单调性
考虑二分,现在的问题是能否满足当前二分的答案mid
现在的要求是每行每列的总和不能>mid或<-mid
考虑如下建图
1,每行向每列连下界为L上界为R的边
2,起点向每行连下界为$(\sum \limits_{j=1}^{m}a[i][j])-mid$,上界为$(\sum\limits_{j=1}^{m}a[i][j])+mid$的边
3,每列向终点连下界为$(\sum\limits_{i=1}^{n}a[i][j])-mid$,上界为$(\sum\limits_{i=1}^{n}a[i][j])+mid$的边

