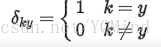softmax VS softmax-loss:数值稳定性

参考：http://freemind.pluskid.org/machine-learning/softmax-vs-softmax-loss-numerical-stability/

The softmax loss layer computes the multinomial logistic loss of the softmax of its inputs. It’s conceptually identical to a softmax layer followed by a multinomial logistic loss layer, but provides a more numerically stable gradient.

中心思想是：在数值计算（或者任何其他工程领域）里，知道一个东西的基本算法和写出一个能在实际中工作得很好的程序之间还是有一段不小的距离的。有很多可能看似无关紧要的小细节小 trick，可能会对结果带来很大的不同。

当然这样的现象其实也很合理：因为理论上的工作之所以漂亮正是因为抓住了事物的主要矛盾，忽略“无关”的细节进行了简化和抽象，从而对比较“干净”的对象进行操作，在一系列的“assumption”下建立起理论体系。但是当要将理论应用到实践中的时候，又得将这些之前被忽略掉了的细节全部加回去，得到一团乱糟糟，在一系列的“assumption”都不再严格满足的条件下找出会出现哪些问题并通过一些所谓的“engineering trick”来让原来的理论能“大致地”继续有效。

softmax函数：

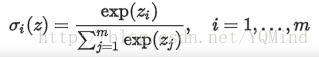
假设$z_i = w_i^Tx+b_i$是第i个类别的线性预测的结果，带入softmax函数的结果是将每一个$z_i$取exponential变成非负，然后除以所有项之和进行归一化。

Multinomial Logistic Loss:

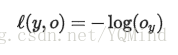
softmax-loss(将softmax和Multinomial Logistic Loss两者结合在一起):
最小化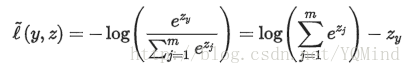，意味着让正确的类别的概率越接近1越好。

在设计 Deep Neural Networks 的库，则可能会倾向于将两者分开来看待，提供两个不同的 Layer 结构比只提供一个合在一起的 Softmax-Loss Layer 要灵活许多，从代码的角度来说也显得更加模块化。但是这里自然地就出现了一个问题：numerical stability。

反向传播说白了就是链式法则Chain Rule，因为 back propagation 是用 chain rule 将导数乘到一起，粗略地讲，如果每一层的导数都“小于一”的话，在层数较多的情况下很容易到后面乘着乘着就接近零了。反过来如果每一层的导数都“大于一”的话，gradient 乘到最后又会出现 blow up 的问题。

说清楚back propagation后，继续看softmax-loss层

同样，如果是softmax层和multinomial logistic loss层，
首先对loss层求导：

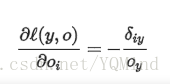
然后到达softmax层，层内导数

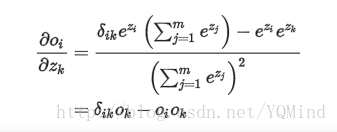
使用链式法则

最终得到和上面一样的结果。但是可以看出，如果分成两层计算的话，要多算好多步骤，除了计算量增大了一点，我们更关心的是数值上的稳定性。由于浮点数是有精度限制的，每多一次运算就会多累积一定的误差。分成两步计算的时候我们需要计算 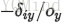，如果碰巧这次预测非常不准，分母接近0，也就是正确的类别所得到的概率非常小（接近零）的话，这里会有溢出的危险。

通过下图，我们可以有一个直观的认识：图中横坐标是 $z_y$大小，纵坐标是分别用两种方法计算出来的结果和“真实值”之间的差距大小。

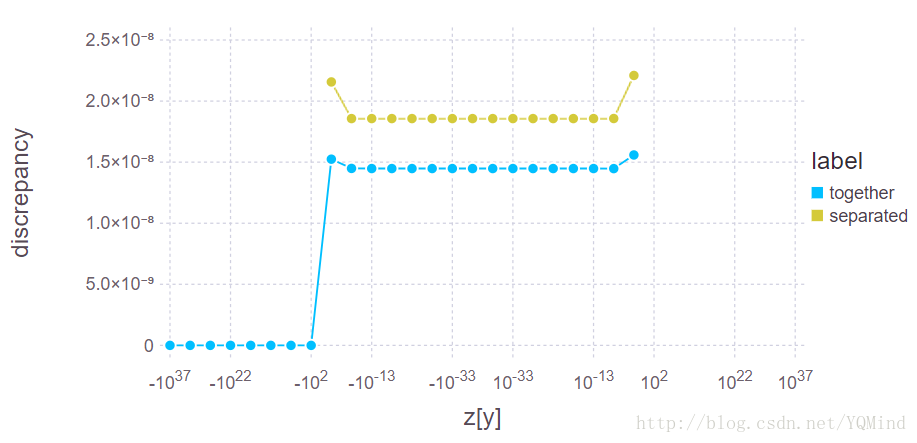
首先可以看到的是单层直接计算确实比分成两层算要好一点，不过从纵坐标上也可以看到两者差距其实非常小。往左边看的话，会发现黄色的点没有了，那是因为结果得到了Nan，$o_y$由于求一个绝对值非常大的负数的 exponential，导致下溢超出 float 可以表示的小数点精度范围，直接变成 0 了，此时$1/o_y$就是Inf，当进行chain rule时，Inf×其他数值，就会直接得到Nan(not a number)。反过来看蓝线的话，好像有点奇怪的是越往左边好像反而变得更加精确了，其实是因为我们的“真实值”也 下溢了，因为 double 虽然比 float 精度高很多，但是也是有限制的。
比较有趣的是往右边的正数半轴看，发现到了 $10^2$之后蓝线和黄线都没有了，说明他们都得到了 NaN，不过这里是另一个问题：对一个比较大的数求 exponential 非常容易发生 overflow。

下面都是指使用softmax-loss:
面对上溢的问题，解决方案：就是在求 exponential 之前将$z$ 的每一个元素减去$z_i$ 的最大值。这样求 exponential 的时候会碰到的最大的数就是 0 了，不会发生 overflow 的问题。但是如果其他数原本是正常范围，现在全部被减去了一个非常大的数，于是都变成了绝对值非常大的负数，所以全部都会发生 underflow，但是 underflow 的时候得到的是 0，这其实是非常 meaningful 的近似值，而且后续的计算也不会出现奇怪的Nan。

当然，总不能在计算的时候平白无故地减去一个什么数，但是在这个情况里是可以这么做的，因为最后的结果要做 normalization，很容易可以证明，这里对$z$ 的所有元素同时减去一个任意数都是不会改变最终结果的——当然这只是形式上，或者说“数学上”，但是数值上我们已经看到了，会有很大的差别。