VINS-MONO ProjectionFactor代码分析及公式推导

ProjectionFactor继承自Ceres的SizedCostFunction。它表示的是第i帧中单位相机平面上的点pts_i重投影到第j帧单位相机平面上的点与匹配点pts_j的投影误差。需要实现构造函数以及重载Evaluate函数。

class ProjectionFactor : public ceres::SizedCostFunction<2, 7, 7, 7, 1>
{
  public:
    EIGEN_MAKE_ALIGNED_OPERATOR_NEW
    ProjectionFactor(const Eigen::Vector3d &_pts_i, const Eigen::Vector3d &_pts_j);
    virtual bool Evaluate(double const *const *parameters, double *residuals, double **jacobians) const;
    void check(double **parameters);

    Eigen::Vector3d pts_i, pts_j;
    Eigen::Matrix<double, 2, 3> tangent_base;
    static Eigen::Matrix2d sqrt_info;
    static double sum_t;
    static int cnt;
};

构造函数及切平面空间的基

ProjectionFactor::ProjectionFactor(const Eigen::Vector3d &_pts_i, const Eigen::Vector3d &_pts_j) : pts_i(_pts_i), pts_j(_pts_j)
{
#ifdef UNIT_SPHERE_ERROR
    Eigen::Vector3d b1, b2;
    Eigen::Vector3d a = pts_j.normalized();
    Eigen::Vector3d tmp(0, 0, 1);
    if(a == tmp)
        tmp << 1, 0, 0;
    b1 = (tmp - a * (a.transpose() * tmp)).normalized();
    b2 = a.cross(b1);
    tangent_base.block<1, 3>(0, 0) = b1.transpose();
    tangent_base.block<1, 3>(1, 0) = b2.transpose();
#endif
};

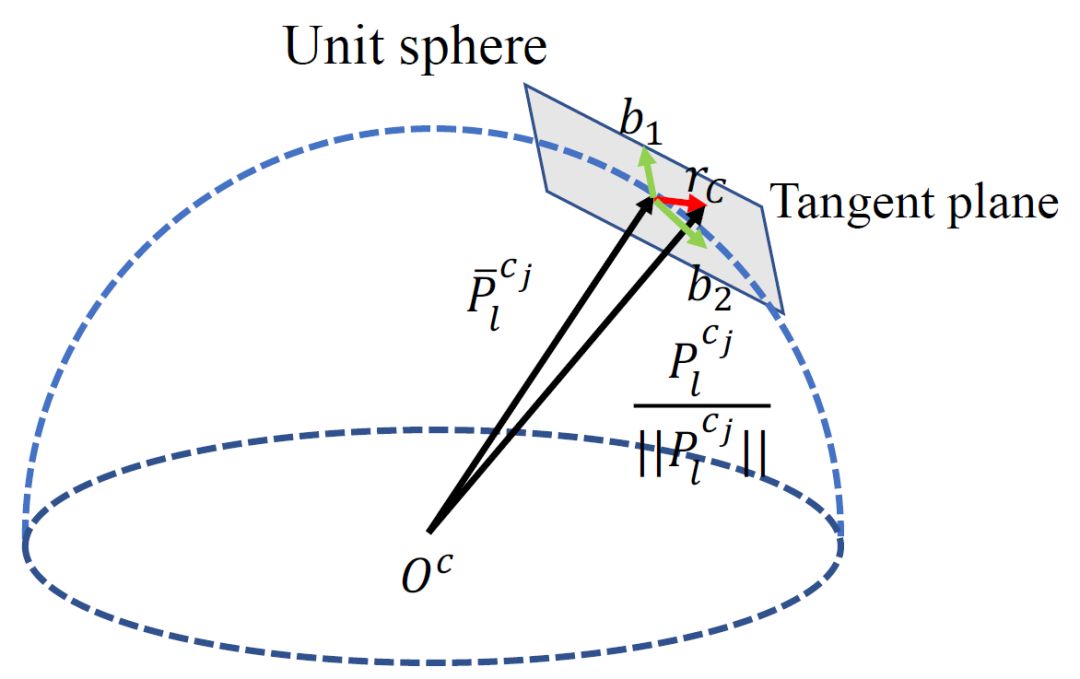
构造函数传入的是重投影误差函数中的常数，也就是一对匹配的特征点。这里是传入的是匹配点在归一化相机平面上的坐标。但重投影误差计算的是单位球面切平面上的误差（为什么要计算球面切平面的误差？而不是直接在单位相机平面的误差？）。这就需要切平面的一组正交基。正交基可以通过施密特正交化来得到。

施密特正交化

施密特正交化是通过一组线性无关的向量生成这组向量所张成空间的一组正交基。引用维基百科的解释：

Gram-Schmidt正交化的基本想法，是利用投影原理在已有正交基的基础上构造一个新的正交基。
设\(\boldsymbol{v} \in \boldsymbol{V^n}\)。\(\boldsymbol{V}^k\)是\(\boldsymbol{V}^n\)上的\(k\)维子空间，其标准正交基为\(\{ \boldsymbol{\eta}_1,\ldots, \boldsymbol{\eta}_k \}\)，且\(\boldsymbol{v}\)不在\(\boldsymbol{V}^k\)上。由投影原理知，\(\boldsymbol{v}\)与其在\(\boldsymbol{V}^k\)上的投影\(\mathrm{proj}_{\boldsymbol{V^k}} \boldsymbol{v}\)之差
\[ \boldsymbol{\beta} = \boldsymbol{v} - \sum_{i=1}^{k}\mathrm{proj}_{\boldsymbol{\eta}_i}\,\boldsymbol{v} = \boldsymbol{v} - \sum_{i=1}^{k}\langle \boldsymbol{v}, \boldsymbol{\eta}_i \rangle \boldsymbol{\eta}_i \]
是正交于子空间\(\boldsymbol{V}^k\)的，亦即\(\boldsymbol{\beta}\)正交于\(\boldsymbol{V}^k\)的正交基\(\boldsymbol{\eta}_i\)。因此只要将\(\boldsymbol{\beta}\)单位化，即
\[ \boldsymbol{\eta}_{k+1} = \frac{\boldsymbol{\beta}}{\|\boldsymbol{\beta}\|} = \frac{\boldsymbol{\beta}}{\sqrt{\langle \boldsymbol{\beta},\boldsymbol{\beta} \rangle }} \]
那么\(\{ \boldsymbol{\eta}_1,\ldots, \boldsymbol{\eta}_{k}, \boldsymbol{\eta}_{k+1} \}\)就是\(\boldsymbol{V}^k\)在\(\boldsymbol{v}\)上扩展的子空间\(\mathrm{span}\{\boldsymbol{v},\boldsymbol{\eta}_1,...,\boldsymbol{\eta}_k\}\)的标准正交基。
根据上述分析，对于向量组\(\{ \boldsymbol{v}_1,\ldots, \boldsymbol{v}_{m} \}\)张成的空间\(\boldsymbol{V}^m\) (\(m<n\))，只要从其中一个向量（不妨设为$ \boldsymbol{v}_1 \(）所张成的一维子空间\) \mathrm{span}{\boldsymbol{v}_1} \(开始（注意到\) \boldsymbol{v}_1 \(就是\) \mathrm{span}{\boldsymbol{v}_1} \(的正交基），重复上述扩展构造正交基的过程，就能够得到\)\boldsymbol{V}^n$ 的一组正交基。这就是'''Gram-Schmidt正交化'''。

算法

首先需要确定已有基底向量的顺序，不妨设为\(\{ \boldsymbol{v}_1,\ldots, \boldsymbol{v}_{n} \}\)。Gram-Schmidt正交化的过程如下：
\[ \begin{split} \boldsymbol{\beta}_1& = &\boldsymbol{v}_1 , & \boldsymbol{\eta}_1 & = & {\boldsymbol{\beta}_1 \over \|\boldsymbol{\beta}_1\|} \\ \boldsymbol{\beta}_2 & = & \boldsymbol{v}_2-\langle \boldsymbol{v}_2 , \boldsymbol{\eta}_1 \rangle \boldsymbol{\eta}_1 , &\boldsymbol{\eta}_2 & =& {\boldsymbol{\beta}_2 \over \|\boldsymbol{\beta}_2\|}\\ \boldsymbol{\beta}_3 & = & \boldsymbol{v}_3 - \langle \boldsymbol{v}_3, \boldsymbol{\eta}_1 \rangle \boldsymbol{\eta}_1 - \langle \boldsymbol{v}_3, \boldsymbol{\eta}_2 \rangle \boldsymbol{\eta}_2 , \qquad & \boldsymbol{\eta}_3 &= & {\boldsymbol{\beta}_3 \over \| \boldsymbol{\beta}_3 \|}\\ \vdots& & & & &\vdots \\ \boldsymbol{\beta}_n & = &\boldsymbol{v}_n-\sum_{i=1}^{n-1}\langle \boldsymbol{v}_n, \boldsymbol{\eta}_i \rangle \boldsymbol{\eta}_i , & \boldsymbol{\eta}_n &= &{\boldsymbol{\beta}_n\over\|\boldsymbol{\beta}_n\|} \end{split}\]
这样就得到\(\mathrm{span}\{ \boldsymbol{v}_1, \ldots , \boldsymbol{v}_n \}\)上的一组正交基\(\{ \boldsymbol{\beta}_1, \ldots , \boldsymbol{\beta}_n \}\)，以及相应的标准正交基\(\{ \boldsymbol{\eta}_1, \ldots , \boldsymbol{\eta}_n \}\)。

施密特正交化的过程中，选择了这组向量中的任意一个\(x_i\)作为一个正交基。那么\(x_i\)和生成的其它正交基\(b_1, \cdots , b_n\)是正交的，它也就正交于\(b_1, \cdots , b_n\)所张成的子空间。

构造函数

构造函数中的代码是通过施密特正交化，求得单位球面在pts_j位置上的切平面子空间的一组正交基。思路是用向量pts_j和\([0,0,1]^T\)找到三维空间的一组标准正交基：\(a = \frac{pts_j}{||pts_j||}, b_1, b_2\)。因为\(b_1,b_2\)与pts_j正交，因此他是单位球面在pts_j处切平面的正交基。
代码中a * (a.transpose() * tmp)的数学公式的表达是\(\frac{<tmp,a>}{<a,a>}a\)，其中\(<x,y>\)表示的是\(x\)和\(y\)的内积。因为\(a\)是单位向量，所以这里的代码中省略了\(<a,a>\)的部分。\(\frac{<tmp,a>}{<a,a>}a\)表示的是\(tmp\)向量在\(a\)向量上的投影，所以\(b_1 = \frac{tmp - \frac{<tmp,a>}{<a,a>}a}{||tmp - \frac{<tmp,a>}{<a,a>}a||}\)垂直与\(a\)向量。\(b_2 = a \times b_1\)同时垂直与\(a\)和\(b_1\),　因此，\(a, b_1, b_2\)构成单位球面所在空间的一组正交基，\(b_1, b_2\)是\(a\)位置上切平面的一组正交基，因为\(a\)与\(b_1, b_2\)正交，所以它也与\(b_1, b_2\)所张成的平面是正交的。

Evaluate函数与残差及雅克比矩阵的推导

先对数学公式的符号表示做一个约定：pts_i表示为\(P_l^{c_i}\)，为第\(l\)个特征点在第i帧单位相机平面的投影；同理pts_j表示为\(P_l^{c_j}\)。pts_i在第\(j\)帧的重投影表示为\({P_l^{c_j}}'\)。第\(i，j\)帧的位姿分别表示为\((R_{b_i}^w,t_{b_i}^w),(R_{b_j}^w, t_{b_j}^w)\)。imu和相机间的外参表示为\((R_c^b, t_c^b)\)。第\(l\)个特征点的逆深度表示为\(\lambda_l\)。切平面基构成的矩阵表示为\(B\)
这样有：
\[{P_l^{c_j}}' = {R_c^b}^T\{{R_{b_j}^w}^T[R_{b_i}^w(R_c^b \frac{P_l^{c_i}}{\lambda_l}+t_c^b)+t_{b_i}^w - t_{b_j}^w] - t_c^b\} \tag{1}\]
残差的公式表示为：
\[\begin{split} e &= &B*(\frac{{P_l^{c_j}}'}{||{P_l^{c_j}}'||_2} - \frac{P_l^{c_j}}{||P_l^{c_j}||_2})\\ &= & B*(\frac{{R_c^b}^T\{{R_{b_j}^w}^T[(R_{b_i}^w(R_c^b \frac{P_l^{c_i}}{\lambda_l}+t_c^b)+t_{b_i}^w - t_{b_j}^w] - t_c^b\}}{||{R_c^b}^T\{{R_{b_j}^w}^T[(R_{b_i}^w(R_c^b \frac{P_l^{c_i}}{\lambda_l}+t_c^b)+t_{b_i}^w - t_{b_j}^w] - t_c^b\}||_2} - \frac{P_l^{c_j}}{||P_l^{c_j}||_2}) \end{split} \tag{2} \]
其中，\(Ｂ, P_l^{c_i},P_l^{c_j}\)是常量，\((R_{b_i}^w,t_{b_i}^w),(R_{b_j}^w, t_{b_j}^w)，(R_c^b, t_c^b),\lambda_l\)是待优化的变量。
需要注意的是，这里的残差是单位球面上残差在切平面上的投影

    Eigen::Vector3d pts_camera_i = pts_i / inv_dep_i;
    Eigen::Vector3d pts_imu_i = qic * pts_camera_i + tic;
    Eigen::Vector3d pts_w = Qi * pts_imu_i + Pi;
    Eigen::Vector3d pts_imu_j = Qj.inverse() * (pts_w - Pj);
    Eigen::Vector3d pts_camera_j = qic.inverse() * (pts_imu_j - tic);
    Eigen::Map<Eigen::Vector2d> residual(residuals);
    residual =  tangent_base * (pts_camera_j.normalized() - pts_j.normalized());

雅克比矩阵的推导

令\(T\)表示待优化的变量，令\(r\)表示投影前的残差，即\(r=\frac{{P_l^{c_j}}'}{||{P_l^{c_j}}'||_2} - \frac{P_l^{c_j}}{||P_l^{c_j}||_2}\)。\(e\)表示残差，则有\(e = B r\)。运用链式法则，可得：
\[{\partial e \over \partial T} = {\partial e\over \partial r}{\partial r \over \partial \frac{{P_l^{c_j}}'}{||{P_l^{c_j}}'||_2}}{\partial \frac{{P_l^{c_j}}'}{||{P_l^{c_j}}'||_2} \over \partial T} = B{\partial \frac{{P_l^{c_j}}^{'}}{||{P_l^{c_j}}^{'}||_2} \over \partial T}\]

残差的雅克比，等于\(\frac{{P_l^{c_j}}'}{||{P_l^{c_j}}'||_2}\)的雅克比在切平面的投影，也就是\(B\)乘以\(\frac{{P_l^{c_j}}'}{||{P_l^{c_j}}'||_2}\)的雅克比。因此先求\(\frac{{P_l^{c_j}}'}{||{P_l^{c_j}}'||_2}\)的雅克比。

对于形如\(\frac{d\frac{f(x)}{||f(x)||_2}}{dx}\)的导数，用链式法则展开，可以得到：
\[\begin{split} \frac{d\frac{f(x)}{||f(x)||_2}}{dx} & = & \frac{df(x)}{dx}\frac{1}{||f(x)||_2} + f(x)\frac{d\frac{1}{||f(x)||_2}}{dx} \\ & = & \frac{df(x)}{dx}\frac{1}{||f(x)||_2} - f(x)\frac{1}{||f(x)||_2^2}\frac{d||f(x)||_2}{dx} \end{split} \tag{3} \]
再来看一下\(\frac{d||f(x)||_2}{dx}\)：
\[\begin{split} \frac{d||f(x)||_2}{dx} & = & \frac{d[f(x)^Tf(x)]^\frac{1}{2}}{dx} \\ & = & \frac{1}{2}[f(x)^Tf(x)]^{-\frac{1}{2}}\frac{d[f(x)^Tf(x)]}{dx} \end{split} \tag{4}\]
要求得\(\frac{d[f(x)^Tf(x)]}{dx}\)，先固定前半部分得到\(f(x)^T\frac{f(x)}{dx}\)。接下来求解前半部分\(f(x)^T\)的导数，因为\(f(x)^Tf(x)\)是标量，所以\(f(x)^Tf(x) = [f(x)^Tf(x)]^T = f(x)^T[f(x)^T]^T\)，仍然固定前半部分得到\(f(x)^T\frac{d[f(x)^T]^T}{dx} = f(x)^T\frac{df(x)}{dx}\)。所以有：
\[\frac{d||f(x)||_2}{dx} = 2f(x)^T\frac{df(x)}{dx} \tag{5}\]

将公式\((5)\)，代入公式\((4)\)、\((3)\)，并将\(\frac{df(x)}{dx}\)记作\(f^{'}(x)\)，得到：
\[\begin{split} \frac{d\frac{f(x)}{||f(x)||_2}}{dx} & = & \frac{1}{||f(x)||_2}f^{'}(x) - \frac{1}{||f(x)||_2^3}f(x)f(x)^Tf^{'}(x) \\ & = & (\frac{1}{||f(x)||_2} - \frac{1}{||f(x)||_2^3}f(x)f(x)^T)f^{'}(x) \end{split} \tag{6}\]

公式\((6)\)中的\(\frac{1}{||f(x)||_2} - \frac{1}{||f(x)||_2^3}f(x)f(x)^T\)就是代码中的\(norm\_jaco\)，其中\(f(x) = {P_l^{c_j}}'\)就是代码中的\(pts\_camera\_j\)。\(reduce = B * norm\_jaco\)。

double norm = pts_camera_j.norm();
Eigen::Matrix3d norm_jaco;
double x1, x2, x3;
x1 = pts_camera_j(0);
x2 = pts_camera_j(1);
x3 = pts_camera_j(2);
norm_jaco << 1.0 / norm - x1 * x1 / pow(norm, 3), - x1 * x2 / pow(norm, 3),            - x1 * x3 / pow(norm, 3),
             - x1 * x2 / pow(norm, 3),            1.0 / norm - x2 * x2 / pow(norm, 3), - x2 * x3 / pow(norm, 3),
             - x1 * x3 / pow(norm, 3),            - x2 * x3 / pow(norm, 3),            1.0 / norm - x3 * x3 / pow(norm, 3);
reduce = tangent_base * norm_jaco;

有了\(reduce\)之后，只需要求出\(pts\_camera\_j\)的雅克比，然后将它们相乘，就可以求出残差函数的雅克比矩阵。

\(pts\_camera\_j\)的雅克比矩阵

将公式\((1)\)展开，可以得到
\[ {P_l^{c_j}}' = {R_c^b}^T{R_{b_j}^w}^T R_{b_i}^w R_c^b P_l^{c_i}\frac{1}{\lambda_l} + {R_c^b}^T{R_{b_j}^w}^T R_{b_i}^w t_c^b + {R_c^b}^T{R_{b_j}^w}^T t_{b_i}^w - {R_c^b}^T{R_{b_j}^w}^T t_{b_j}^w - {R_c^b}^T t_c^b\]
我们需要分别求解\({P_l^{c_j}}'\)关于\((R_{b_i}^w,t_{b_i}^w),(R_{b_j}^w, t_{b_j}^w)，(R_c^b, t_c^b),\lambda_l\)的导数。

关于\((R_{b_i}^w,t_{b_i}^w)\)的导数

可以看到\({P_l^{c_j}}'\)中仅有前三项与第\(i\)帧的位姿有关。将$ {R_c^b}^T{R_{b_j}^w}^T\(记作\)A\(，将\) R_c^b P_l^{c_i}\frac{1}{\lambda_l} + t_c^b\(记作\)x\(，则\){R_c^b}^T{R_{b_j}^w}^T R_{b_i}^w R_c^b P_l^{c_i}\frac{1}{\lambda_l} + {R_c^b}^T{R_{b_j}^w}^T R_{b_i}^w t_c^b + {R_c^b}^T{R_{b_j}^w}^T t_{b_i}^w = A(R_{b_i}^w x + t_{b_i}^w)$

在SE(3)上的推导

令\(\xi = [\rho, \phi]^T, \rho = J^{-1}t\)，根据\(SE(3)\)在李代数上的求导公式视觉SLAM十四讲
\[{\partial Tp \over \partial \xi} = \begin{bmatrix} I & -(Rp+t)^{\land} \\ 0^T & 0^T\end{bmatrix}\]
因为\(\rho = J^{-1}t\)，所以：
\[{\partial [\rho ,\phi]^T \over \partial[t, \phi]^T} = \begin{bmatrix} J^{-1} & 0 \\ 0 & I\end{bmatrix}\]
所以：
\[{\partial Tp \over \partial [t, \phi]^T} = {\partial Tp \over \partial [\rho, \phi]^T}{\partial[\rho, \phi]^T \over \partial [t, \phi]^T} = \begin{bmatrix} J^{-1} & -(Rp+t)^{\land} \\ 0^T & 0^T \end{bmatrix}\]
所以：
\[{\partial {P_l^{c_j}}' \over \partial [t, \phi]^T} = [AJ^{-1} \quad -A(Rp+t)^{\land}]\]
这种推导方式需要求\(J^{-1}\)，计算比较复杂。还可以用一种简单的推导方式。

扰动模型推导

分别对\(t\)和\(R\)求导。
对\(t_{b_i}^w\)求导非常简单，\({\partial {P_l^{c_j}}'\over {\partial t_{b_i}^w}} = A = {R_c^b}^T{R_{b_j}^w}^T\)
对于\(R\)的求导的扰动模型有左扰动模型和右扰动模型。如果\((R,T)\)是将点从世界坐标系转到body坐标系，则用左扰动模型，反之，则用右扰动模型。这里显然用右扰动。

左扰动模型

\[ \begin{split} {\partial {P_l^{c_j}}'\over {\partial \delta \phi}} & = &\lim_{\delta \phi \to 0}{ [A \exp(\delta\phi^{\land}) \exp(\phi_i^{\land}) x +At_{b_i}^w ]- [A\exp(\phi_i^{\land}) x +At_{b_i}^w]\over \delta \phi } \\ & = &\lim_{\delta \phi \to 0} { A[\exp(\delta\phi^{\land}) - I] \exp(\phi_i^{\land})x \over \delta \phi}\\ &=& \lim_{\delta \phi \to 0} { A(I+\delta \phi^{\land} - I)\exp(\phi_i^{\land})x \over \delta \phi} \\ &=& \lim_{\delta \phi \to 0} {-A[\exp(\phi_i^{\land})x]^\land \delta \phi\over \delta \phi} \\ & = & -{R_c^b}^T{R_{b_j}^w}^T[R_{b_i}^w(R_c^b P_l^{c_i}\frac{1}{\lambda_l}+t_c^b)]^{\land} \end{split}\]

右扰动模型

\[ \begin{split} {\partial {P_l^{c_j}}'\over {\partial \delta \phi}} & = &\lim_{\delta \phi \to 0}{ [A \exp(\phi_i^{\land}) \exp(\delta\phi^{\land})x +At_{b_i}^w ]- [A\exp(\phi_i^{\land}) x +At_{b_i}^w]\over \delta \phi } \\ & = &\lim_{\delta \phi \to 0} { A\exp(\phi_i^{\land})[\exp(\delta\phi^{\land}) - I] x \over \delta \phi}\\ &=& \lim_{\delta \phi \to 0} { A\exp(\phi_i^{\land}) (I+\delta \phi^{\land} - I)x \over \delta \phi} \\ &=& \lim_{\delta \phi \to 0} {-A\exp(\phi_i^{\land})x^\land \delta \phi\over \delta \phi} \\ & = & -{R_c^b}^T{R_{b_j}^w}^TR_{b_i}^w(R_c^b P_l^{c_i}\frac{1}{\lambda_l}+t_c^b)^{\land} \end{split}\]

扰动模型的求导都是关于扰动的求导。
在迭代优化的方法中，我们需要找到残差函数关于状态量的雅克比矩阵，但是扰动模型的求导都是关于扰动的求导，为什么它可以代替关于状态量的雅克比呢？这需看一下扰动量\(\Delta x\)与雅克比的关系。
以高斯－牛顿法举例。
我们不停地在找\(\Delta x^* = \arg \min \limits_{\Delta x}||f(x+\Delta x)||^2\)。高斯－牛顿法是把\(f(x+\Delta x)\)做一阶泰勒展开。\(f(x+\Delta x) \approx f(x)+J(x)\Delta x\)。这个时候就需要找\(\Delta x^* = \arg \min \limits_{\Delta x}||f(x)+J(x)\Delta x)||^2\)。将里面的二次项展开可以得到：
\[\begin{split} ||f(x)+J(x)\Delta x)||^2 &=& [f(x)+J(x)\Delta x]^T[f(x) + J(x)\Delta x] \\ &=&||f(x)||^2 + 2f(x)^TJ(x)\Delta x + \Delta x^TJ(x)^TJ(x)\Delta x \end{split}\]
将上式关于\(\Delta x\)求导，并令导数等于０，就可以求得是\(||f(x+\Delta x)||^2\)最小的\(\Delta x^*\)。
\[J(x)^Tf(x) + J(x)^TJ(x)\Delta x = 0\]
所以，雅克比\(J\)和\(\Delta x\)之间的关系是它们要能够表达出\(f(x+\Delta x)\)的一阶近似。对于有加法运算的欧式变量来说，雅克比\(J = J(x)\)，没有问题。但是对于位姿等一些没有加法的变量来说，它就不成立了。引用知乎上的一篇解释《Computing Jacobian, why error state?》：

从严谨的角度来说，我们应当对误差求Jacobian，这样才能满足部分不符合狭义加法定义的状态之需求。
下面来详细的聊一聊为什么（其实并没有多长）:
首先，在Gauss-Newton法中，我们渴望得到一个cost function的下述的线性展开：
\[f(x_0 \oplus dx) = f(x_0)+Jdx\]
其中\(\oplus\) 表示广义加法。
那么我们来看看如果利用关于状态\(x=x_0\)处的Jacobian来做泰勒展开，\(f(x_0 \oplus dx)\) 会变成什么样：
\[f(x_0 \oplus dx) = f(x_0)+f^{\prime}(x_0)(x_0 \oplus dx - x_0)\]
注意 \((x_0)(x_0 \oplus dx - x_0)\)这一项，当状态\(x\)是位置、速度这种欧式量的时候，ok没问题，\(\oplus\)退化为狭义加法\(+\)，这个项就等于\(dx\) 。
但当状态\(x\)是姿态等其他流形的时候，上述性质就不存在了，这个泰勒展开将不会是我们想要的形式。此时我们应当将\(f(x_0+dx)\)看作一个关于\(dx\)的函数\(F(dx)\) （扰动模型），将它在\(dx=0\)处做泰勒展开：
\[\begin{split} f(x_0+dx) & = & F(dx) \\ & = & F(0) + F^{\prime}(0)(dx-0) \\ & = & f(x_0 \oplus 0) + F^{\prime}(0)dx \\ & = & f(x_0) + {\partial f(x_0 \oplus dx) \over \partial dx}dx \end{split}\]
其中那一坨分式表示的就是原始cost function关于\(dx=0\)的Jacobian。我们可以发现，这个泰勒展开满足我们所想要的第一个公式中的形式了！
此外，当状态\(x\)是欧式量时，无论是对状态本身（在\(x=x_0\)处）求Jacobian，还是对误差状态（在\(dx=0\)处）求Jacobian，都可以得到相同的渴望的线性形式（可以自己推推看）。所以，为了符号的统一，我们就直接写关于误差状态的Jacobian好了。
当然，有的作者写paper时不会那么严谨，可能符号直接也写成对状态求Jacobian的样子了。看到的时候不要过于纠结，心中有数就行。

高翔对这个问题的解释：

按照定义，左乘一个扰动，然后令扰动趋于零，求目标函数相对于扰动的变化率，作为导数来使用。
同时，在优化过程中，用这种导数算出来的增量，以左乘形式更新在当前估计上，于是使估计值一直在SO(3)或SE(3)上。这种手段称为“流形上的优化”。

另一个解释：

在图优化里，Jacobian 最终就应该是 w.r.t. ( with respect to)增量的；因为求解Gauss-Newton系统 ( H dx = b) 时，待解量是增量。
优化问题是干什么呢？是为了找一个增量，这个增量使代价函数变小，也就是使 e(x) 变小。e(x) 对 dx 的Jacobian 又是什么呢？是 e(x) 随 dx 增加的变化率。让 dx 一直朝向使 e(x) 小的方向走，这就是图优化迭代的过程。所以说，Jacobian 最终就应该是 w.r.t. 增量的。

代码对应的是右扰动模型。

if (jacobians[0])
{
    Eigen::Map<Eigen::Matrix<double, 2, 7, Eigen::RowMajor>> jacobian_pose_i(jacobians[0]);
    Eigen::Matrix<double, 3, 6> jaco_i;
    jaco_i.leftCols<3>() = Ric_m_Rj;
    jaco_i.rightCols<3>() = Ric_m_Rj_m_Ri * -spec_skewSymmetric(pts_imu_i);
    jacobian_pose_i.leftCols<6>() = reduce * jaco_i;
    jacobian_pose_i.rightCols<1>().setZero();
}

最后一个问题，函数中的参数都是四元数，但这里使用的扰动模型，是关于扰动的李代数的求导。使用这个雅克比可以得到\(q\)的梯度下降的方向的扰动吗？
这个问题其实涉及到Cerese solver关于过参数化的处理机制。当过参数化的时候，为了计算效率等原因，优化的过程其实是在参数的切空间上进行的。例如参数是四元数或者旋转矩阵，优化过程是在李代数上进行的。这个时候需要继承LocalParameterization类，实现一个泛化的加法运算以及一个参数关于切空间参数的的雅克比矩阵。优化的过程当中，Ceres会把CostFunction中的雅克比和LocalParameterization中的雅克比相乘，作为计算\(J^TJ \Delta x = -J^Tf(x)\)中的\(J\)。得到的\(\Delta x\)通过泛化的加法跟新CostFunction中的参数。引用Ceres官方文档的解释：

 class LocalParameterization {
 public:
  virtual ~LocalParameterization() {}
  virtual bool Plus(const double* x,
                    const double* delta,
                    double* x_plus_delta) const = 0;
  virtual bool ComputeJacobian(const double* x, double* jacobian) const = 0;
  virtual bool MultiplyByJacobian(const double* x,
                                  const int num_rows,
                                  const double* global_matrix,
                                  double* local_matrix) const;
  virtual int GlobalSize() const = 0;
  virtual int LocalSize() const = 0;
};

Sometimes the parameters \(x\) can overparameterize a problem. In that case it is desirable to choose a parameterization to remove the null directions of the cost. More generally, if \(x\) lies on a manifold of a smaller dimension than the ambient space that it is embedded in, then it is numerically and computationally more effective to optimize it using a parameterization that lives in the tangent space of that manifold at each point.

For example, a sphere in three dimensions is a two dimensional manifold, embedded in a three dimensional space. At each point on the sphere, the plane tangent to it defines a two dimensional tangent space. For a cost function defined on this sphere, given a point \(x\), moving in the direction normal to the sphere at that point is not useful. Thus a better way to parameterize a point on a sphere is to optimize over two dimensional vector \(\Delta x\) in the tangent space at the point on the sphere point and then “move” to the point \(x+\Delta x\), where the move operation involves projecting back onto the sphere. Doing so removes a redundant dimension from the optimization, making it numerically more robust and efficient.

More generally we can define a function
\[x' = \boxplus(x, \Delta x)\]
where \(x′\) has the same size as \(x\), and \(\Delta x\) is of size less than or equal to \(x\). The function \(\boxplus\), generalizes the definition of vector addition. Thus it satisfies the identity
\[\boxplus(x,0)=x, \forall x\]
Instances of LocalParameterization implement the \(\boxplus\) operation and its derivative with respect to \(\Delta x\) at \(\Delta x=0\).

到这里还不能解释为什么CostFunction中的雅克比是关于扰动的雅克比再加上一个全零的列。这个其实是实现上的一个trick。前面说过优化中需要计算两个雅克比的乘积来作为最终的雅克比矩阵。这个比较低效。既然我们最终需要的是关于扰动的雅克比一个trick是在CostFunction的雅克比中，它的左上角设置为关于扰动的雅克比，其它部分为\(0\)。LocalParameterization中的雅克比左上角设置为单位矩阵\(I\)，其它部分为\(0\)。这样两者的乘积就是关于扰动的雅克比。写成公式：
\[\begin{bmatrix} {\partial e \over \partial \alpha}\lvert_{2\times 6} \quad 0\lvert_{2\times 1}\end{bmatrix}_{2\times 7} \begin{bmatrix} I\lvert_{6 \times 6} \\ 0\lvert_{1\times 6}\end{bmatrix}_{7 \times 6} = \begin{bmatrix} {\partial e \over \partial \alpha}\end{bmatrix}_{2 \times 6}\]

可以参考《On-Manifold Optimization Demo using Ceres Solver》

In many on-manifold graph optimization problems, only J_err_alg are required. However, in Ceres Solver, one can only seperately assign J_err_grp and J_grp_alg, but cannot directly define J_err_alg. This may be redundant and cost extra computational resources:
One has to derive the explicit Jacobians equations of both J_err_grp and J_grp_alg.
The solver would spend extra time to compute J_err_alg by multiplying J_err_grp and J_grp_alg.
Therefore, for convenience, we use a not-that-elegant but effective trick. Let’s say that the error function term is of dimension m, the Lie group N, and the Lie algebra n. We define the leading mn block in J_err_grp to be the actual J_err_alg, with other elements to be zero; and define the leading nn block in J_grp_alg to be identity matrix, with other elements to be zero. Thus, we are free of deriving the two extra Jacobians, and the computational burden of the solver is reduced – although Ceres still has to multiply the two Jacobians, the overall computational process gets simpler.

class PoseLocalParameterization : public ceres::LocalParameterization
{
public:
    EIGEN_MAKE_ALIGNED_OPERATOR_NEW
private:
    virtual bool Plus(const double *x, const double *delta, double *x_plus_delta) const;
    virtual bool ComputeJacobian(const double *x, double *jacobian) const;
    virtual int GlobalSize() const { return 7; };
    virtual int LocalSize() const { return 6; };
};
bool PoseLocalParameterization::Plus(const double *x, const double *delta, double *x_plus_delta) const
{
    Eigen::Map<const Eigen::Vector3d> _p(x);
    Eigen::Map<const Eigen::Quaterniond> _q(x + 3);

    Eigen::Map<const Eigen::Vector3d> dp(delta);

    Eigen::Quaterniond dq = Utility::deltaQ(Eigen::Map<const Eigen::Vector3d>(delta + 3));

    Eigen::Map<Eigen::Vector3d> p(x_plus_delta);
    Eigen::Map<Eigen::Quaterniond> q(x_plus_delta + 3);

    p = _p + dp;
    q = (_q * dq).normalized();

    return true;
}
bool PoseLocalParameterization::ComputeJacobian(const double *x, double *jacobian) const
{
    Eigen::Map<Eigen::Matrix<double, 7, 6, Eigen::RowMajor>> j(jacobian);
    j.topRows<6>().setIdentity();
    j.bottomRows<1>().setZero();

    return true;
}

关于\((R_{b_j}^w,t_{b_j}^w)\)的导数

关于\((R_{b_j}^w,t_{b_j}^w)\)的导数与关于\((R_{b_i}^w,t_{b_i}^w)\)的导数，非常类似，但以为\((R_{b_j}^w,t_{b_j}^w)\)用的是转置，所以实质上用的是左扰动模型。我们也可以用形式上的右扰动模型推导一下，但因为转置的存在它实际上还是左扰动。为了书写的方便这里把\(R_{b_i}^w(R_c^b \frac{P_l^{c_i}}{\lambda_l}+t_c^b)\)也就是代码中的pts_w记作\(x\)，则\({P_l^{c_j}}' = {R_c^b}^T{R_{b_j}^w}^T x - {R_c^b}^T{R_{b_j}^w}^T t_{b_j}^w - {R_c^b}^T t_c^b\)。
关于\(t_{b_j}^w\)的导数直接可以得到：
\[{\partial {P_l^{c_j}}' \over \partial t_{b_j}^w} = -{R_c^b}^T {R_{b_j}^w}^T\]
关于\(R_{b_j}^w\)的导数:
\[\begin{split} {\partial {P_l^{c_j}}' \over \partial \Delta \phi} & = & \lim_{\Delta \phi \to 0}{ {R_c^b}^T {[R_{b_j}^w \exp(\Delta \phi ^{\land})]}^T(x - t_{b_j}^w) - {R_c^b}^T {R_{b_j}^w}^T(x - t_{b_j}^w) \over \Delta \phi} \\ & = & \lim_{\Delta \phi \to 0} { {R_c^b}^T[\exp(\Delta \phi^{\land})^T-I] {R_{b_j}^w}^T(x-t_{b_j}^w)\over \Delta \phi} \\ & = & \lim_{\Delta \phi \to 0} { {R_c^b}^T[(I+\Delta \phi^{\land})^T-I] {R_{b_j}^w}^T(x-t_{b_j}^w)\over \Delta \phi} \\ & = & \lim_{\Delta \phi \to 0} { {R_c^b}^T(-\Delta \phi^{\land}) {R_{b_j}^w}^T(x-t_{b_j}^w)\over \Delta \phi} \\ & = & \lim_{\Delta \phi \to 0} { {R_c^b}^T({R_{b_j}^w}^T(x-t_{b_j}^w))^{\land} \Delta \phi\over \Delta \phi} \\ & = & {R_c^b}^T({R_{b_j}^w}^T(x-t_{b_j}^w))^{\land} \\ & = & {R_c^b}^T({R_{b_j}^w}^T(R_{b_i}^w(R_c^b \frac{P_l^{c_i}}{\lambda_l}+t_c^b) -t_{b_j}^w))^{\land} \end{split}\]
其中，\({R_{b_j}^w}^T(R_{b_i}^w(R_c^b \frac{P_l^{c_i}}{\lambda_l}+t_c^b) -t_{b_j}^w)\)就是代码中的pts_imu_j。

            Eigen::Map<Eigen::Matrix<double, 2, 7, Eigen::RowMajor>> jacobian_pose_j(jacobians[1]);

            Eigen::Matrix<double, 3, 6> jaco_j;
            jaco_j.leftCols<3>() = -Ric_m_Rj;//ric_tranpose * - Rj_tranpose;
            jaco_j.rightCols<3>() = ric_tranpose * spec_skewSymmetric(pts_imu_j);

            jacobian_pose_j.leftCols<6>() = reduce * jaco_j;
            jacobian_pose_j.rightCols<1>().setZero();

关于\((R_c^b,t_c^b)\)的导数

既有左扰动又有右扰动，略微复杂。
关于\(t_c^b\)的导数直接可以得到：
\[{\partial {P_l^{c_j}}' \over \partial t_c^b} =(R_c^b)^T{R_{b_j}^w}^T R_{b_i}^w - {R_c^b}^T\]
关于\(R_c^b\)的导数:
这里令\(P_l^{c_i}\frac{1}{\lambda_l} = x\)，令\({R_{b_j}^w}^T R_{b_i}^w = R_i^j\)，重写$ {P_l^{c_j}}'$的公式：
\[ \begin{split} {P_l^{c_j}}' &= &{R_c^b}^T{R_{b_j}^w}^T R_{b_i}^w R_c^b P_l^{c_i}\frac{1}{\lambda_l} + {R_c^b}^T{R_{b_j}^w}^T R_{b_i}^w t_c^b + {R_c^b}^T{R_{b_j}^w}^T t_{b_i}^w - {R_c^b}^T{R_{b_j}^w}^T t_{b_j}^w - {R_c^b}^T t_c^b \\ & = & {R_c^b}^T R_i^j R_c^bx + {R_c^b}^T(R_i^jt_c^b + R_{b_i}^wt_{b_i}^w-R_{b_j}^wt_{b_j}^w-t_c^b) \end{split}\]
再令\(R_i^jt_c^b + R_{b_i}^wt_{b_i}^w-R_{b_j}^wt_{b_j}^w-t_c^b = y\)，则\({P_l^{c_j}}' = {R_c^b}^T R_i^j R_c^bx+ {R_c^b}^T y\)。右扰动求导：
\[\begin{split} { \partial {P_l^{c_j}}'\over \partial \Delta \phi} & = & \lim_{\Delta \phi \to 0}{ {[R_c^b\exp(\Delta \phi^{\land})]}^T R_i^j R_c^b\exp(\Delta \phi^{\land})x - {R_c^b}^T R_i^j R_c^bx\over \Delta \phi} + \lim_{\Delta \phi \to 0}{ {[R_c^b\exp(\Delta \phi^{\land})]}^T y - {R_c^b}^T y \over \Delta \phi} \\ & =& \lim_{\Delta \phi \to 0}{(I-\Delta \phi^{\land}){R_c^b}^T R_i^j R_c^b(I+\Delta \phi^{\land}) x - {R_c^b}^T R_i^j R_c^bx\over \Delta \phi} + \lim_{\Delta \phi \to 0}{(I-\Delta \phi^{\land}){R_c^b}^T y - {R_c^b}^T y\over \Delta \phi}\\ & = & \lim_{\Delta \phi \to 0}{{R_c^b}^T R_i^j R_c^b\Delta \phi^{\land} x - \Delta \phi^{\land}{R_c^b}^T R_i^j R_c^bx - \Delta \phi^{\land}{R_c^b}^T R_i^j R_c^b\Delta \phi^{\land} x\over \Delta \phi}+\lim_{\Delta \phi \to 0}{({R_c^b}^Ty)^{\land }\Delta \phi\over \Delta \phi} \\ & = & \lim_{\Delta \phi \to 0}{-{R_c^b}^T R_i^j R_c^bx^{\land} \Delta \phi + [{R_c^b}^T R_i^j R_c^bx]^{\land}\Delta \phi \over \Delta \phi} + ({R_c^b}^Ty)^{\land } \\ & = & -{R_c^b}^T R_i^j R_c^bx^{\land} + [{R_c^b}^T R_i^j R_c^bx]^{\land} + ({R_c^b}^Ty)^{\land } \\ & = & -{R_c^b}^T {R_{b_j}^w}^T R_{b_i}^w R_c^b(P_l^{c_i}\frac{1}{\lambda_l})^{\land} + [{R_c^b}^T {R_{b_j}^w}^T R_{b_i}^w R_c^b P_l^{c_i}\frac{1}{\lambda_l}]^{\land} + [{R_c^b}^T ({R_{b_j}^w}^T R_{b_i}^w t_c^b + R_{b_i}^wt_{b_i}^w-R_{b_j}^wt_{b_j}^w-t_c^b)]^{\land } \end{split}\]

Eigen::Map<Eigen::Matrix<double, 2, 7, Eigen::RowMajor>> jacobian_ex_pose(jacobians[2]);

Eigen::Matrix<double, 3, 6> jaco_ex;
jaco_ex.leftCols<3>() = Ric_m_Rj_m_Ri - ric_tranpose; //ric_tranpose * (Rj_tranpose * Ri - Eigen::Matrix3d::Identity());
Eigen::Matrix3d tmp_r = Ric_m_Rj_m_Ri * ric;
jaco_ex.rightCols<3>() = -tmp_r * spec_skewSymmetric(pts_camera_i) + 
                        spec_skewSymmetric1(tmp_r * pts_camera_i) + 
                        spec_skewSymmetric2(ric_tranpose * (Rj_tranpose * (Ri * tic + Pi - Pj) - tic));

jacobian_ex_pose.leftCols<6>() = reduce * jaco_ex;
jacobian_ex_pose.rightCols<1>().setZero();

关于\(\lambda_l\)的导数最简单

\[\frac{\partial {P_l^{c_j}}^{'}}{\partial \lambda_l} = \frac{\partial {R_c^b}^T {R_{b_j}^w}^T R_{b_i}^w R_c^b P_l^{c_i}\frac{1}{\lambda_l}}{\partial \lambda_l} = -{R_c^b}^T {R_{b_j}^w}^T R_{b_i}^w R_c^b P_l^{c_i}\frac{1}{\lambda_l^2}\]

代码如下：

jacobian_feature = reduce * ric.transpose() * Rj.transpose() * Ri * ric * pts_i * -1.0 / (inv_dep_i * inv_dep_i);

协方差矩阵

优化中使用的是马氏距离，需要用协方差矩阵\(\Sigma\)来做归一化。因此在残差和雅克比的计算中需要左乘\(\Sigma^{-{1\over 2}}\)。

    residual = sqrt_info * residual;

雅克比部分体现在reduce中：

    reduce = sqrt_info * reduce;

sqrt_info在backend的setParameter中赋值。像素噪声的标准差为\(1.5\)个像素。

    ProjectionFactor::sqrt_info = FOCAL_LENGTH / 1.5 * Matrix2d::Identity();