数学建模--遗传算法（从零开始学）

其他 2019-10-27 10:44:38 阅读次数: 0
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接： https://blog.csdn.net/weixin_41122036/article/details/99621870

学习数学建模常见算法–遗传算法.

首先，确定一下学习路线和学习资料（按照这个路线，入门非常容易，主要是人家文章写得好！）：

  • 视频：https://www.bilibili.com/video/av11893597?from=search&seid=7014684773398800271
      主要讲绪论知识和基本理论以及简单的例程，不涉及编程。
       适合：完全不懂遗传算法的同学可作为先验知识。
  • 课件：链接：https://pan.baidu.com/s/1HER9V64ninS2k0imiEEoKA 提取码：zzp8
      非常通俗的讲解，适合看完视频后再看这个课件，讲解有一定算法思想。有一个实验，但是是使用c语言编写。后边我会用matlab代码进行重写。
  • matlab遗传算法实验：遗传算法解决最优解问题
      这篇文章非常通俗易懂，有前面的基础知识后非常容易看懂，写的也很有意思，看着就是笔者已经将这个算法吃透了。
    我复现了笔者的实验，实验结果很好，这里就不再贴图（实际是做完忘记截图了…）。
    本文例题可以使用蚁群算法解决：蚁群算法
1、根据笔者的实验自己做了上边提到的课件中的题目：关于香蕉函数（Rosenbrock函数）的最大值求解问题。

思路：

  • 1、编码与解码：分别使用十位二进制数表示x1，x2，那么种群中的每个个体就是20位二进制数。（编码方式参见上边提到的课件）
    二进制数转化为十进制数算法：
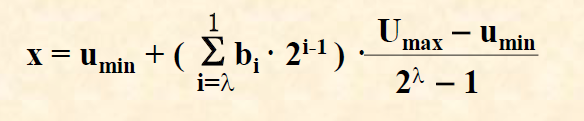
    在这里插入图片描述
    表现在这道题目就是：Umin = -2.048,Umax = 2.048 ，λ = 10，bi是十位二进制中的每一个值（仅有0 、1）；
    所以 x 1 = U m i n + ( ∑ i = λ 1 b i ∗ 2 i − 1 ) U m a x − U m i n 2 λ − 1 x_{1}=Umin + (\sum_{i=\lambda }^{1}b_{i}\ast 2^{i-1})\frac{Umax-Umin}{2^{\lambda } - 1}
    即：
    x 1 = − 2.048 + ( ∑ i = 10 1 b i ∗ 2 i − 1 ) 4.096 2 10 − 1 x_{1}=-2.048 + (\sum_{i=10 }^{1}b_{i}\ast 2^{i-1})\frac{4.096}{2^{10 } - 1}
    x2同理。

  • 2、适应度函数： f(x1, x2)是恒大于0的数，所以可以直接用作适应度函数。

  • 3、比例选择、交换、变异算子：选择复制、交换，变异均使用上面matlab实验的解法。
    matlab代码如下：

    main.m

function main()
clear;
clc;
%种群大小
popsize = 90;
%二进制编码长度
chromelength = 20;
%交叉概率
pc = 0.7;
%变异概率
pm = 0.01;
%初始种群 %pop = population 种群
pop = initpop(popsize, chromelength);
%迭代100次
for i = 1:100
   %计算适应度值?
   objvalue = cal_objvalue(pop);
   fitvalue = objvalue;	
   %选择复制
   newpop = selection(pop, fitvalue);
   %交换
   newpop = crossover(newpop, pc);
   %变异
   newpop = mutation(newpop, pm);
   %更新种群
   pop = newpop;
   %寻找最优解并打印在command窗口
   [bestindividual, bestfit] = best(pop, fitvalue);
   [x1b, x2b] = binary2decimal(bestindividual);
   fprintf('the best x1 is -->>%5.2f\n', x1b);
   fprintf('the best x2 is -->>%5.2f\n', x2b);
   fprintf('the best y is -->>%5.2f\n', bestfit);
   %更新后的种群
   [x1, x2] = binary2decimal(newpop);
   y = cal_objvalue(newpop);
   %每迭代10次就输出一次图像，观察效果
   if mod(i, 10) == 0
   	figure;
   	x3 = -2.048:0.01:2.048;
   	x4 = -2.048:0.01:2.048;
   	[x5, x6] = meshgrid(x3, x4);
   	y1 = (1 - x5).^2 + 100*(x6 - x5.^2).^2;
   	mesh(x5, x6, y1);
   	hold on;
   	plot3(x1, x2, y, '*');
   	title(['iteration is' num2str(i)]);
   end
end

initpop.m(初始化种群函数)

%初始化种群
function pop = initpop(popsize, chromelength)
%随机产生90*20的0 1序列作为初始化种群
pop = round(rand(popsize, chromelength));

binary2decimal.m(二进制转换为十进制函数)

%二进制转化为十进制
function [pop3 pop4] = binary2decimal(pop)

[px, py] = size(pop);
%计算x1的数值矩阵
for i = 1:py - 10
	pop1(:,i) = 2.^(py - 10 - i)*pop(:,i);
end
%计算x2的数值矩阵
for i = 11:py
	pop2(:,i - 10) = 2.^(py - i)*pop(:,i);
end
%x1求和后的列向量
temp1 = sum(pop1, 2);
%x2求和后的列向量 
temp2 = sum(pop2, 2);
%x1转换为十进制
pop3 = -2.048 + 4.096/1023*temp1;
%x2转化为十进制
pop4 = -2.048 + 4.096/1023*temp2;

cal_value.m(计算适应度函数)

%计算适应度函数（也就是香蕉函数值）
function objvalue = cal_objvalue(pop)

[x1, x2] = binary2decimal(pop);
objvalue = (1 - x1).^2 + 100*(x2 - x1.^2).^2;

selection.m(选择复制函数)

%选择和复制  轮盘赌法
function [newpop] = selection(pop, fitvalue)
[px, py] = size(pop);
totalfit = sum(fitvalue);
p_fitvalue = fitvalue/totalfit;
%概率求和排序
p_fitvalue = cumsum(p_fitvalue);
%产生随机概率并排序
ms = sort(rand(px, 1));
fitin = 1;
newin = 1;
while newin <= px
	if(ms(newin) < p_fitvalue(fitin))
		newpop(newin,:) = pop(fitin,:);
		newin = newin + 1;
		
	else
		fitin = fitin + 1;
	end
	
end

crossover.m(交换函数)

%交换
function [newpop] = crossover(pop, pc)
[px, py] = size(pop);
newpop = ones(size(pop));
%理论是随机交换（交换哪个，和谁交换，交换哪一部分都是随机的），这里采用i和i+1的随机部分交换，尽可能达到随机
for i = 1:2:px - 1
	if(rand < pc)
		cpoint = round(rand*py);
		newpop(i,:) = [pop(i,1:cpoint), pop(i+1, cpoint + 1:py)];
		newpop(i+1, :) = [pop(i+1,1:cpoint), pop(i, cpoint+1:py)];
	else
		newpop(i, :) = pop(i,:);
		newpop(i+1,:) = pop(i+1,:);
	end
end

mutation.m(变异函数)

%变异
function [newpop] = mutation(pop, pm)
[px, py] = size(pop);
newpop = ones(size(pop));
for i = 1:px
	if(rand < pm)
		mpoint = round(rand*py);
		if mpoint <= 0
			mpoint = 1;
			
		end
		newpop(i,:) = pop(i,:);
		if newpop(i, mpoint) == 0
			newpop(i, mpoint) =1;
		else newpop(i, mpoint) == 1
			newpop(i, mpoint) = 0;
		end
		
	else
		newpop(i,:) = pop(i,:);
	end
end

best.m(选择最优个体函数)

%选择最优个体
function [bestindividual bestfit] = best(pop, fitvalue)

[px, py] = size(pop);
bestfit = fitvalue(1);
bestindividual = pop(1,:);
for i = 2:px
	if fitvalue(i) > bestfit
		bestfit = fitvalue(i);
		bestindividual = pop(i, :);
	end
end

实验结果：
迭代100次之后的图像：

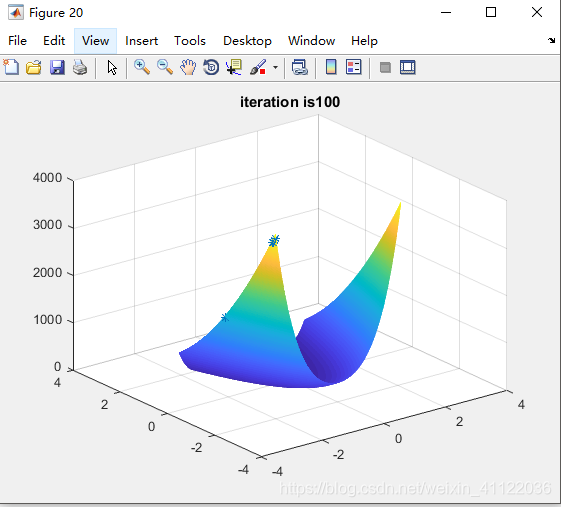
在这里插入图片描述

数据：

the best x1 is -->>-2.04
the best x2 is -->>-2.03
the best y is -->>3825.04

已经非常接近最大值的真实值（x1 = -2.048,x2 = -2.048）。
ps我是挑选的比较好的实验结果贴上来的，事实证明，这样计算也还是经常跑到另外一个极大值那边（x1 = 2.048 x2 = -2.048）。参数可以调节（种群数、交换概率、变异概率等），交换和变异方式也可以选择其他的方式，我还会继续学习其他的交换变异方式，完善这道题目。

对照实验：

使用lingo软件求解最大值：
程序：

model:

max = (1 - x1)^2 + 100*(x2 - x1^2)^2;

x1 >=-2.048;
x1 <= 2.048;
x2 >= -2.048;
x2 <= 2.048;

end

结果：

  Global optimal solution found.
  Objective value:                              1760.317
  Objective bound:                              1760.317
  Infeasibilities:                              0.000000
  Extended solver steps:                               0
  Total solver iterations:                            33

  Model Class:                                       NLP

  Total variables:                      2
  Nonlinear variables:                  2
  Integer variables:                    0

  Total constraints:                    5
  Nonlinear constraints:                1

  Total nonzeros:                       6
  Nonlinear nonzeros:                   2

                                Variable           Value        Reduced Cost
                                      X1        2.048000            0.000000
                                      X2        0.000000            838.8608

                                     Row    Slack or Surplus      Dual Price
                                       1        1760.317            1.000000
                                       2        4.096000            0.000000
                                       3        0.000000            3438.070
                                       4        2.048000            0.000000
                                       5        2.048000            0.000000

计算的最大值仅仅是1760.317，明显是局部最大值。
结论： 使用遗传算法，找到了函数的全局最优解。

2、求下文二元函数的最大值。

f(x1, x2) = x12 + x22;
x1∈{1， 2， 3， 4， 5}；x2∈{1， 2， 3， 4， 5}
和第一道题目类似，这道题目更简单。
思路：

  • 1、编码与解码：自变量都是整数且不超过7，那么每个自变量以3位二进制编码000-111∈[0， 7].那么每个个体就是六位二进制数。
  • 2、适应度函数：f(x1, x2) 恒大于0， 所以可以直接作为适应度函数。
  • 3、三种算子：选择复制使用轮盘赌法，交换和变异直接按照第一道题目的算法。
    matlab程序：
    main.m
function main()
clear;
clc;
%种群大小
popsize = 90;
%二进制编码长度
chromelength = 6;
%交叉概率
pc = 0.6;
%变异概率
pm = 0.001;
%初始种群 %pop = population 种群
pop = initpop(popsize, chromelength);

%迭代100次
for i = 1:100
	%计算适应度值?
	objvalue = cal_objvalue(pop);
	fitvalue = objvalue;	
	%选择复制
	newpop = selection(pop, fitvalue);
	%交换
	newpop = crossover(newpop, pc);
	%变异
	newpop = mutation(newpop, pm);
	%更新种群
	pop = newpop;
	%寻找最优解并打印在command窗口
	[bestindividual, bestfit] = best(pop, fitvalue);
	[x1b, x2b] = binary2decimal(bestindividual);
	fprintf('the best x1 is -->>%5.2f\n', x1b);
	fprintf('the best x2 is -->>%5.2f\n', x2b);
	fprintf('the best y is -->>%5.2f\n', bestfit);
	%更新后的种群
	[x1, x2] = binary2decimal(newpop);
	y = cal_objvalue(newpop);
	if mod(i ,10) == 0
		figure;
		x3 = 0:0.01:7;
		x4 = 0:0.01:7;
		[x5, x6] = meshgrid(x3, x4);
		y1 = x5.^2 + x6.^2;
		mesh(x5, x6, y1);
		hold on;
		plot3(x1, x2, y, '*');
		title(['iteration is ' num2str(i)]);
	end
end

initpop.m

%初始化种群
function pop = initpop(popsize, chromelength)
%随机产生90*20的0 1序列作为初始化种群
pop = round(rand(popsize, chromelength));

cal_value.m

%计算适应度函数
function objvalue = cal_objvalue(pop)

[x1, x2] = binary2decimal(pop);
objvalue = x1.^2 + x2.^2;

binary2decimal.m

%二进制转化为十进制
function [pop3 pop4] = binary2decimal(pop)
[px, py] = size(pop);
%计算x1的数值矩阵
for i= 1:py - 3
	pop1(:, i) = 2.^(py - 3 - i)*pop(:,i);
end
%计算x2的数值矩阵
for i = 4:py
	pop2(:, i - 3) = 2.^(py - i)*pop(:, i);
end	
%x1的十进制数值
pop3 = sum(pop1, 2);
%x2的十进制数值
pop4 = sum(pop2, 2);

selection.m

%选择和复制  轮盘赌法
function [newpop] = selection(pop, fitvalue)
[px, py] = size(pop);
totalfit = sum(fitvalue);
p_fitvalue = fitvalue/totalfit;
%概率求和排序
p_fitvalue = cumsum(p_fitvalue);
%产生随机概率并排序
ms = sort(rand(px, 1));
fitin = 1;
newin = 1;
while newin <= px
	if(ms(newin) < p_fitvalue(fitin))
		newpop(newin,:) = pop(fitin,:);
		newin = newin + 1;
		
	else
		fitin = fitin + 1;
	end
	
end

crossover.m

%交换
function [newpop] = crossover(pop, pc)
[px, py] = size(pop);
newpop = ones(size(pop));
%理论是随机交换（交换哪个，和谁交换，交换哪一部分都是随机的），这里采用i和i+1的随机部分交换，尽可能达到随机
for i = 1:2:px - 1
	if(rand < pc)
		cpoint = round(rand*py);
		newpop(i,:) = [pop(i,1:cpoint), pop(i+1, cpoint + 1:py)];
		newpop(i+1, :) = [pop(i+1,1:cpoint), pop(i, cpoint+1:py)];
	else
		newpop(i, :) = pop(i,:);
		newpop(i+1,:) = pop(i+1,:);
	end
end

mutation.m

%变异
function [newpop] = mutation(pop, pm)
[px, py] = size(pop);
newpop = ones(size(pop));
for i = 1:px
	if(rand < pm)
		mpoint = round(rand*py);
		if mpoint <= 0
			mpoint = 1;
			
		end
		newpop(i,:) = pop(i,:);
		if newpop(i, mpoint) == 0
			newpop(i, mpoint) =1;
		else newpop(i, mpoint) == 1
			newpop(i, mpoint) = 0;
		end
		
	else
		newpop(i,:) = pop(i,:);
	end
end

best.m


%选择最优个体
function [bestindividual bestfit] = best(pop, fitvalue)

[px, py] = size(pop);
bestfit = fitvalue(1);
bestindividual = pop(1,:);
for i = 2:px
	if fitvalue(i) > bestfit
		bestfit = fitvalue(i);
		bestindividual = pop(i, :);
	end
end

最终实验结果：
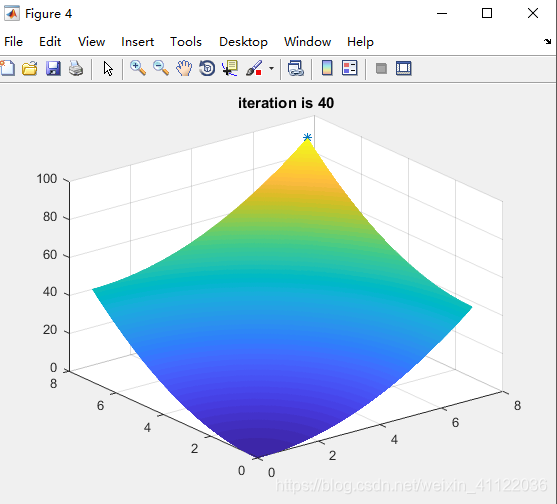
在这里插入图片描述

the best x1 is -->> 7.00
the best x2 is -->> 7.00
the best y is -->>98.00

迭代40次，效果就已经很好了。
当然，这道题目就是为了练习遗传算法，实际上可以使用lingo计算这种最优解。

对照实验：

使用lingo软件求解函数最大值：
程序：

model:

max = x1^2 + x2^2;

x1 > 0;
x1 <= 7;
x2 >0;
x2 <= 7;
@gin(x1);
@gin(x2);

end

结果：

  Global optimal solution found.
  Objective value:                              98.00000
  Objective bound:                              98.00000
  Infeasibilities:                              0.000000
  Extended solver steps:                               0
  Total solver iterations:                            13

  Model Class:                                     PINLP

  Total variables:                      2
  Nonlinear variables:                  2
  Integer variables:                    2

  Total constraints:                    5
  Nonlinear constraints:                1

  Total nonzeros:                       6
  Nonlinear nonzeros:                   2

                                Variable           Value        Reduced Cost
                                      X1        7.000000            0.000000
                                      X2        7.000000            0.000000

                                     Row    Slack or Surplus      Dual Price
                                       1        98.00000            1.000000
                                       2        7.000000            0.000000
                                       3        0.000000            14.00000
                                       4        7.000000            0.000000
                                       5        0.000000            14.00000

结论：两种方法找到的都是全局最优解。

3、多约束非线性规划问题

题目：
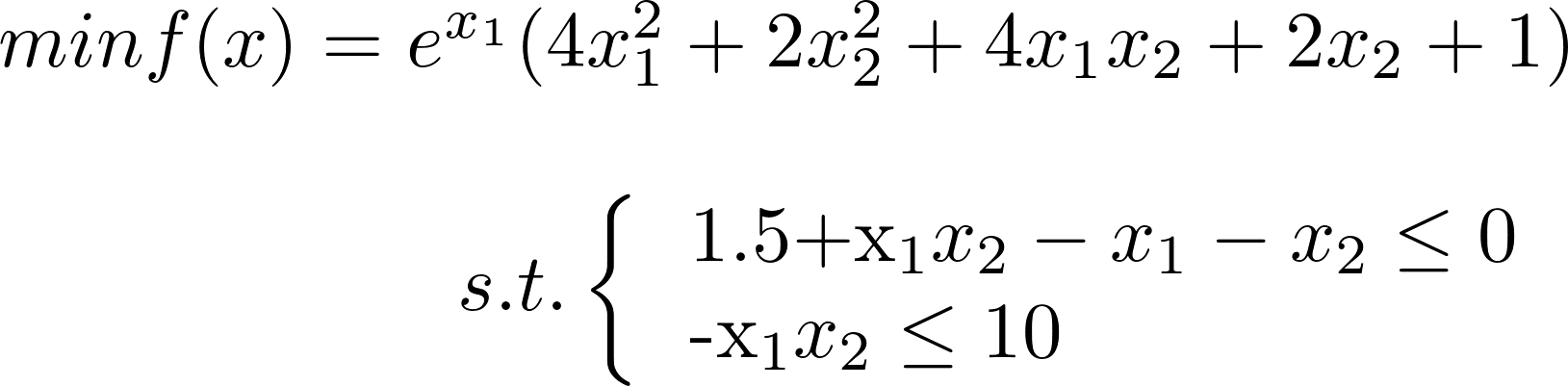
在这里插入图片描述
思路：

  • 1、编码与解码：自变量使用十位二进制数表示，自己定义数值范围，进行区域内的最小值计算。（原因：当x1和x2均大于0，那么f(x)几乎是呈指数式爆炸增长；当x1、x2均小于0时，函数的大趋势肯定也是增长的，最小值应该在x1和x2距离0不远的位置取得）
  • 2、适应度函数：这是求最小值的问题，和通常的最大值不同，不能直接使用f(x)适应度函数作为适应度函数，要进行一定的变换（变换宗旨：适应度函数大于等于0而且适应度越大，对应的函数值f(x)越小）。
    从课件中截图如下：
    在这里插入图片描述
    所以我的适应度函数处理方法是：f(x) < 100时，F(x) = 100 - f(x)；f(x) ≥100时，F(x) = 0.在写适应度函数时，加上约束的前提即可。
  • 3、 三种算子：均使用上边提到的方法。
    matlab程序：
    main.m
function main()
clear;
clc;
%种群大小
popsize = 100;
%二进制编码长度?
chromelength = 20;
%交叉概率
pc = 0.6;
%变异概率
pm = 0.001;
%初始种群 %pop = population 种群
pop = initpop(popsize, chromelength);
%迭代100次?
for i = 1:100
	%计算适应度
	objvalue = cal_objvalue(pop);
	fitvalue = objvalue;	
	%选择复制
	newpop = selection(pop, fitvalue);
	%交换
	newpop = crossover(newpop, pc);
	%变异
	newpop = mutation(newpop, pm);
	%更新种群
	pop = newpop;
	%最佳点
	[bestindividual, bestfit] = best(pop, fitvalue);
	[x1b, x2b] = binary2decimal(bestindividual);
	fb = exp(x1b).*(4*x1b.^2 + 2*x2b.^2 + 4*x1b.*x2b + 2*x2b + 1);
	%更新后的种群
	[x1, x2] = binary2decimal(newpop);
	y = cal_objvalue(newpop);
	f = exp(x1).*(4*x1.^2 + 2*x2.^2 + 4*x1.*x2 + 2*x2 + 1);
	%每迭代一次输出一次图像?
	if mod(i, 10) == 0
		figure;
		x3 = -10:0.1:10;
		x4 = -10:0.1:10;
		[x5, x6] = meshgrid(x3, x4);
		y1 = exp(x5).*(4*x5.^2 + 2*x6.^2 + 4*x5.*x6 + 2*x6 + 1);
		mesh(x5, x6, y1);
		hold on;
		plot3(x1, x2, f, '*');
		title([' iteration is ' num2str(i)]);
	end
end
fprintf('the best x1 is --->>%5.2f\n', x1b);
fprintf('the best x2 is --->>%5.2f\n', x2b);
fprintf('the best f is --->>%5.2f\n', fb);

initpop.m

%初始化种群
function pop = initpop(popsize, chromelength)
%随机产生90*20的0 1序列作为初始化种群
pop = round(rand(popsize, chromelength));

binary2decimal.m

%二进制转化为十进制
function [pop3 pop4] = binary2decimal(pop)

[px, py] = size(pop);
%计算x1的数值矩阵
for i = 1:py - 10
	pop1(:,i) = 2.^(py - 10 - i)*pop(:,i);
end
%计算x2的数值矩阵
for i = 11:py
	pop2(:,i - 10) = 2.^(py - i)*pop(:,i);
end
%x1求和后的列向量
temp1 = sum(pop1, 2);
%x2求和后的列向量 
temp2 = sum(pop2, 2);
%x1转换位十进制
pop3 = -10 + 20/1023*temp1;
%x2转换位十进制
pop4 = -10 + 20/1023*temp2;

cal_objvalue.m

%适应度函数

function objvalue = cal_value(pop)
[px, py] = size(pop);
[x1, x2] = binary2decimal(pop);
g1 = 1.5 + x1.*x2 - x1 - x2;
g2 = - x1.*x2;
%f值
f = exp(x1).*(4*x1.^2 + 2*x2.^2 + 4*x1.*x2 + 2*x2 + 1);

for i = 1:px
	%满足约束	
	if g1(i)<=0 && g2(i) <= 10
		%适应度函数
		if f(i) < 100
			objvalue(i) = 100 - f(i);
		else
			objvalue(i) = 0;
		end
	else
		objvalue(i) = 1;
	end
end

selection.m

%选择和复制  轮盘赌法
function [newpop] = selection(pop, fitvalue)
[px, py] = size(pop);
totalfit = sum(fitvalue);
p_fitvalue = fitvalue/totalfit;
%概率求和排序
p_fitvalue = cumsum(p_fitvalue);
%产生随机概率并排序
ms = sort(rand(px, 1));
fitin = 1;
newin = 1;
while newin <= px
	if(ms(newin) < p_fitvalue(fitin))
		newpop(newin,:) = pop(fitin,:);
		newin = newin + 1;
		
	else
		fitin = fitin + 1;
	end
	
end

crossover.m

%交换
function [newpop] = crossover(pop, pc)
[px, py] = size(pop);
newpop = ones(size(pop));
%理论是随机交换（交换哪个，和谁交换，交换哪一部分都是随机的），这里采用i和i+1的随机部分交换，尽可能达到随机
for i = 1:2:px - 1
	if(rand < pc)
		cpoint = round(rand*py);
		newpop(i,:) = [pop(i,1:cpoint), pop(i+1, cpoint + 1:py)];
		newpop(i+1, :) = [pop(i+1,1:cpoint), pop(i, cpoint+1:py)];
	else
		newpop(i, :) = pop(i,:);
		newpop(i+1,:) = pop(i+1,:);
	end
end

mutation.m

%变异
function [newpop] = mutation(pop, pm)
[px, py] = size(pop);
newpop = ones(size(pop));
for i = 1:px
	if(rand < pm)
		mpoint = round(rand*py);
		if mpoint <= 0
			mpoint = 1;
			
		end
		newpop(i,:) = pop(i,:);
		if newpop(i, mpoint) == 0
			newpop(i, mpoint) =1;
		else newpop(i, mpoint) == 1
			newpop(i, mpoint) = 0;
		end
		
	else
		newpop(i,:) = pop(i,:);
	end
end

best.m

%选择最优个体
function [bestindividual bestfit] = best(pop, fitvalue)

[px, py] = size(pop);
bestfit = fitvalue(1);
bestindividual = pop(1,:);
for i = 2:px
	if fitvalue(i) > bestfit
		bestfit = fitvalue(i);
		bestindividual = pop(i, :);
	end
end

实验结果：
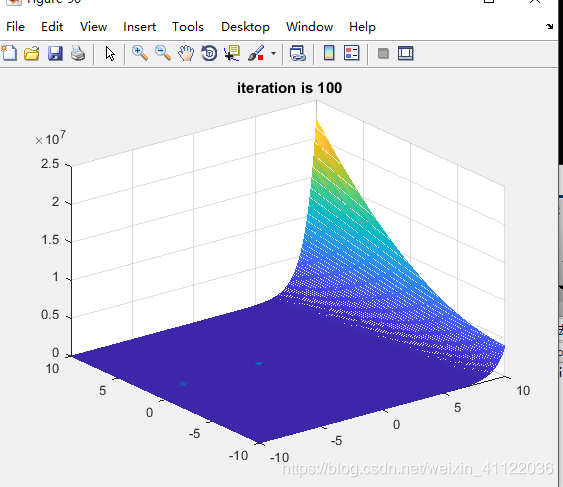
在这里插入图片描述
数据：

the best x1 is --->>-7.48
the best x2 is --->> 1.30
the best f is --->> 0.11
对照试验：

使用lingo求解函数最小值：
程序：

model:
!目标函数;
min = @exp(x1)*(4*x1^2 + 2*x2^2 + 4*x1*x2 + 2*x2 + 1);

!约束条件;
1.5 + x1*x2 - x1 - x2 <= 0;
- x1*x2 <= 10;

end

结果：

  Global optimal solution found.
  Objective value:                              8.500000
  Objective bound:                              8.500000
  Infeasibilities:                              0.000000
  Extended solver steps:                               3
  Total solver iterations:                            73

  Model Class:                                       NLP

  Total variables:                      2
  Nonlinear variables:                  2
  Integer variables:                    0

  Total constraints:                    3
  Nonlinear constraints:                3

  Total nonzeros:                       6
  Nonlinear nonzeros:                   6

                                Variable           Value        Reduced Cost
                                      X1        0.000000            18.50000
                                      X2        1.500000            0.000000

                                     Row    Slack or Surplus      Dual Price
                                       1        8.500000           -1.000000
                                       2        0.000000            8.000000
                                       3        10.00000            0.000000

结论： 遗传算法找到了全局最优解。

4、 遗传算法解决旅行商问题。

遗传算法详解博文
这里边写的很清楚，源代码实验结果都有。
我加了一部分注释，程序如下：

% 利用遗传算法，解决TSP问题模板
tic  %tic toc 用来计算程序段运行的时间
clc,clear
sj = load('gadata.txt'); %加载敌方100 个目标的数据 sj = 25*8  输入数据是精度和纬度信息
x=sj(:,1:2:8);x=x(:); %x为经度 x = 100*1
y=sj(:,2:2:8);y=y(:); %y为纬度 y = 100*1
sj=[x y]; %sj = 100*2  sj(1)经度，sj(2)纬度
figure(1);
plot(x,y);
xlabel('longtitude');
ylabel('latitude');%画出初始图形
d1=[70,40];%初始点
sj0=[d1;sj;d1];%sj0 102*2
%距离矩阵d
sj=sj0*pi/180; %变为弧度制
d=zeros(102);%距离矩阵初始化 d 102*102
for i=1:101
    for j=i+1:102
        temp=cos(sj(i,1)-sj(j,1))*cos(sj(i,2))*cos(sj(j,2))+sin(sj(i,2))*sin(sj(j,2));
        d(i,j)=6370*acos(temp);
    end
end
d=d+d';L=102;w=50;dai=100;
%通过改良圈算法选取优良父代A
for k=1:w
    c=randperm(100);
    c1=[1,c+1,102];
    flag=1;
    while flag>0
        flag=0;
        for m=1:L-3
            for n=m+2:L-1
                if d(c1(m),c1(n))+d(c1(m+1),c1(n+1))<d(c1(m),c1(m+1))+d(c1(n),c1(n+1))
                    flag=1;
                    c1(m+1:n)=c1(n:-1:m+1);
                end
            end
        end
    end
    J(k,c1)=1:102;
end
J=J/102;
J(:,1)=0;J(:,102)=1;
rand('state',sum(clock));
%遗传算法实现过程
A=J;
for k=1:dai %产生0～1 间随机数列进行编码
    B=A;
    c=randperm(w);
    %交配产生子代B
    for i=1:2:w
        F=2+floor(100*rand(1));
        temp=B(c(i),F:102);
        B(c(i),F:102)=B(c(i+1),F:102);
        B(c(i+1),F:102)=temp;
    end
    %变异产生子代C
    by=find(rand(1,w)<0.1);
    if length(by)==0
        by=floor(w*rand(1))+1;
    end
    C=A(by,:);
    L3=length(by);
    for j=1:L3
        bw=2+floor(100*rand(1,3));
        bw=sort(bw);
        C(j,:)=C(j,[1:bw(1)-1,bw(2)+1:bw(3),bw(1):bw(2),bw(3)+1:102]);
    end
    G=[A;B;C];
    TL=size(G,1);
    %在父代和子代中选择优良品种作为新的父代
    [dd,IX]=sort(G,2);temp(1:TL)=0;
    for j=1:TL
        for i=1:101
            temp(j)=temp(j)+d(IX(j,i),IX(j,i+1));
        end
    end
    [DZ,IZ]=sort(temp);
    A=G(IZ(1:w),:);
end
path=IX(IZ(1),:)
long=DZ(1)
toc
xx=sj0(path,1);yy=sj0(path,2);
%plot(xx,yy,'-o',)
figure(2);
plot(xx,yy,'-o');
xlabel('longtitude');
ylabel('latitude');

事实证明，遗传算法思想并不难，就是建模时候的处理方式，编码方式的选择（二进制，十进制，格雷码等），适应度函数的确定（函数必须大于0，以确定轮盘赌选择法的正确性），以及交换和变异的写法（随机很重要）等需要不断地摸索以积累经验，力求获得全局最优解。

猜你喜欢

转载自blog.csdn.net/weixin_41122036/article/details/99621870
今日推荐
面壁智能发布 Eurux-8x22B 开源大模型 —— 堪称「理科状元」
开源日报 | 谷歌扶持鸿蒙上位；开源Rabbit R1；Docker加持的安卓手机；微软的焦虑和野心；海尔电器把开放平台关了
中国码农的“35岁魔咒”
蘭雅 CorelDRAW 插件 2024.5.1 国际劳动节版，免费下载
Arc Browser for Windows 1.0 正式 GA
90后程序员开发视频搬运软件、不到一年获利超 700 万，结局很刑！
周排行
【转】spring中对控制反转和依赖注入的理解
tms webcore 安装和使用
java程序员进阶相关书籍
SpringMVC接受请求参数、
如何保存训练好的机器学习模型
MyEclipse、Eclipse设置项目JDK的三个地方
商超行业微信小程序开发定制一般多少钱 （行业技术人员解读）
Markdown编辑器语言——30分钟入门到到精通
Linux系统下MongoDB的简单安装与基本操作
Power Strings
每日归档
更多
2024-05-07(14)
2024-05-06(40)
2024-05-05(0)
2024-05-04(7)
2024-05-03(19)
2024-05-02(0)
2024-05-01(4)
2024-04-30(1)
2024-04-29(40)
2024-04-28(0)

代码天地 © 2018 codetd.com

境外服务器   最新电视剧2022