子集生成（子集树+递归回溯）

本文链接： https://blog.csdn.net/Africa_South/article/details/102612501

文章目录

1.问题定义
2. 增量构造法
3. 位向量法
3. 二进制法
4. 例题收录

1.问题定义

给定一个集合，枚举所有可能的子集，为了简单起见，假设集合中的元素不重复。则 $n$ 个元素的集合会有 $2^n$ 个子集，而且不相同。
下列算法均以生成 {1,2,…,n}的子集为例。

2. 增量构造法

void subset1(int* A, int n,int cur) {
	/* n为原集合的元素个数，cur为当前生成集合的长度*/
	for (int i = 0; i < cur; i++) printf("%d ", A[i]);
	printf("\n"); // 先打印已有集合
	int s = cur ? A[cur - 1] + 1 : 1; // 确定下一可选元素的最小值
	for (int i = s; i <= n; i++) {
		A[cur] = i;// 从1开始
		subset1(A, n, cur + 1); // 递归构造子集
	}
}

上面的代码使用了一个定序的技巧，即先将数组A进行排序，然后每次枚举的时候都枚举比当前大的下标元素。即枚举过{1,2}就不会枚举{2,1}了。
之所以叫增量构造法，是因为集合A中的元素个数是不确定的，而我们是按照元素个数从小到大构造的，即我们能得到如下解答树：（以 $n=3$ 为例）
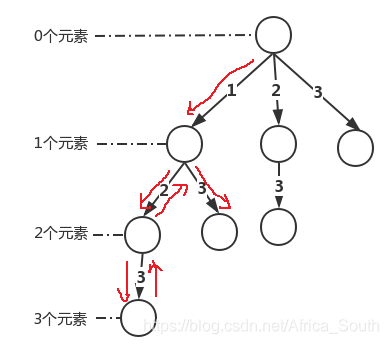
上树种一共有8个结点，对应于n=3的8个子集，即 树中每个结点都是一个解，而且每一层的子集的元素个数相同，一般的对于有n个元素的集合，其有 $C_n^0 + C_n^1 +...+C_n^n = (1+1)^n=2^n$ 个子集，即解答树含有 $2^n$ 个结点。

3. 位向量法

第二种方法是不直接构造子集A本身，而是构造一个位向量vis[]，即 $vis[i] = 1,当i在子集A中;否则vis[i] = 0$ ，则对于n个元素的集合，我们需要构造长度为n的位向量。

void subset2(int* vis, int n, int cur) {
	if (cur == n) {
		for (int i = 0; i < n; i++) {
			if (vis[i]) cout << i + 1 << " ";
		}
		cout << endl;
		return;
	}
	vis[cur] = 1; // 包含该元素
	subset2(vis, n, cur + 1);
	vis[cur] = 0; // 不包含该元素
	subset2(vis, n, cur + 1);
	return;
}

对于位向量法，我们也能画出一个解答树，来刻画我们的求解过程：（还是以n=3为例）
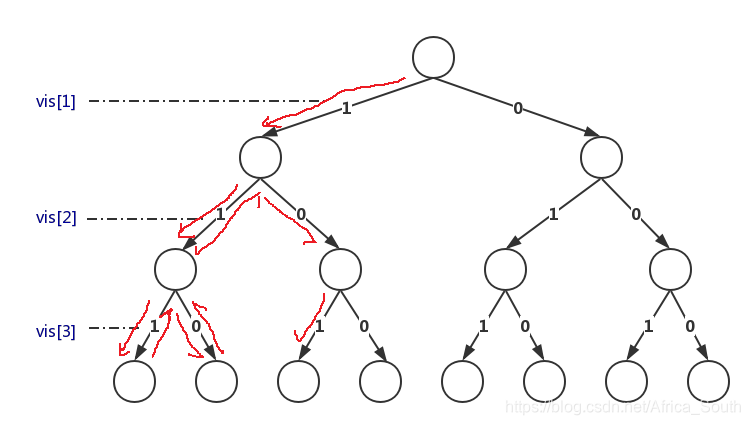
不难看出该解答树一共有8个叶子结点，对应于8种子集对应的位向量，即每个叶子结点都对应于一个解。一般的，对应于有n个元素的解答树我们有 $2*2*2...*2 = 2^n$ 个子集（叶子结点），算法中间结点比增量构造法多，但是多数情况下够快。

3. 二进制法

在位向量法 种我们用一个位向量来表示最终的结果，由于一个位置的取值只会是0或1，则我们可以用二进制来表示我们的结果。即对于集合 $S = \{0,1,2,3,...,n-1\}$ ，我们用一个二进制数从右往左第 $i$ 位表示元素 $i$ 是否在集合S中（个位从0开始编号）。
例如，下图用二进制 $0100-0110-0011-0111$ 来表示集合 $\{0,1,2,4,5,9,10,14\}$
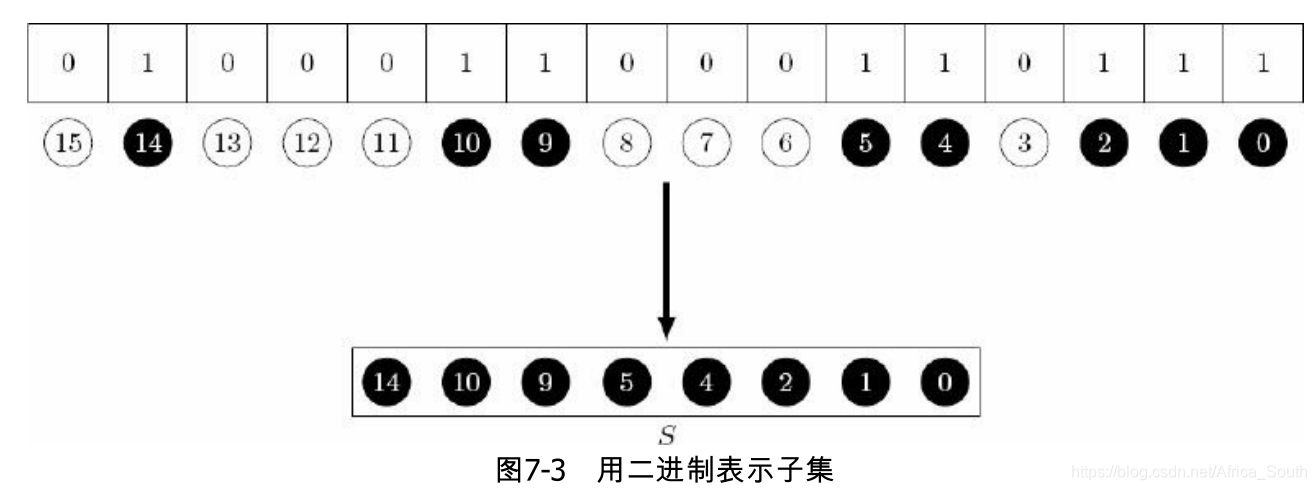
在这里插入图片描述
注意：为了处理方便，最右面的元素编号为0

使用二进制表示子集有一个很大的好处，即集合间的操作能够用二进制的位操作来替换。

C语言中常见的二元位运算与（&）、或（|）、非（！）、异或（^）的真值表：

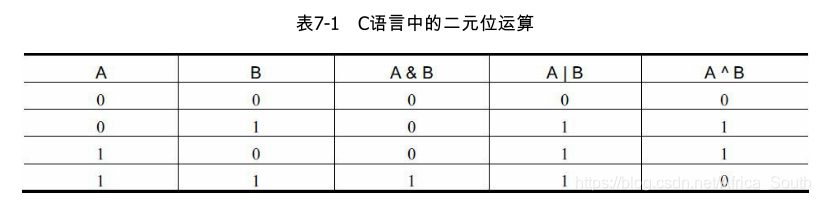
其中 与1进行异或相等于取相反数，即异或的规则是相同为0，不同为1。且 0^1=1,1^1=0
而位运算与、或、异或对应于集合操作中的交、并、对称差。
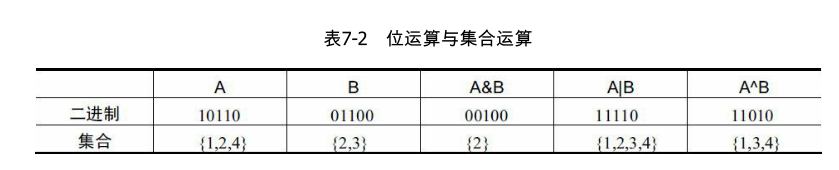
特别地，对于有n个元素的全集我们定义为 ALL = (1<<n) - 1，即n个1；
A的补集定义为ALL ^ A，而不是非运算。
而代码实现看起来非常的简洁

void print_subset3(int n, int s) {
	/* n为位向量长度，s为该位向量 */
	for (int i = 0; i < n; i++) {
		if (s & (1 << i)) printf("%d ", i);
	}
	printf("\n");
}
// 二进制法枚举
void subset3(int n) {
	for (int i = 0; i < (1 << n); i++)// 构造位向量
		print_subset3(n, i);
}

4. 例题收录

UVA 1354 Mobile Computing

参考资料
《算法竞赛入门第二版》