D. Power Tower
time limit per test
4.5 seconds
memory limit per test
256 megabytes
input
standard input
output
standard output
Priests of the Quetzalcoatl cult want to build a tower to represent a power of their god. Tower is usually made of power-charged rocks. It is built with the help of rare magic by levitating the current top of tower and adding rocks at its bottom. If top, which is built from k - 1 rocks, possesses power p and we want to add the rock charged with power *w**k* then value of power of a new tower will be {*w**k}p*.
Rocks are added from the last to the first. That is for sequence w1, ..., *w**m* value of power will be
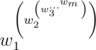
After tower is built, its power may be extremely large. But still priests want to get some information about it, namely they want to know a number called cumulative power which is the true value of power taken modulo m. Priests have n rocks numbered from 1 to n. They ask you to calculate which value of cumulative power will the tower possess if they will build it from rocks numbered l, l + 1, ..., r.
Input
First line of input contains two integers n (1 ≤ n ≤ 105) and m (1 ≤ m ≤ 109).
Second line of input contains n integers *w**k* (1 ≤ *w**k* ≤ 109) which is the power of rocks that priests have.
Third line of input contains single integer q (1 ≤ q ≤ 105) which is amount of queries from priests to you.
*k**th* of next q lines contains two integers *l**k* and *r**k* (1 ≤ lk ≤ rk ≤ n).
Output
Output q integers. k-th of them must be the amount of cumulative power the tower will have if is built from rocks lk, lk + 1, ..., *r**k*.
Example
input
Copy
6 10000000001 2 2 3 3 381 11 62 22 32 44 44 54 6output
Copy
1124256327597484987Note
327 = 7625597484987
思路:

因为euler( euler(x) ) <= x/2 所以在log(x)次内欧拉函数值就会降为1,并且一直为1.而任何数对1取模的答案都是0,所以我们可以遇见模数为1时就可以结束迭代,
因此每次询问最多迭代log(m)次,每一次迭代只需要一个快速幂的时间复杂度,也是log(m)
因此对于每一个询问综合的时间复杂度是O(log(m)^2)
注意,在指数循环节中快速幂时,需要在ans>=mod时,取模后再加上mod,以此才满足欧拉降幂定理。
细节见代码:
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cmath>
#include <queue>
#include <stack>
#include <map>
#include <set>
#include <vector>
#include <iomanip>
#define ALL(x) (x).begin(), (x).end()
#define sz(a) int(a.size())
#define all(a) a.begin(), a.end()
#define rep(i,x,n) for(int i=x;i<n;i++)
#define repd(i,x,n) for(int i=x;i<=n;i++)
#define pii pair<int,int>
#define pll pair<long long ,long long>
#define gbtb ios::sync_with_stdio(false),cin.tie(0),cout.tie(0)
#define MS0(X) memset((X), 0, sizeof((X)))
#define MSC0(X) memset((X), '\0', sizeof((X)))
#define pb push_back
#define mp make_pair
#define fi first
#define se second
#define eps 1e-6
#define gg(x) getInt(&x)
#define chu(x) cout<<"["<<#x<<" "<<(x)<<"]"<<endl
using namespace std;
typedef long long ll;
ll gcd(ll a, ll b) {return b ? gcd(b, a % b) : a;}
ll lcm(ll a, ll b) {return a / gcd(a, b) * b;}
inline void getInt(int* p);
const int maxn = 1000010;
const int inf = 0x3f3f3f3f;
/*** TEMPLATE CODE * * STARTS HERE ***/
ll mod(ll x, ll m)
{
return x >= m ? x % m + m : x;
}
ll powmod(ll a, ll b, ll MOD)
{
ll ans = 1;
while (b)
{
if (b % 2)
ans = mod(ans * a, MOD);
// ans = ans * a % MOD;
// a = a * a % MOD;
a = mod(a * a, MOD);
b /= 2;
}
return ans;
}
ll m;
int n;
int q;
ll a[maxn];
map<ll, ll> vis;
ll euler(ll n) { //log(n)时间内求一个数的欧拉值
if (vis.count(n))
{
return vis[n];
}
ll ans = n;
for (ll i = 2; i * i <= n; i++) {
if (n % i == 0)
{
ans -= ans / i;
while (n % i == 0) n /= i;
}
}
if (n > 1) ans -= ans / n;
vis[n] = ans;
return ans;
}
ll solve(int l, int r, ll m)
{
if (l == r || m == 1)
return mod(a[r], m);
return powmod(a[l], solve(l + 1, r, euler(m)), m);
}
int main()
{
//freopen("D:\\common_text\\code_stream\\in.txt","r",stdin);
//freopen("D:\\common_text\\code_stream\\out.txt","w",stdout);
// gbtb;
// cin >> n >> m;
scanf("%d%lld", &n, &m);
repd(i, 1, n)
{
scanf("%lld", &a[i]);
// cin >> a[i];
}
// cin >> q;
scanf("%d", &q);
int l, r;
while (q--)
{
scanf("%d %d", &l, &r);
printf("%lld\n", solve(l, r, m) % m);
// cin >> l >> r;
// cout << solve(l, r, m) % m << endl;
}
return 0;
}
inline void getInt(int* p) {
char ch;
do {
ch = getchar();
} while (ch == ' ' || ch == '\n');
if (ch == '-') {
*p = -(getchar() - '0');
while ((ch = getchar()) >= '0' && ch <= '9') {
*p = *p * 10 - ch + '0';
}
}
else {
*p = ch - '0';
while ((ch = getchar()) >= '0' && ch <= '9') {
*p = *p * 10 + ch - '0';
}
}
}