BZOJ 1002: [FJOI2007]轮状病毒 递推+高精度模板

title

BZOJ 1002
LUOGU 2144
Description

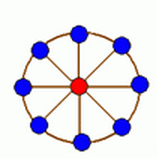
　　轮状病毒有很多变种，所有轮状病毒的变种都是从一个轮状基产生的。一个N轮状基由圆环上N个不同的基原子
和圆心处一个核原子构成的，2个原子之间的边表示这2个原子之间的信息通道。如下图所示

　　N轮状病毒的产生规律是在一个N轮状基中删去若干条边，使得各原子之间有唯一的信息通道，例如共有16个不
同的3轮状病毒，如下图所示

现给定n(N<=100)，编程计算有多少个不同的n轮状病毒

Input

　　第一行有1个正整数n

Output

　　计算出的不同的n轮状病毒数输出

Sample Input

3

Sample Output

16

analysis

网上大多数人的做法应该是什么基尔霍夫矩阵，但是我没学过，也实在不想学了，就参照洛谷上第一个题解的方法了。

事实证明，花些时间打个表还是有些用的，当然，如果会 \(Matrix-Tree\)矩阵树定理的话，就不用很辛苦的画图了。

打表可知：
| \(n\) | \(ans\) |
|--|--|
| 1 | 1 |
|2|5|
|3|16|
|4|45|
|5|121|
于是可以发现：偶数项为 5 的倍数，奇数项都为完全平方数，那就把他们都展开。
| \(n\) | \(ans\) |
|--|--|
| 1 | 11|
|2|33-4|
|3|44|
|4|77-4|
|5|11*11|
我们把完全平方数的底数拿出来，是这样的：

1 3 4 7 11

于是又可以发现，这就是个变形的\(Fibonacci\)数列，只需要在偶数项的时候减去 4 即可。

那么总递推式就好了：
\[F[n]=f[n]*f[n]-4*(n+1~ mod ~2), f[n]=f[n-1]+f[n-2], f[1]=1, f[2]=3\]

\[f[i]表示这一项的完全平方数底数，F[i]表示这一项的答案\]

就这样解决了。

code

#include<bits/stdc++.h>
using namespace std;
const int maxn=101;

char buf[1<<15],*fs,*ft;
inline char getc() { return (ft==fs&&(ft=(fs=buf)+fread(buf,1,1<<15,stdin),ft==fs))?0:*fs++; }
template<typename T>inline void read(T &x)
{
    x=0;
    T f=1, ch=getchar();
    while (!isdigit(ch) && ch^'-') ch=getchar();
    if (ch=='-') f=-1, ch=getchar();
    while (isdigit(ch)) x=(x<<1)+(x<<3)+(ch^48), ch=getchar();
    x*=f;
}

template<typename T>inline void write(T x)
{
    if (!x) { putchar('0'); return ; }
    if (x<0) putchar('-'), x=-x;
    T num=0, ch[20];
    while (x) ch[++num]=x%10+48, x/=10;
    while (num) putchar(ch[num--]);
}

struct Orz
{
    int a[maxn*10], len;
    Orz()//定义时自动清空
    {
        len=0;
        memset(a,0,sizeof(a));
    }

    inline void init(int x)//用来给大整型变量赋整型值
    {
        len=0;
        while (x)
        {
            a[++len]=x%10;
            x/=10;
        }
    }

    inline Orz operator + (const Orz x) const//高精加
    {
        Orz ans;
        for (int i=1; i<=max(len,x.len); ++i) ans.a[i]=a[i]+x.a[i];
        for (int i=1; i<=max(len,x.len); ++i)
            if (ans.a[i]>=10) ans.a[i+1]+=ans.a[i]/10, ans.a[i]%=10;
        ans.len=max(len,x.len);
        if (ans.a[ans.len+1]) ++ans.len;//
        return ans;
    }

    inline Orz operator - (const Orz x) const//高精减
    {
        Orz ans;
        for (int i=1; i<=max(len,x.len); ++i) ans.a[i]=a[i]-x.a[i];
        for (int i=1; i<=max(len,x.len); ++i)
            if (ans.a[i]<0) ans.a[i+1]-=ans.a[i]/10, ans.a[i]%=10;
        ans.len=max(len,x.len);
        if (ans.a[ans.len+1]) ++ans.len;//
        return ans;
    }

    inline Orz operator / (const int x) const//高精除
    {
        Orz ans;
        int num=0;
        for (int i=len; i; --i)
        {
            num=num*10+a[i], ans.a[i]=num/x, num%=x;
            if (!ans.len && ans.a[i]) ans.len=i;
        }
        return ans;
    }

    inline Orz operator * (const Orz x) const//高精乘
    {
        Orz ans;
        for (int i=1; i<=len; ++i)
            for (int j=1; j<=x.len; ++j)
            {
                ans.a[i+j-1]+=a[i]*x.a[j];
                ans.a[i+j]+=ans.a[i+j-1]/10;
                ans.a[i+j-1]%=10;
            }
        ans.len=len+x.len-1;
        if (ans.a[ans.len+1]) ++ans.len;
        return ans;
    }
}ans, ans1, ans2, D;

inline void print(Orz x)//大型整数输出
{
    for (int i=x.len; i; --i) write(x.a[i]);
    puts("");
}

int main()
{
    int n;read(n);
    if (n==1) return puts("1"),0;
    if (n==2) return puts("5"),0;//特判的两个F[1]和F[2]
    ans1.init(1), ans2.init(3), D.init(4);//f[1]=1, f[2]=3
    for (int i=3; i<=n; ++i) ans=ans1+ans2, ans1=ans2, ans2=ans;//求f[n]，变形的Fibonacci数列
    if (n&1) ans=ans*ans;//F[n]=f[n]*f[n]-4*(n+1 mod 2), f[n]=f[n-1]+f[n-2], f[1]=1, f[2]=3
    else ans=ans*ans-D;
    print(ans);
    return 0;
}

summary

1. 通过这道题，把高精模板彻底固定了下来，以后就不怂了。
2. 忘了特判前两个答案，导致这道题一直 90，所以以后这种题目，又可以特判的，一定要特判，否则这苦向谁说去。
3. 有些知识还是要会的，方便打表，就像这个矩阵树定理。