数论入门基础整理

（有误欢迎大佬斧正）

基本定理：

威尔逊定理:一个数p为素数的充要条件是p|(p-1)!+1

费马小定理:对于素数p，以及整数a，如有(a,p)=1,则a^(p-1)=1(mod p)

欧拉定理:对于任意两个互素整数a,m ，a^φ(m) =1 (mod m), φ为欧拉函数，表示小于p且与p互素的数个数

欧拉函数求解：

 1 int euler(int x)
 2 {
 3     int res = x, n = x;
 4     for (int i = 2; i * i <= n; i++)
 5         if (n % i == 0)
 6         {
 7             res = res / i * (i - 1);
 8             while (n % i == 0)
 9                 n /= i;
10         }
11     if (n > 1)
12         res = res / n * (n - 1);
13     return res;
14 }

求一个欧拉函数值

1 void getEuler()
2 {
3     for (int i = 1; i < maxn; i++)
4         e[i] = i;
5     for (int i = 2; i < maxn; i++)
6         if (e[i] == i)
7             for (int j = i; j < maxn; j += i)
8                 e[j] = e[j] / i * (i - 1);
9 }

筛法求区间每个数欧拉函数

扩展欧拉定理:将欧拉定理延申到了 (a,m) !=1 的情况，可用于大指数运算

 <code>

孙子定理(中国剩余定理):

对于形如的方程组，m互素

令M=m₁*m₂..m_n, M_i = M/m_i, t_i=M_i在模m_i意义下的乘法逆元(关于乘法逆元可以参考费马小定理或扩展欧几里得算法)，解为

x=a₁*t₁*M₁+a₂*t₂*M₂+...a_n*t_n*M_n+kM，k为整数，原方程最小解为x mod M

对于m不互素的情况，需要用扩展欧几里得进行两两合并求解（埋坑）

<code>

---

素数与合数：

唯一分解定理:一个自然数x可以唯一分解为x = p₁^r₁p₂^r₂...p_n^r_n  (p为素数，r为正整数）

x的所有因子个数：(1 + r₁) * ( 1 + r₂ )...( 1 + r_n )

x的所有因子之和：( 1 + p₁ + p₁2 + p₁3...p₁r1)( 1 + p₂ + p₂2  +...+p₂^r₂)...( 1 + p_n + p_n² + ...+ p_n^r_n)

x的所有素因子之和: phi(n)*n/2, （phi为欧拉函数，表示小于n且与n互素的数个数）

反素数: 定义g(x)为x的因子个数，若对于所有的0 < i< x，都有g(i)<g(x)则称x为反素数

反素数性质1:一个反素数的素因子必然是从2开始的连续素数

反素数性质2:若n为反素数，则n= p₁^r₁p₂^r₂...p_n^r_n ,其中r1>=r2>=..rn

N!的素因子分解:

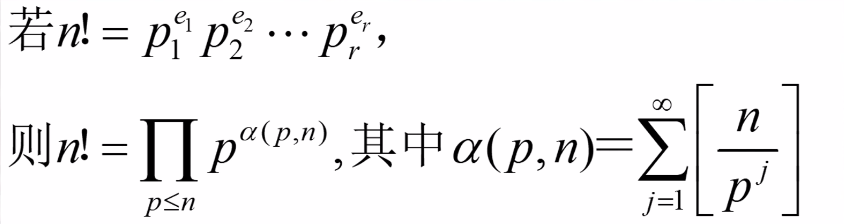
即幂可由后边和式计算得到

 <code>

埃氏筛素数（no code）

 

 1 for (int i = 2; i <= maxn; i++)
 2 {
 3     if (!vis[i])
 4         prime[pcnt++] = i;
 5     for (int j = 0; j < pcnt && i * prime[j] <= maxn; j++)
 6     {
 7         vis[i * prime[j]] = 1;
 8         if (i % prime[j] == 0)
 9             break;
10     }
11 }

欧拉筛素数

MIller-Robin素数测试法

费马小定理：对于素数p和任意整数a，若(a,p)=1,有a^p-1 ≡ 1 (mod p)。相反的，满足a^p-1 ≡ 1 (mod p)，p也几乎一定是素数。

伪素数：如果n是一个正整数，如果存在和n互素的正整数a满足 a^n-1 ≡ 1(mod n)，我们说n是基于a的伪素数。如果一个数是伪素数，那么它几乎肯定是素数。

Miller-Rabin测试：不断选取不超过n-1的基b(s次)，计算是否每次都有b^n-1 ≡ 1(mod n)，若每次都成立则n是素数，否则为合数。　

 <code>

Pollard-rho大数分解

--摘自大佬博客https://blog.csdn.net/Sunshine_cfbsl/article/details/52512706

对于一个大整数n，我们取任意一个数x使得x是n的质因数的几率很小，但如果取两个数x1以及x2使得它们的差是n的因数的几率就提高了，如果取x1以及x2使得gcd(abs(x1−x2),n)>1的概率就更高了。这就是Pollard-Rho算法的主要思想。

对于满足gcd(abs(x1−x2),n)>1的x1和x2，gcd(abs(x1−x2),n)就是n的一个因数，只需要判断它是否为素数，若为素数，则是n的质因数，否则递归此过程。

其中判断素数就使用MillerMiller-RabinRabin算法。

那么我们怎样不断取得x1x1和x2x2呢？
x1在区间[1,n]中随机出来，而x2则由x[i]=(x[i-1]*x[i-1]%n+c)%n推算出来，其中c为任意给定值，事实证明，这样就是比较优的。

<code>

莫比乌斯反演

（埋坑）

原根

（埋坑）