先是高精除法
注意细节
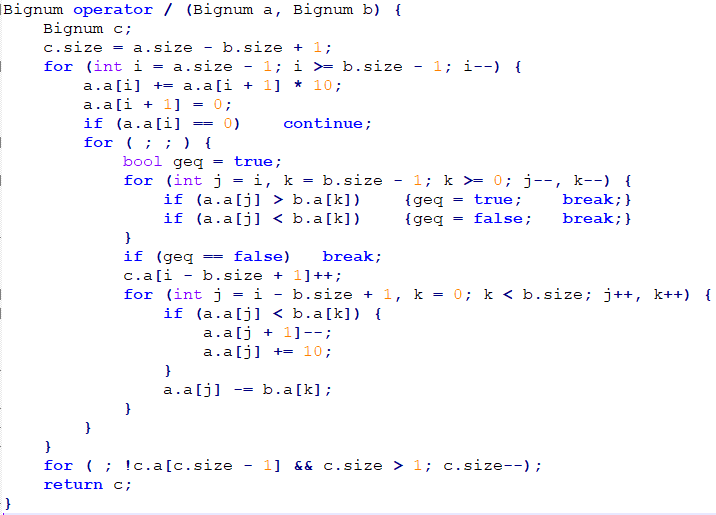
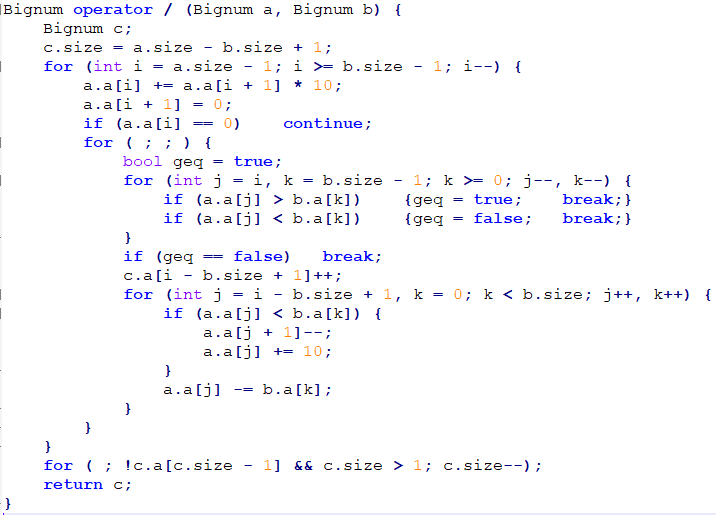
高精度开方:神奇的竖式
以小数点为分界线,每两个位砍一刀
87654.321-->08|76|54|.32|1


大概就是先对第一位开方,然后相减,将上面的数乘二十,看看加多少再乘多少正好不能撑爆剩下的数,就在上面写几,重复操作就ok
原理是: (a*10+b)^2=a^2+2*a*10*b+b^2=a^2+(20*a+b)*b
竖式算开平方步骤:(如:把625开方)
(1)先把被开方的数由右到左每二位一组。(6,25)
(2)由左到右取每一组。(取的是6)
(3)取某数的平方,要比第一组数小,但某数+1的平方,要比第一组数大,这就是第一个开方值。(某数是2)
(4)把第一组数减去第一个开方值的平方,再取第二组数,构成余数。(6-2*2=2,余数为225)
(5)把第一个开方值*20,再加上估计的第二个开方值,它与第二个开方值相乘要比余数小,但把第一个开方值*20,再加上估计的第二个开方值+1,它与第二个开方值+1相乘要比余数大。(第二个开方值取5,2*20+5=45,45*5=225)
所以(625)^0.5=25
现在中考高考都不让带计算器了,试卷上出现的一些常见开方的数字都是直接提供给学生的。现在手工列竖式开方基本不再需要了,但是每每想起当时老师教过的列式开平方的方法,还是很骄傲的。
手工开平方的原理实际是很简单的,原理如下
(a+b)^2=a^2+2ab+b^2=a^2+(2a+b)*b
这里的a取10的倍数,b取个位数,如(10+2)^2=10^2+(2*10+2)*2=100+22*2=144,这是知道结果时的推算,如何给你一个数字,让你推算它的开平方值呢?
现在要对144开平方,那么估计所求的值为十几,因此可以写成(10+?)^2=10^2+(2*10+?)*?,这样猜这个?为2时,再代入计算,发现计算出的值正确。按此方法,可以列竖式进行计算。如果需要对2025进行开方处理,那么按两位两位进位,需要先对20求根,取5时,5*5>20,因此只能取4,也就是结果是四十几,即(40+?)^2=40^2+(2*40+?)*?,即减去40的平方1600后,2025还余下425,425再去除于8?(八十几),才能得到?(几),结论当然是85*5=425,因此2025开平方就是45。
。
快速幂

矩阵乘法
一个i行k列的矩阵乘一个k行j列的矩阵得到一个i行j列的矩阵
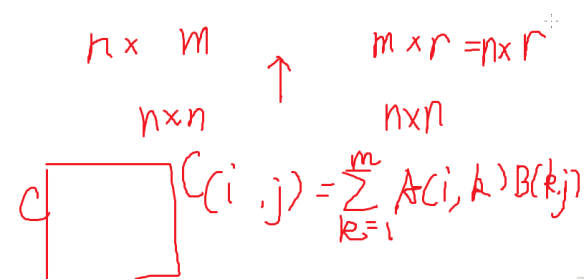
答案矩阵的第i,j个元素为A矩阵第i行第k个元素乘B矩阵第k行第j个元素,k是从1到m
就是一个矩阵的行乘另一个矩阵的列
代码:
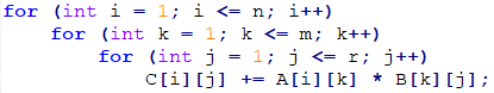
矩阵快速幂常用于求解线性递推方程组
比如斐波那契数列的矩阵就是
1 1
1 0
[f[n],f[n-1]]*[矩阵]^k=[f[n+k],[n+k-1]]
矩阵快速幂基于以下的原理,即可以找到一个矩阵 M
使得 [F(n-1) F(n)]T* M = [F(n) F(n+1)]T
以斐波拉期数列为例:M = ((1 1) (1 0))
以此类推:
[F(0) F(1)]T* Mn = [F(n) F(n+1)]T
我们成功将一个递推式转化成了一个求矩阵幂的问题
利用快速幂算法可以将时间缩短为 O(d^3logn)
利用 FFT + 矩阵特征多项式的黑科技可以把时间进一步缩短到 O(dlogdlogn)
我们来试着写一下下面的矩阵:
F(n) = 7F(n-1) + 6F(n-2) + 5n + 4 * 3^n
先考虑转换前后的两个矩阵,肯定要有所有在转换中需要的
我们发现如果要从f[n-1]转换到f[n],要用到f[n-1],f[n-2],n,3^n,我们就先写上这些
然后发现n要转换到n+1就需要个1,再加上1就好了
[f[n-1,] f[n-2,] n, 3^n, 1]
[f[n], f[n-1], n+1, 3^(n+1) ,1]
然后按照递推式搞一搞就ok
高斯消元
高斯消元可以将一个矩阵变成一个上三角矩阵
在 OI 中一般用于两点:求解线性方程组(不常见) & 求线性基(常见)
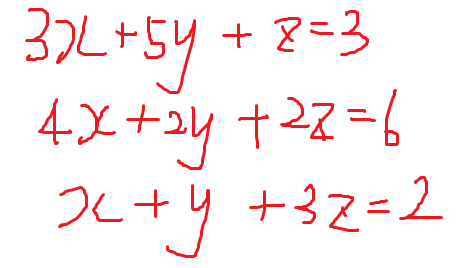
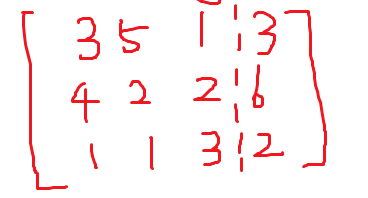

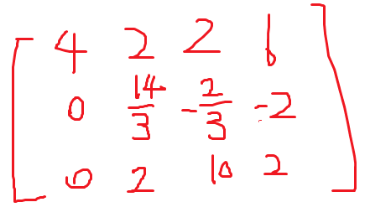

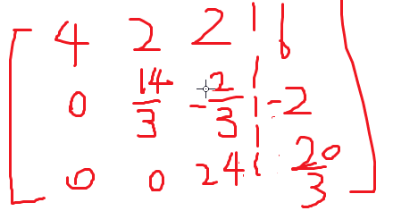
然后搞一搞就行
注意判断无解和无穷解的情况
线性基常见问题:
如何求一堆数的异或和中第 K 大的值?
筛法
常见的埃拉托斯特尼筛,复杂度为 O(nlogn),优化后达到O(nlognlogn)

欧拉筛
让每个合数被他的最小的质因子筛掉

欧拉筛还可以用来维护一些复杂的函数值
如:逆元、一个数的质因数分解中最大的指数的值
积性函数:对于所有互质的 x 和 y,F(x * y) = F(x) * F(y)
完全积性函数:对于所有 x 和 y ,F(x * y) = F(x) * F(y)
常见的积性函数:
欧拉函数 φ(n) :不超过 n 与 n 互素的数的个数
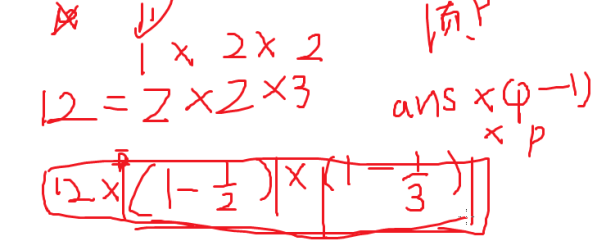
若 
则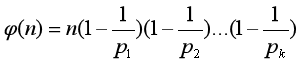
怎么用程序求φ?
欧拉筛,筛数i,选取一个素数p,把p*i筛掉(p<=e[i])
此时会检查i的最小素数因子是不是p
所以会有两种可能
1.i和p互素
Phi[i*p]=phi[i]*phi[p]
2.i的最小素因子刚好是p
Phi[i*p]=phi[i]*p
φ[i]=(p1-1)*p1^(q1-1)+(p2-1)*p2^(q2-1)......(pn-1)*pn^(qn-1)


对于莫比乌斯函数也是差不多
- i和p互素 mul[i*p]=mul[i]*(-1)
- i的最小素因子刚好是p mul[i*p]=0
约数个数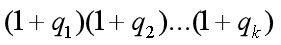
约数和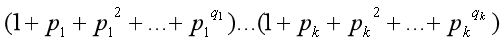
求f(n)=[n/1]+[n/2]+---+[n/n]的值
- k<sqrt(n)的时候,k只有sqrt(n)种取值
所以n div k的取值最多只有sqrt(n)种
div是整除
2.k>sqrt(n)的时候
n div k 显然小于sqrt(n)
所以它的取值也只有sqrt(n)种
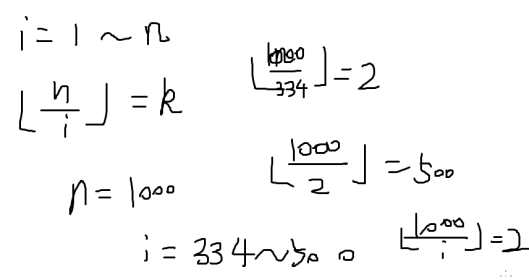
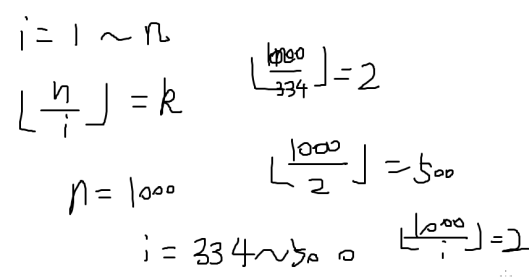
表面上复杂度是o(n),但是由于我们是跳着走的,所以复杂度为o(2√n)