基础算法
枚举
1.输出1~5的所有排列
法一:next_permutation
法二:dfs
2.输出1~n的所有子集的子集
一共有\(3^n\)个
为什么?
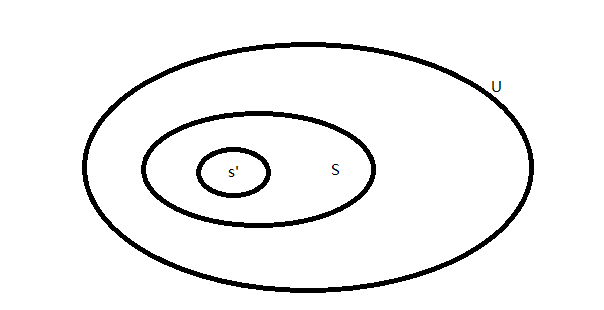
U是全集,S是子集,s'是子集的子集
每个元素有3种可能(在U里面不在S里,在S里不在s'里,在s'里)
每次枚举,都是在判断这n个元素分别在什么位置。一个元素有3种位置,那么总的组合就是\(3^ n\)个
代码怎么写?
暴力思路:第一层枚举子集,第二层枚举集合进行\(check\) 复杂度:\(O(4^n)\)
显然每次枚举再check会浪费时间
怎么\(O(3^n)\)解决这个问题?
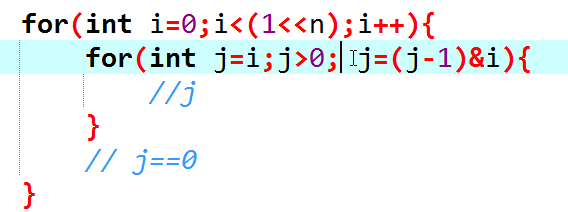
感性李姐每次-1就是生成比当前子集小的最大的集合,与当前枚举的第一层子集取交集
搜索


皇后可攻击她所在的行、列、对角线
我们可以记录当前已经摆了多少个皇后,每次枚举当前行的所有格子,找到合法的格子,并标记当前列、对角线有没有被占用。

从信息比较多的行/列开始搜(按信息量进行sort)

适合解最优解问题(当然,要考虑内存的想法)

用二进制表示是否有某个漏洞,利用bfs进行扩展

一步可以推这个小方块一下(小方块可以倒下,也可以立着),问最少几步把它推进洞里
记录当前的位置,是立着还是倒着,枚举每次操作(推到,立起来,周围的方向)
剪枝常用:可行性剪枝(接下来不可能有解就返回),最优性剪枝(后面的状态最理想的也不会比当前搜到的解优就返回),其中最优性剪枝有些依赖搜索顺序。
经典题:生日蛋糕
蛋糕体积固定为\(N\),层数固定为\(M\),要求下面层的蛋糕半径比上面层大,高度比上面层大,求最小表面积(下地面除外)
肯定是搜索辣
那么是从下到上搜还是从上到下搜呢?
当然是从下到上辣。因为从上到下可能填不满这个\(N\),而从下到上就不会
要记录什么呢? 当前是第几层(从下到上数),体积,半径,高度。当前贡献的侧面积(因为顶面从上面看就和最底下的那层的底面积是一样的).前4个用来搜索,侧面积用来更新答案。
搜完第\(M\)层时,如果体积为\(N\),则更新答案,否则返回。
我们确定底层的时候要枚举\(R\)和\(H\),由于最后体积是\(N\),所以枚举到\(\sqrt n\)就ok了
但是这样会\(TLE\),所以考虑剪枝
可行性剪枝:
我们可以估计一下当前状态如果填完的最小体积,最大体积,如果\(N\)不在这个区间内,则当前状态无解。
最小肯定是第一层是1$\times$1,第二层是\(2 \times 2\)......依次类推。最大体积:从当前层往上\(R\)依次-1,计算体积。当然为了复杂度也可以进行估算,预处理等乱七八糟操作
最优性剪枝:当前侧面积+理论最小侧面积+底面积>ans就直接return (最优化剪枝一般都很强)
代码from zrt
#include<cstdio>
#include<algorithm>
using namespace std;
int n,m;
int ans;
int small[25];
int small_q[25];
void dfs(int x,int v,int q, int R,int H){
// 已经考虑完成最下面x层
// 第x层 R,H
// 当前蛋糕体积为v
if(v>n) return;
if(x==m){
if(v==n){
ans = min(ans,q);
}
return ;
}
if(v + small[m-x] > n) return;
if(q + small_q[m-x] >= ans) return;
int big = v;
for(int i=1;i<=m-x;i++){
big += (R-i)*(R-i)*(H-i);
}
if(big<n) return;
// x+1
for(int i=m-x;i<R;i++){
for(int j=m-x;j<H;j++){
dfs(x+1, i*i*j+v, 2*i*j+q,i,j);
}
}
}
int main(){
http://poj.org/problem?id=1011&lang=zh-CN
ans = 1e9;
scanf("%d%d",&n,&m);
for(int i=1;i<=20;i++){
small[i] = small[i-1] + i*i*i;
small_q[i] = small_q[i-1]+2*i*i;
}
// 最底一层
for(int i=1;i<=n;i++){
if(i*i>n) break;
for(int j=1;j<=n;j++){
dfs(1,i*i*j, 2*i*j + i*i,i,j);
}
}
if(ans == int(1e9)) puts("0");
else{
printf("%d\n",ans);
}
return 0;
}扩展
\(A^*,IDA^*\)
就是一层一层的进行dfs(为了解决bfs容易爆空间以及dfs容易TLE而创造的结合产物)
分治
常见算法:归并排序,快速幂,二分查找/二分答案
就是把序列先拆开再合并
当然它比快排稳定
用途:卡sort时自己写,求逆序对(我只会树状数组.jpg)
写法不怎么常见的快速幂

ex:快(gui)速乘
用途:防止直接乘爆longlong
原理:\(a\times n=n个a\)相加
把快速幂中的乘换成加即可

暴力:每次\(O(n)\)扫一遍
优雅一点:排序之后爆扫
再优雅一点:排序之后二分
二分实数:
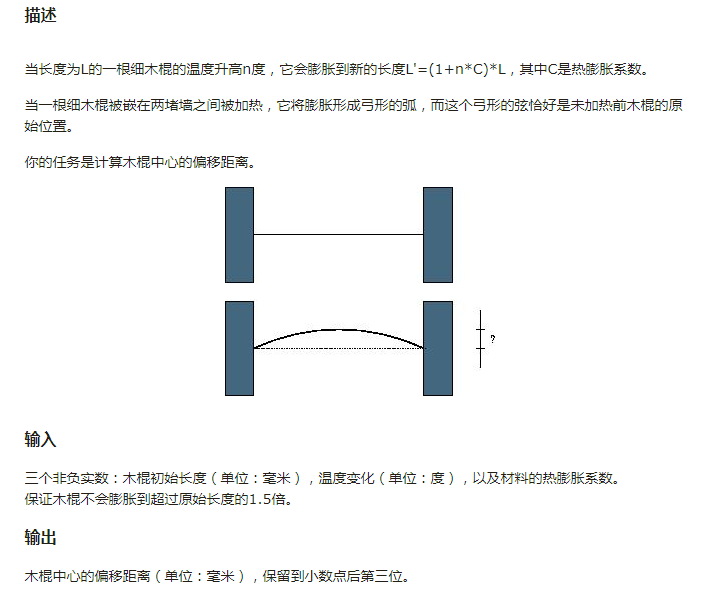
解法一:解方程
设半径为\(r\),圆心角的一半为\(\alpha\)。\(L=2r\ sin\alpha,L'=2\alpha r,L'=(1+n\times c)\times L\)。可以解出来但是我不会
解法二:二分
设偏心距为\(l\),上面的式子整理之后发现\((1+nc)sin\ \alpha=\alpha,l=\frac{L(1-cos\ \alpha)}{2sin\ \alpha}\)
因此,我们可以二分角度来搞
贪心
有一堆怪,打第\(i\)只会掉\(d_i\)滴血,加\(a_i\)滴血,求最多打几只怪
肯定是个贪心,但是按什么排序呢?
当\(a_i\geq d_i\)时,肯定按\(d_i\)从小到大打
当\(a_i<d_i\)时,怎么打呢?
1.按\(d-a\)从小到大
2.按\(d\)从小到大
3.按\(d\)从大到小
4.按\(a\)从小到大
5.按\(a\)从大到小
正确方法是5
5为什么是对的?
先来张图李姐李姐

这是打前半段时的血量的变化
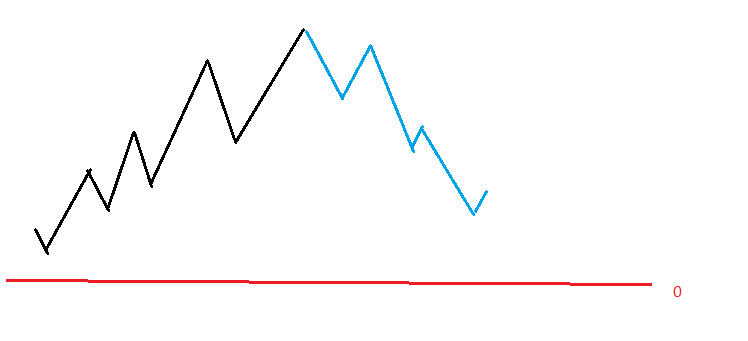
这是理想状态下的血线变化,当血量降到0线以下就死亡。
我们发现这两半几乎是对称的,那么如果倒着看第二段,即把\(a\)(回血)看成\(d\)(扣血),把\(d\)看成\(a\),那么这时回血>扣血,就和第一段一样了。再正回来,就是按\(a\)从大到小排。
其他几个选项的hack:
按\(d-a\):血量:100 \(d_1=98,a_1=96,d_2=96,a_2=94\)
按\(d\)从小到大:同上
按\(d\)从大到小:血量:100,\(d_1=98,a_1=1,d_2=97,a_2=96\)
按\(a\)从小到大:显然反了
数组
前缀和与差分
实现区间修改

栈:一般用数组模拟
应用:dfs,表达式求值
表达式求值
重点是运算的优先级
开两个栈,一个存数字,另一个存运算符号
要保证符号栈中的符号优先级不递减(如果出现要递减的情况就运算)
如果没有括号,就保证符号栈中乘号在加/减号上面。如果在一堆乘号之后出现了加号,则先运算这一堆乘号。
那么有括号了怎么处理呢?左括号相当于分隔符,左括号之后(右括号之前)的符号的维护与之前的符号的优先级维护互不干扰,左括号内部就像上面一样维护。出现右括号就立刻弹栈,运算括号。
有一点要注意,我们计算的时候一般是从左往右算,所以即使是同级都要计算,例如5-3-2,如果一直屯着减号就会先算3-2,再算5-1,就会wa
右结合:乘方
单调栈&单调队列
单调栈:


poj P2559
所有矩形宽度为1,高度由输入给出,求最大子矩形的面积。
最最暴力的方法是枚举\(l,r\)。复杂度\(O(n^2)\)
优化:我们可以先固定一个点,寻找另一个点的规律。我们发现如果高度是上升的,那么宽度就可以扩展,不需要管。如果高度下降了,那么就有可能宽度无法继续扩展。如果宽度无法继续扩展,则算一下之前的答案,否则即使是高度降低了也不进行计算。
这样我们可以维护高度递增的栈。栈内维护二元组,记录矩形高度和款。如果有低的高度要入栈,则砍掉之前没有用的高度,进行计算。降高度的时候,可以先算一下原本的高度能造出的矩形,再降高度计算矩形面积,更新答案。当遇到一个比要入栈的高度还要小的高度时,停止弹栈,将这个高度与之前计算累计下来的宽度入栈。
单调队列
一般使用stl中的queue进行模拟
用途:

经典题:滑动窗口
好了我们来看看单调队列
维护当前最小(大)值对应的下标,如果这个下标“过时”了,就pop。以求最小值为例,如果当前数比前面的数小,就一直从队尾pop前面的数。最大值同理
当然也可以在求最大值时把序列的所有数都乘-1,求最小值
二叉搜索树
满二叉树:全满了
完全二叉树:最后一层的孩子可以少几个,但是少的必须是连续的。
二叉搜索树:中序遍历(左、中、右)得到的序列有序(一般是某个节点的左子树都比他小,右子树都比他大。
支持插入,查找大于/小于某个数的数,但是复杂度及其之不优美(依赖插入顺序)。因为插入的顺序可以把树高变成\(O(n)\)。可以用平衡树来优化
因为复杂度太劣了所以貌似真没什么应用。
RMQ问题
给一个序列,问区间最大/最小值
ST表
可处理没有修改的区间查询
如果我们不会ST表怎么办?暴力,线段树,莫队
好我们回到正题
我们先来看看区间求最大值和区间求和的区别。
区间最大值:不断取最大,不支持减法,可以重叠
区间求和:前缀和,支持减法,如果有重叠要处理重叠
ST表要处理一些区间,来使这些区间可以覆盖任意一个区间。
那么处理哪些区间呢?
利用区间倍增处理处\([l,l+2^i]\)这段区间的最大值。对于每个\(l\),都有\(log\ n\)个区间要处理,所以总复杂度是\(O(nlongn)\)
如何覆盖?
设当前区间长度为\(len\),左端点为\(l\),右端点为\(r\).一定可以找到一个\(k\),使得\(2^k \leq len <2^{k+1}\)。找\([ll,l+2^k],[r-2^k,r]\)来覆盖这个区间。
一般设\(st[i][j]\)表示区间\([l,l+2^j]\)中的最大值。
\(st[i][j]=max\{[i][j-1],st[i+(1<<(j-1))][j-1]\}\)。在覆盖的时候,我们可以算出\(log_2{len}\)来知道\(k\)。由于\(c++\)自带的函数太慢了,所以我们进行预处理。
覆盖:

二维ST表
二维区间和是用二维前缀和加加减减求得,但是求最大值不支持减法,所以我们处理每个点向右\(2^i\),向下\(2^j\)的最大值,用4个相同的小块来覆盖要求的部分
与倍增\(lca\)的一点联系:处理\(fa[x][i]\):\(fa[x][i]=fa[fa[x][i-1]][i-1]\)
求欧拉序:
欧拉序:每经过一个点,就记录一下
炒个栗子:
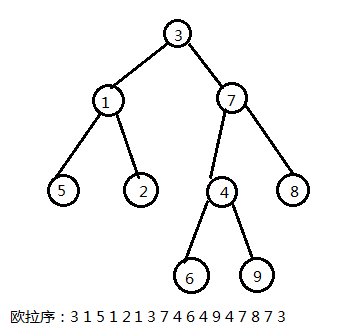
长度:\(2^n-1\)
把他们的深度记下来:
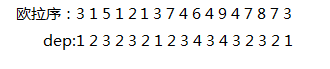
深度似乎和\(lca\)有点联系
一段区间里深度最小的点是这一坨点的\(lca\)
我怕不是学了假的欧拉序
可以再用ST表记录取到最小值的位置,然后就可以找到\(lca\)了。
因为这里每次深度要么+1,要么-1,所以也叫±1\(RMQ\)
有许多种欧拉序,这只是其中的一种
并查集
支持:合并集合,查询两个集合是否在同一集合中
按秩合并:
记录一个\(siz\)表示集合的大小,由小的集合连向大的集合比大的连小的要更优(有更少的元素找根需要多走一条边)。

初始的\(siz\)是个随机数\(pwq\)
路径压缩:查询的时候直接把父节点,祖父节点,曾祖父节点......直接接到根上
启发式合并:

显然把小的数组塞到大数组里面要好一些。每次合并之后的大小是原来的小集合大小的2倍以上。这样看,最多合并\(log\ n\)次,每次合并是\(O(n)\)的,所以总复杂度是\(O(nlogn)\)