最短路径 —— Dijkstra 算法和 Floyd 算法

Dijkstra 算法

目的： 求某一顶点到其余各顶点的最短路径，其 算法复杂度O(n^2)

算法思想： 设有两个顶点集合 S 和 U，集合 S 中存放图中已找到最短路径的顶点，集合 U 存放图中剩余顶点。初始状态时，集合 S 中只包含源点 v0，然后不断从集合 U 中选取到顶点 $v_0$ 路径长度最短的顶点 $v_u$ 并入集合 S 中。集合 S 每并入一个新的顶点 $v_u$ ，都要修改顶点 $v_0$ 到集合 U 中顶点的最短路径长度值。不断重复此过程，直到集合T的顶点全部并入S中为止。

若以每一个顶点为源点，重复执行Dijkstra算法n次，即可求出每一对顶点之间的最短路径。此时，算法复杂度为O(n^3)

若要使用代码实现 Dijkstra 算法，可定义以下数组

• $dist[v_i]$：表示当前已找到的从v0到每个终点vi的最短路径的长度。dist[ ]的初态为：若从v0到vi有边，则dist[vi]为边上的权值，否则置dist[vi]为∞

• $path[v_i]$：中保存从v0到vi最短路径上vi的前一个顶点，假设最短路径上的顶点序列为 $v_0，v_1，...，v_i$，则 path[vi]=v(i-1)。path[ ]的初态为：如果 $v_0$ 到 $v_i$ 有边，则 path[vi]=v0，否则 path[vi]=-1

• $set[v_i]$：为标记数组，set[vi]=0表示vi在集合U中，即没有被并入最短路径；set[vi]=1表示vi在集合S中，即已经并入最短路径。set[ ]的初态为：set[v0]=1，其余元素全为0

算法过程

---

Floyd 算法

目的： 每一对顶点之间的最短路径，其 算法复杂度O(n^3)

算法思想： 假设dist(i,j)为节点u到节点v的最短路径的距离，对于每一个节点k，我们检查dist(i,k) + dist(k,j) < dist(i,j)是否成立，如果成立，证明从i到k再到j的路径比i直接到j的路径短，我们便设置dist(i,j) = dist(i,k) + dist(k,j)，这样一来，当我们遍历完所有节点k，dist(i,j)中记录的便是i到j的最短路径的距离。

算法过程

初始化

给出矩阵，其中矩阵 D 是邻接矩阵，而矩阵 Path 记录 u,v 两点之间最短路径所必须经过的点

$D_{-1}= \left\{ \begin{matrix} 0 &amp; 1 &amp;∞ &amp; 4\\ ∞ &amp; 0 &amp; 9 &amp; 2\\ 3 &amp; 5 &amp; 0 &amp; 8 \\ ∞ &amp; ∞ &amp; 6 &amp; 0 \end{matrix} \right\} Path_{-1}= \left\{ \begin{matrix} -1 &amp; -1 &amp; -1 &amp; -1 \\ -1 &amp; -1 &amp; -1 &amp; -1\\ -1 &amp; -1 &amp; -1 &amp; -1 \\ -1 &amp; -1 &amp; -1 &amp; -1 \end{matrix} \right\}$

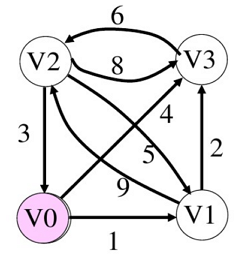
第一步

D[2][1]=D[2][0]+D[0][1]=3+1=4
D[2][3]=D[2][0]+D[0][3]=3+4=7

第二步

第三步

第四步