轨迹规划

目的

　　本文介绍机器人单关节轨迹规划中常用的几种方式。

1　多项式

　　多项式是最简单的函数了，一般用五次多项式表示一段轨迹 $^{[1]}$ ，因为它刚好有6个系数，而我们的边界条件也是6个：起点和终点的位置 $s_{0}$ 、 $s_{T}$ ，起点和终点的速度 $\dot{s}_{0}$ 、 $\dot{s}_{T}$ ，再加上起点和终点的加速度 $\ddot{s}_{0}$ 、 $\ddot{s}_{T}$ 。
$s\left( t\right)= c1 t^{5}+c2 t^{4}+c3 t^{3}+c4 t^{2}+c5 t+c6$
　　通过求解这组线性方程就可以得到6个系数。
$\left( \begin{array}{l}{s_{0}} \\ {s_{T}} \\ {\dot{s}_{0}} \\ {\dot{s}_{T}} \\ {\ddot{s}_{0}} \\ {\ddot{s}_{T}} \end{array}\right)=\left( \begin{array}{cccccc}{0} & {0} & {0} & {0} & {0} & {1} \\ {T^{5}} & {T^{4}} & {T^{3}} & {T^{2}} & {T} & {1} \\ {0} & {0} & {0} & {0} & {1} & {0} \\ {5 T^{4}} & {4 T^{3}} & {3 T^{2}} & {2 T} & {1} & {0}\\ {0} & {0} & {0} & {2} & {0} & {0} \\ {20 T^{3}} & {12 T^{2}} & {6 T} & {2} & {0} & {0}\end{array}\right) \left( \begin{array}{l}{c1} \\ {c2} \\ {c3} \\ {c4} \\ {c5} \\ {c6}\end{array}\right)$
　　我们可以调整边界条件来观察曲线的形状，如下图。可见位置、速度、加速度、加加速度（Jerk）都是连续而且光滑的，这意味着机器人或者机床等机构在运动时比较平滑、不会有冲击。由此可见，多项式函数比较适合表示一段轨迹。

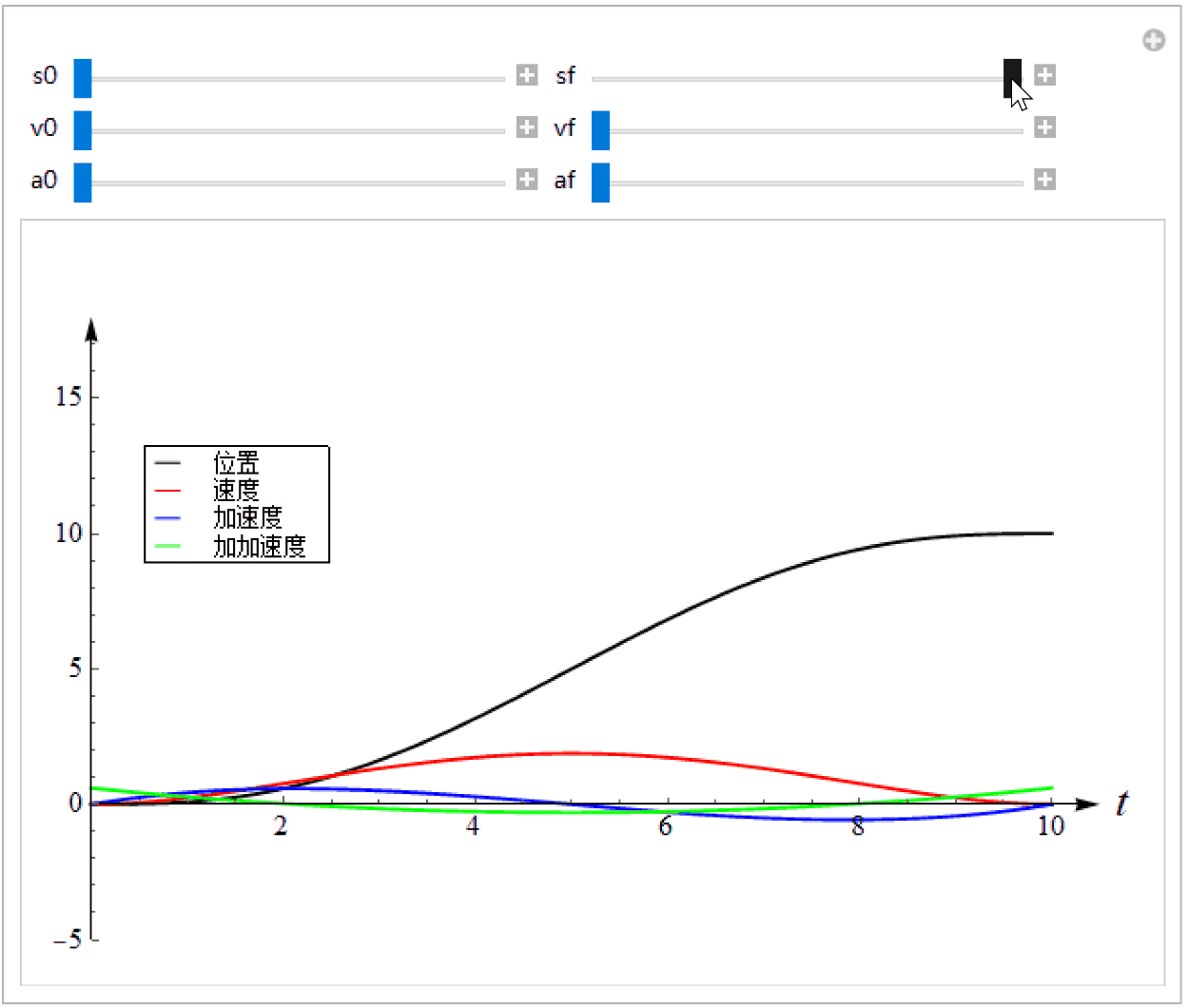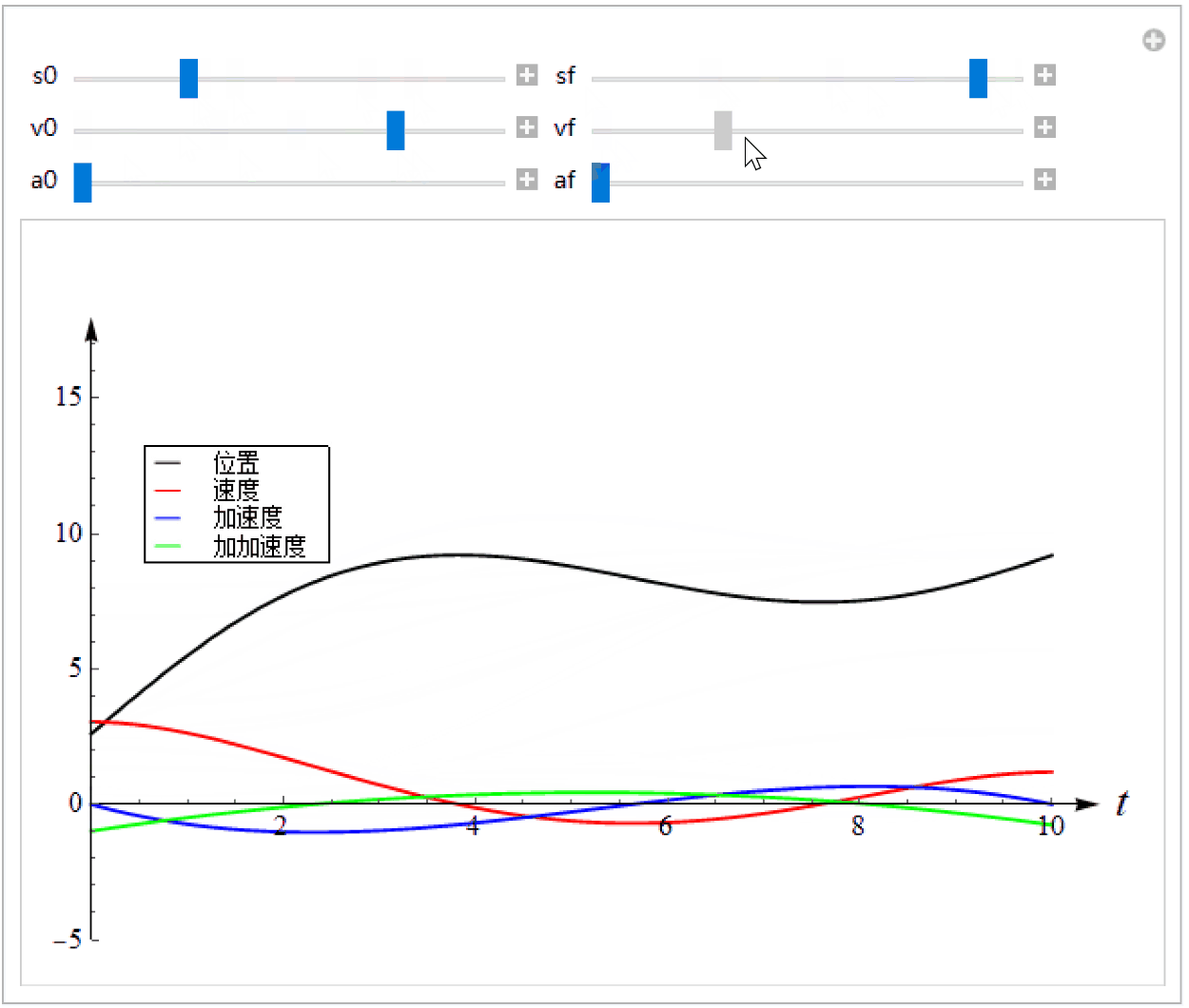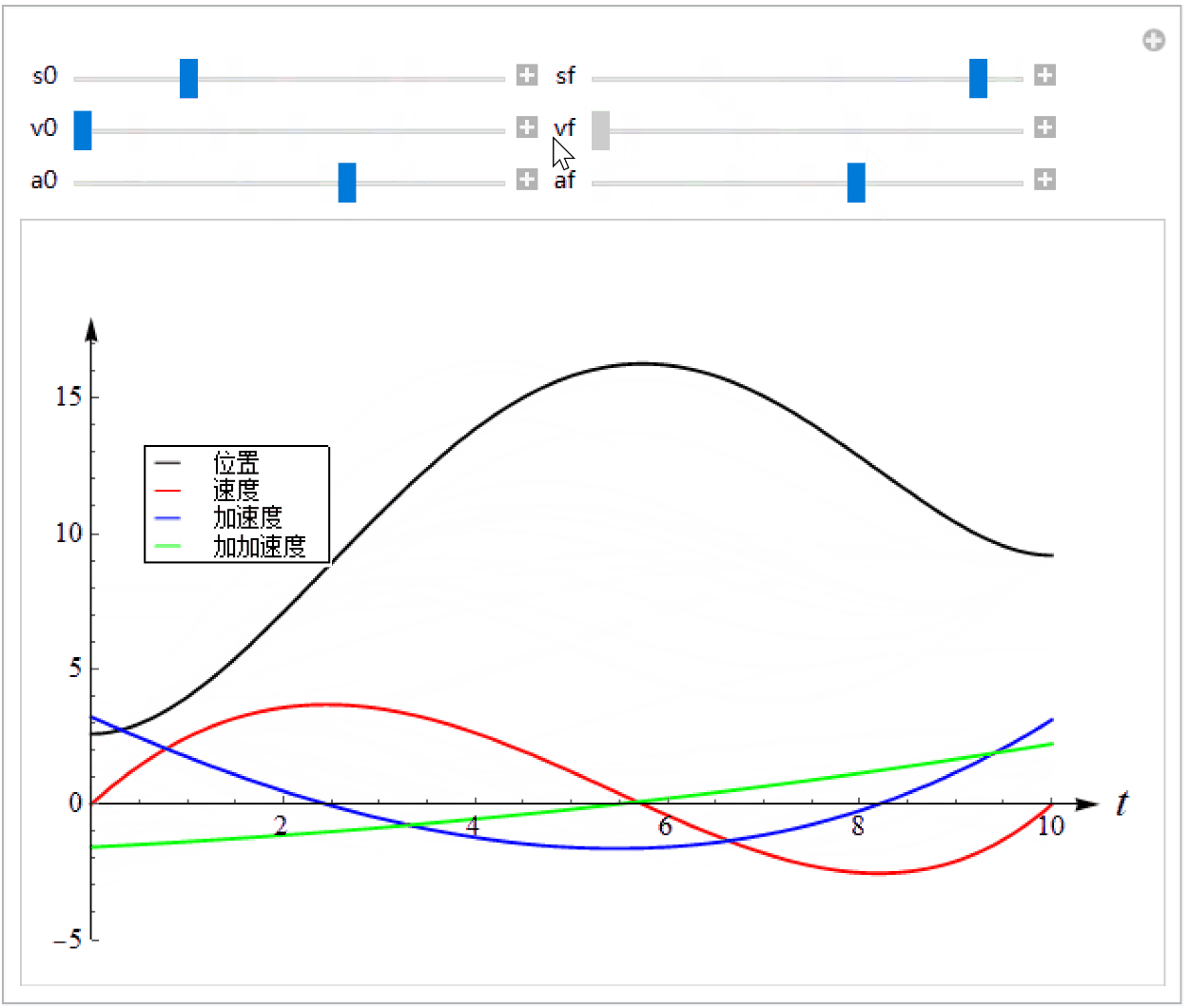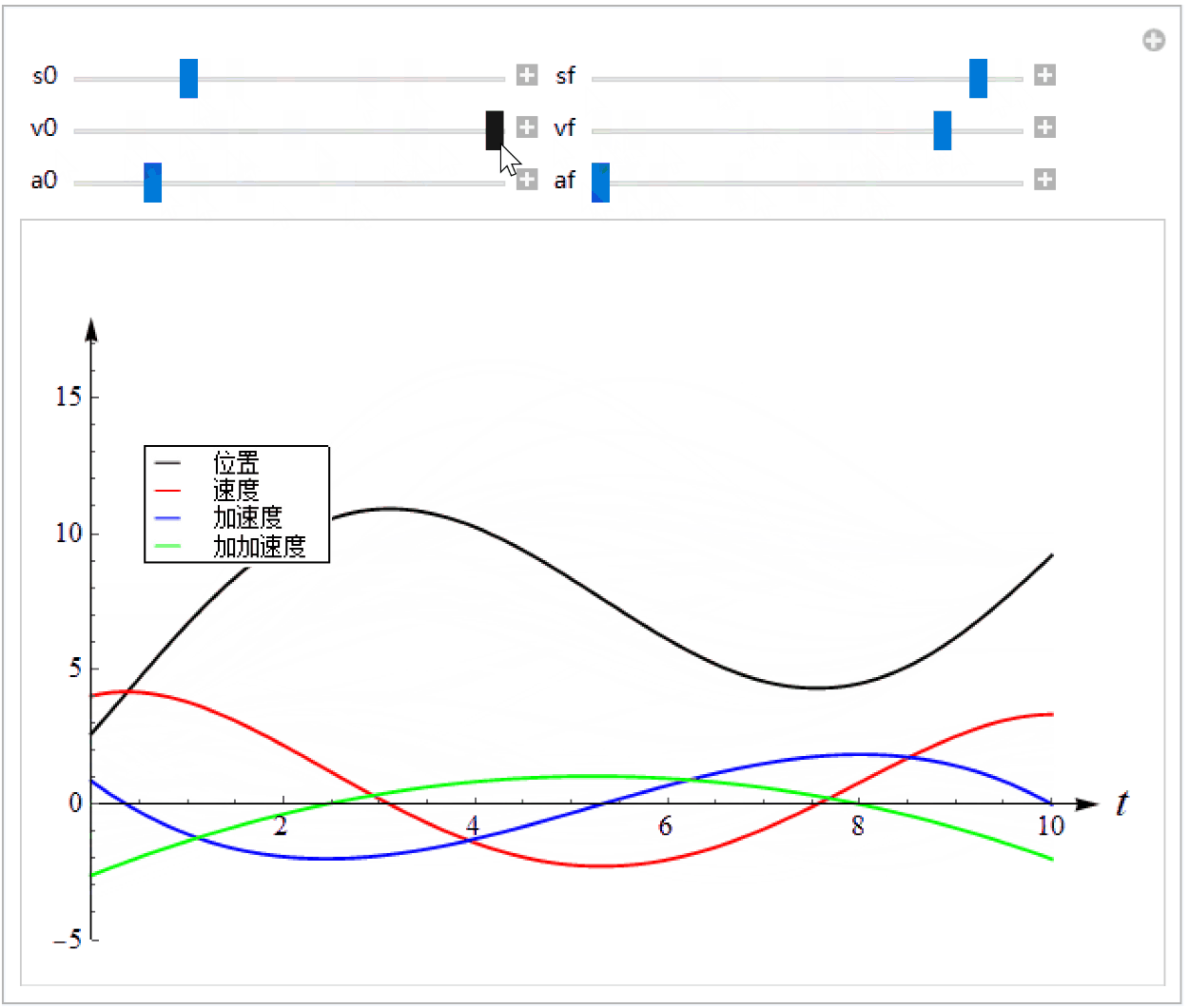
T = 10.0;
A = {{0 , 0, 0 , 0 , 0 , 1},
     {T^5, T^4, T^3, T^2, T , 1},
     {0, 0, 0, 0, 1, 0},
     { 5*T^4, 4*T^3, 3*T^2, 2*T, 1, 0},
     {0 , 0, 0, 2, 0, 0 }, 
     {20*T^3, 12*T^2 , 6*T, 2, 0 , 0}};
Manipulate[
 Y = {s0, sf, v0, vf, a0, af};
 Quiet[c = Inverse[A].Y];
 s[x_] := {x^5, x^4, x^3, x^2, x, 1}.c;
 vel[y_] = D[s[y], y];
 acc[y_] = D[vel[y], y];
 jerk[y_] = D[acc[y], y];
 Plot[{s[x], vel[x], acc[x], jerk[x]}, {x, 0, T}, PlotStyle -> {Black, Red, Blue, Green}, PlotRange -> {{0, 10}, {-5, 18}}],
 Grid[{{Control[{{s0, 0}, 0, 10, 0.01}], Control[{{sf, 10}, 0, 10, 0.01}]}, {Control[{{v0, 0}, 0, 4, 0.01}], Control[{{vf, 0}, 0, 4, 0.01}]}, {Control[{{a0, 0}, 0, 5, 0.01}], Control[{{af, 0}, 0, 5, 0.01}]}}], TrackedSymbols :> True]

　　物体在时域中的实际运动如下图所示。

Animate[Graphics[{Ball[{s[t], 0}, 0.2]}, PlotRange -> {{-1, 11}, {-1, 1}}], {t, 0, 10, 0.1}]

2　梯形速度曲线

　　多项式的优点是实现简单，但是缺点是大部分时间速度比较小，性能没有充分发挥，运动效率低。一种改进方法是利用分段多项式，此时速度为梯形，又称为梯形速度曲线。

Manipulate[
 T = 10.0;
 tb = (s0 - sf + V*T)/V;
 a = V/tb;
 s[t_] := Piecewise[{{s0 + a/2*t^2, t < tb}, {(sf + s0 - V*T)/2 + V*t, tb <= t < T - tb}, {sf - a/2*T^2 + a*T*t - a/2*t^2, T - tb <= t}}];
 vel[t_] := Piecewise[{{a*t, t < tb}, {V, tb <= t < T - tb}, {a*(T - t),  T - tb <= t}}];
 acc[t_] := Piecewise[{{a, t < tb}, {0, tb <= t < T - tb}, {-a, T - tb <= t}}];
 Plot[{s[t], vel[t], acc[t]}, {t, 0, T}, PlotStyle -> {Black, Red, Blue}, PlotRange -> {{0, 10}, {-5, 11}}], Grid[{{Control[{s0, 0, 10, 0.01}],  Control[{{sf, 10}, 0, 10, 0.01}]}, {Control[{{V, 1.5}, 1.02, 2,   0.01}]}}], TrackedSymbols :> True]

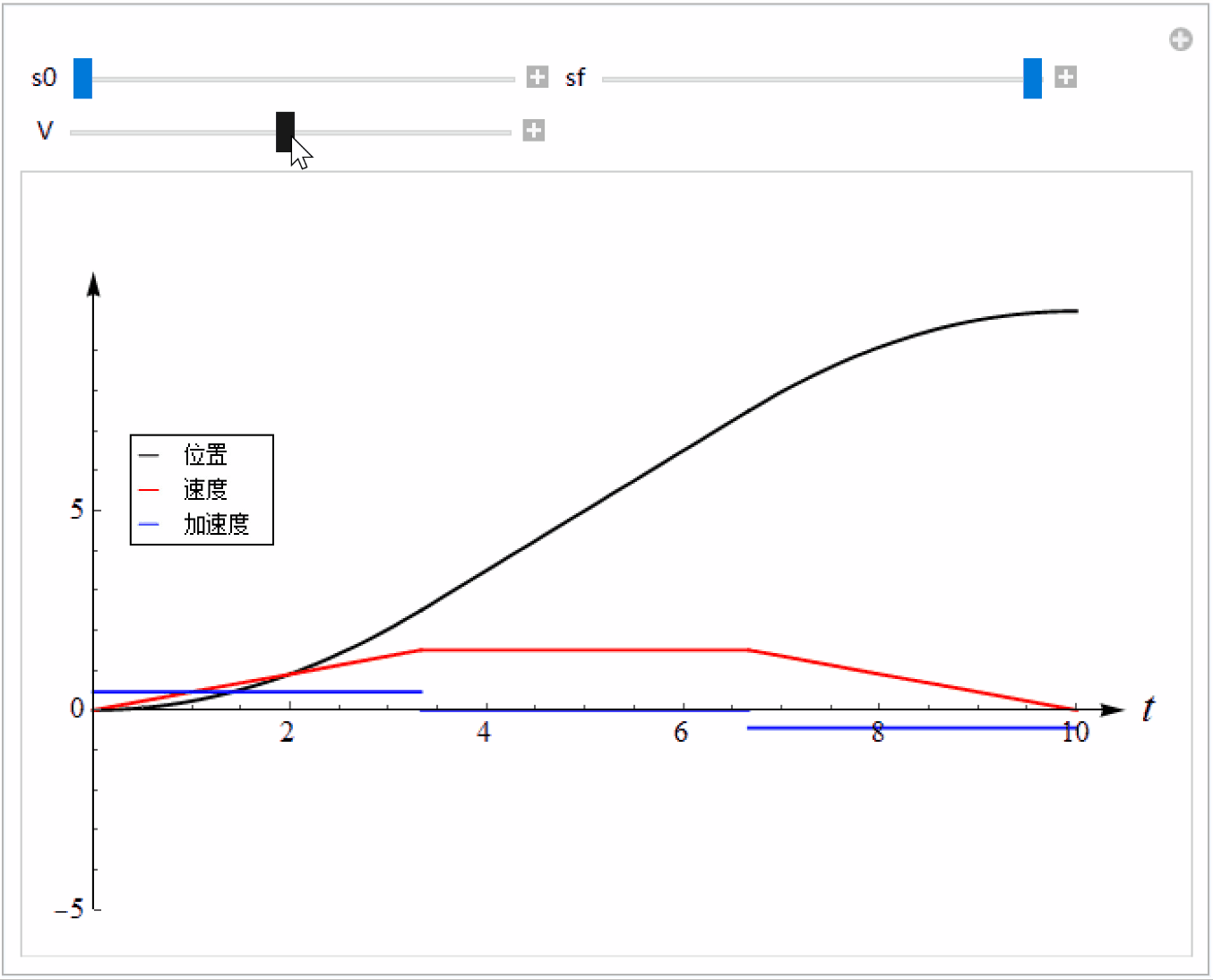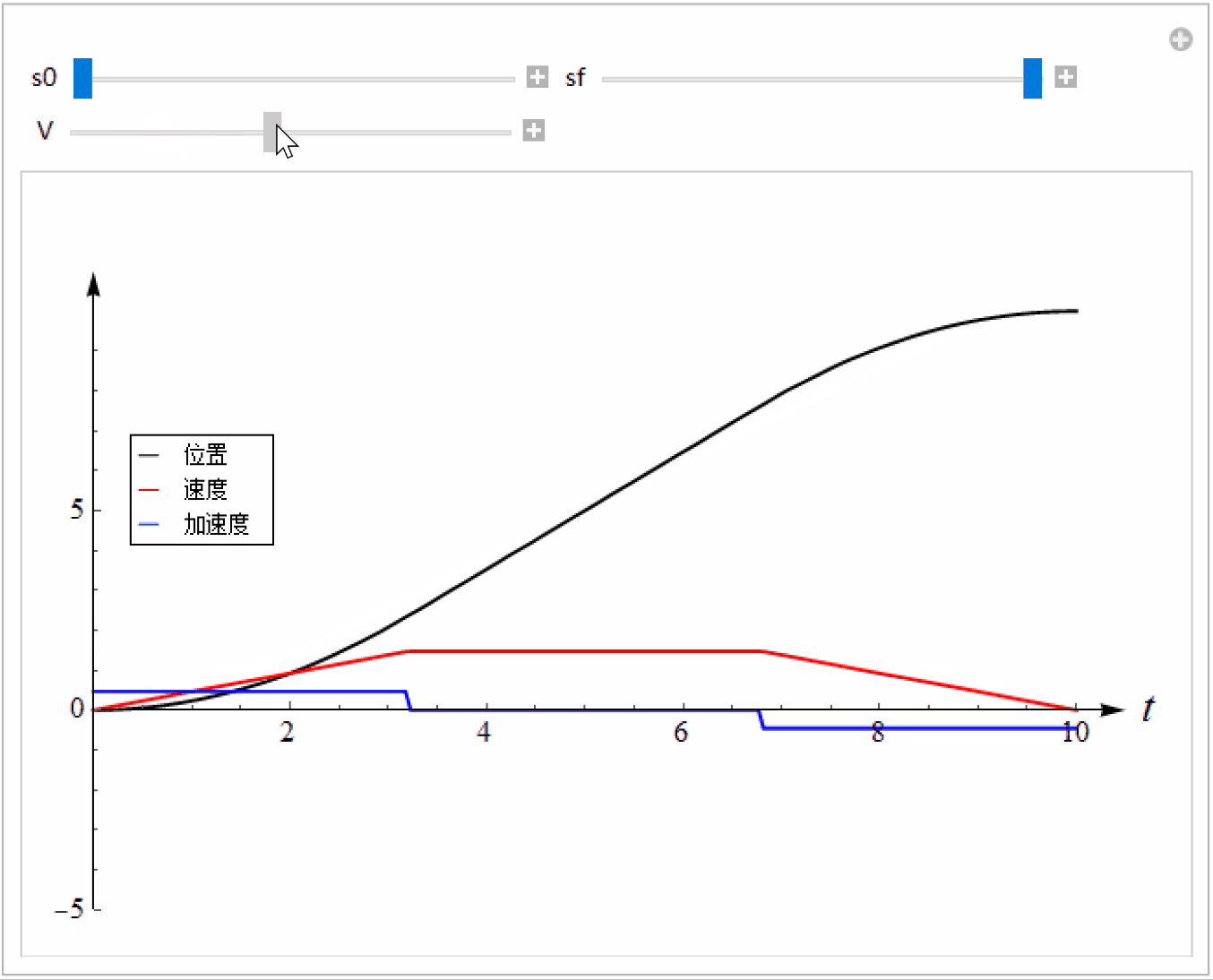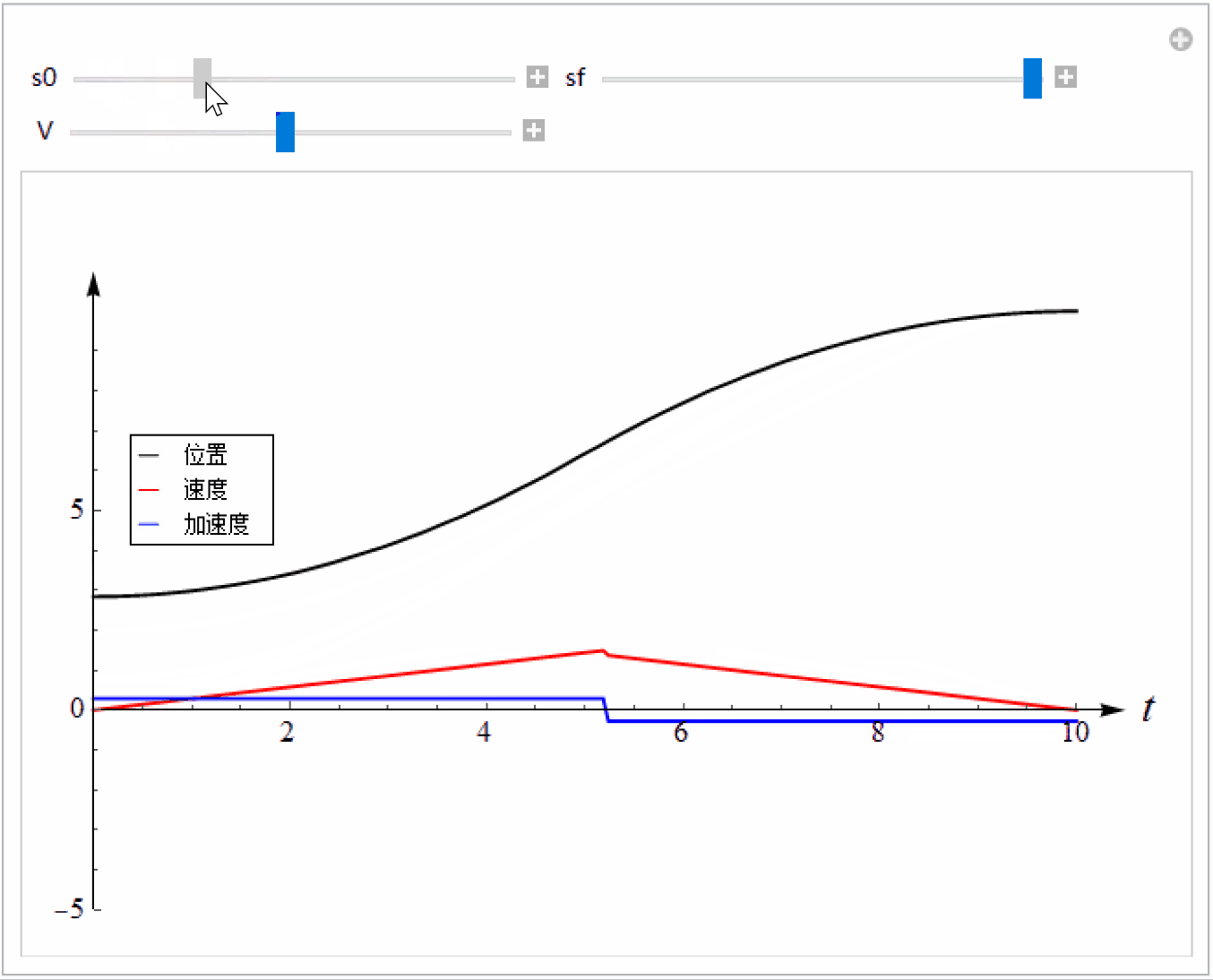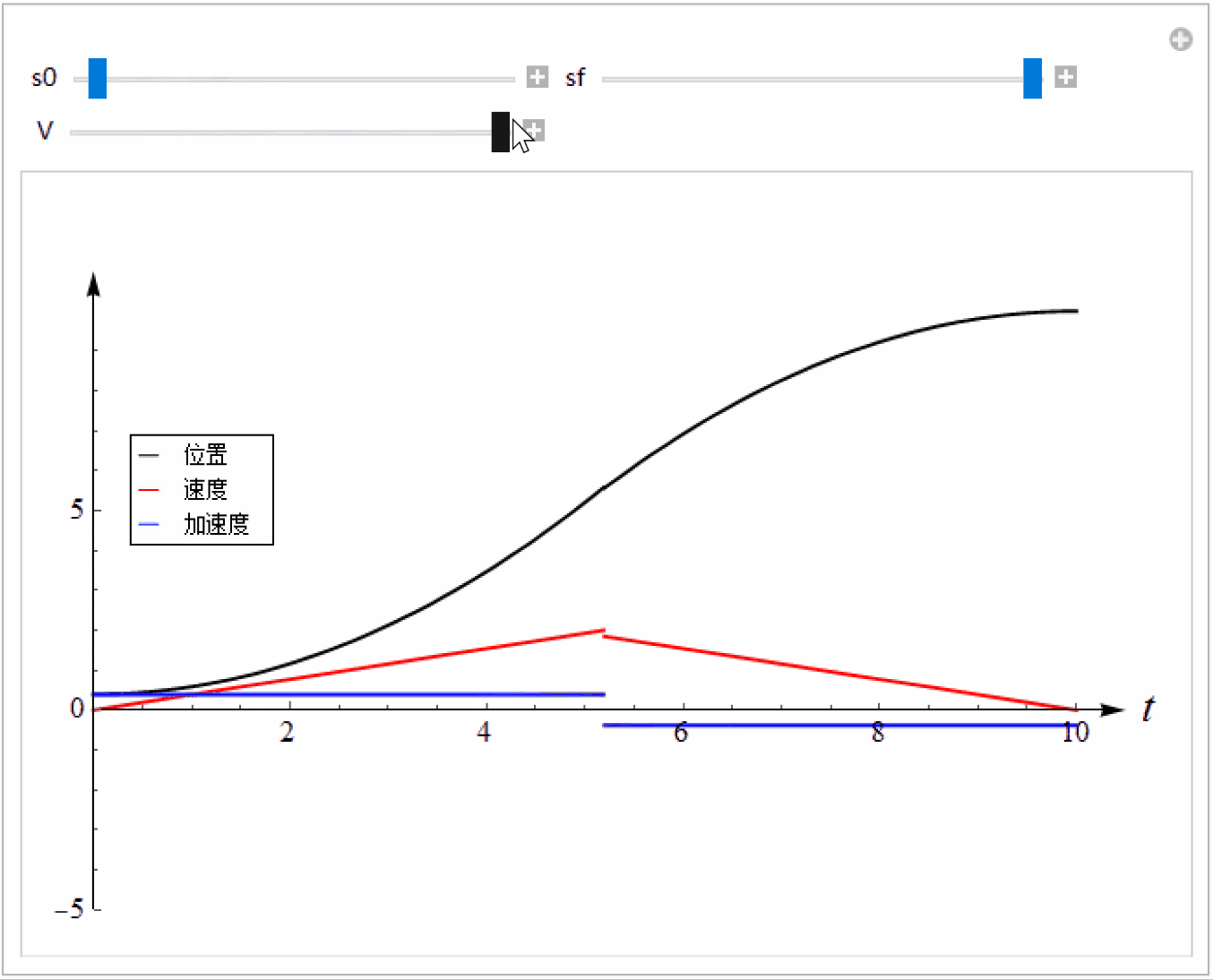
3　 $\textrm{s}$ 形曲线

　　梯形速度曲线的优点是可以在一段比较长的时间保持较大的速度，缺点是加速度不连续，加加速度在切换点的值是无穷大，这在实际应用中会造成冲击，容易造成机械设备损坏。我们可以让加速度也是连续的，同时尽量保持最大速度。此时加速度的形状是梯形，而速度呈S形，故得名S形速度曲线（S-curve $^{[2]}$ ，也叫双 S 曲线或7段曲线 $^{[2]}$ ）。

3　 $\textrm{super-s}$ 曲线

　　super-s曲线的加加速度是按照正弦曲线变化的 $^{[2]}$ ，如下图中的绿色曲线所示。整个轨迹由7段组成。

扫描二维码关注公众号，回复： 6562565 查看本文章

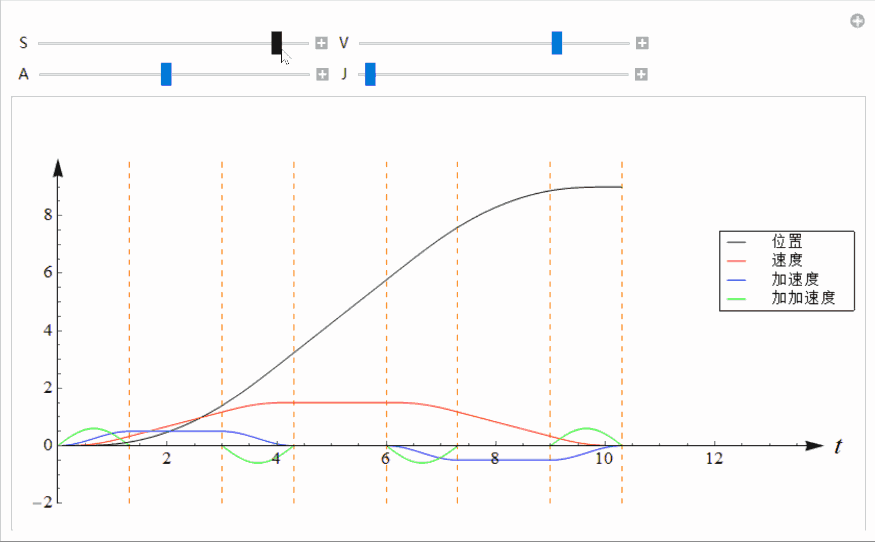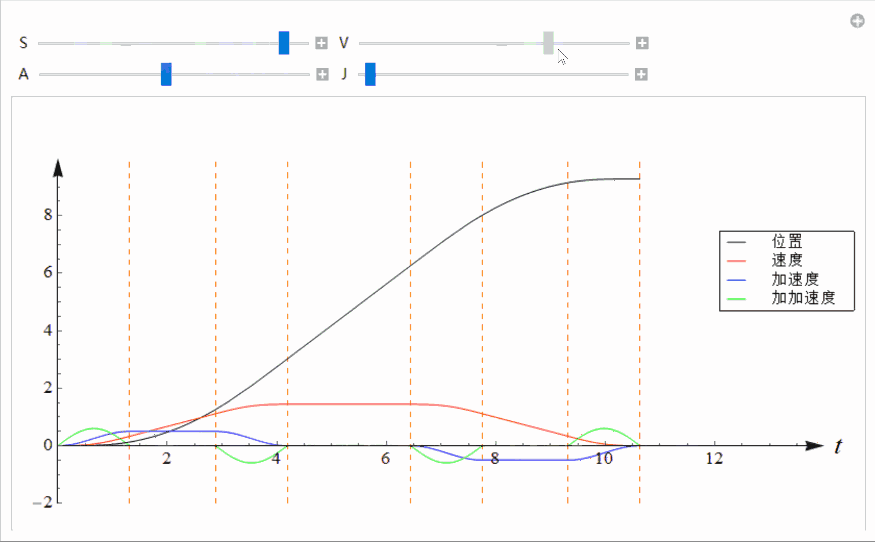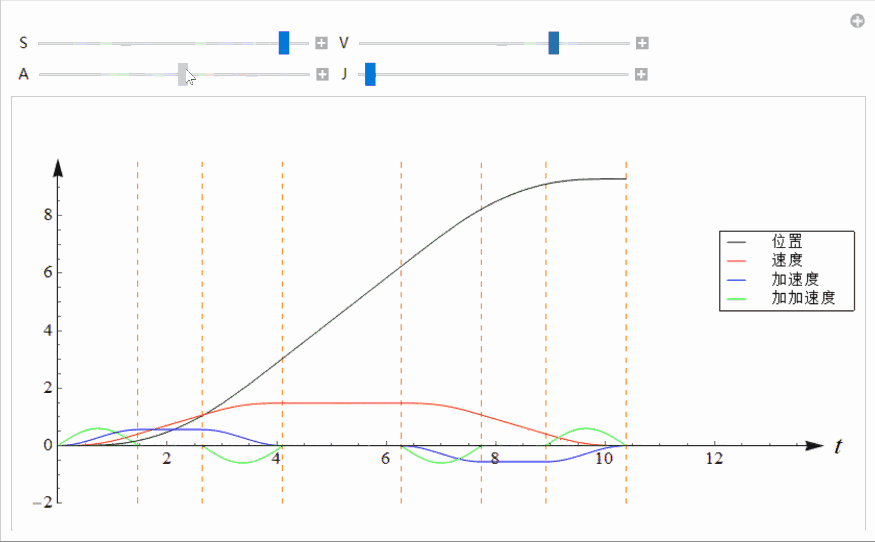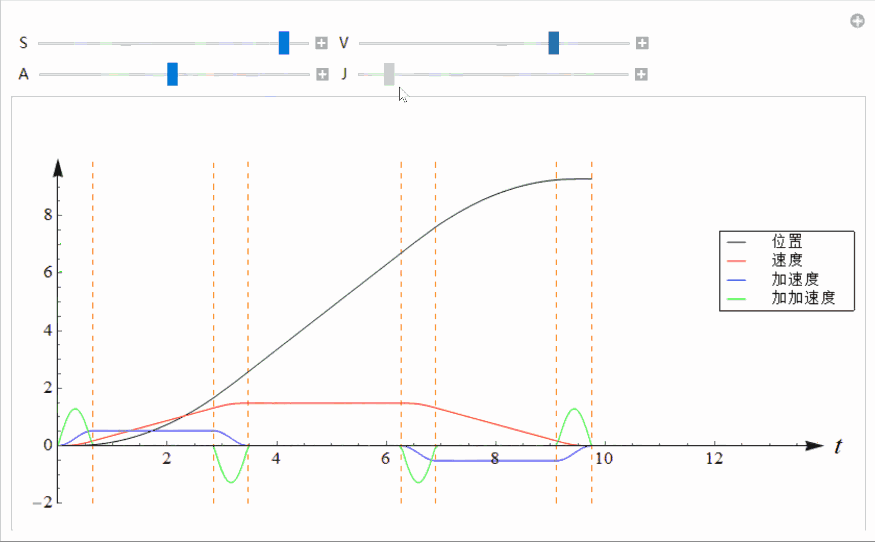
4　 $\textrm{s-}\gamma$ 曲线

　　分段多项式的优点是大速度可以保持一段比较长的时间，缺点是加速度不连续，或者说加加速度在切换点的值是无穷大，这在实际应用中会造成冲击，容易造成机械设备损坏。

5　参考资料
　　　　
[1]　Robotics, vision and control fundamental algorithms in MATLAB，Peter Corke.
[2]　https://github.com/nameofuser1/py-scurveMotion
[3]　Profile Design to Reduce Residual Vibration of High-Speed Positioning Stages，Huaizhong Li，IEEE/ASME TRANSACTIONS ON MECHATRONICS，2009.
[3]　Trajectory Planning for Automatic Machines and Robots-Springer， by Luigi Biagiotti, Claudio Melchiorri，2008.

猜你喜欢