题意:
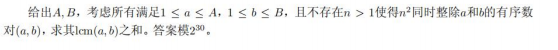
推式子
我们考虑把这个式子的形式转变一下
首先,分别整除可以转变成他们的 \(gcd\) 整除
其次,考虑整除一个平方项,我们可以联想到一个欧拉函数 \(\mu\)
于是,我们要求的式子就变成了
\[ \large \sum_{a=1}^A \sum_{b=1}^B [\mu(gcd(a,b))\neq 0] \frac{a*b}{gcd[a,b]} \]
很明显这里就是一个莫比乌斯反演的式子,然后按照套路把 \(gcd\) 提出来
\[ \large \sum_{\mu(k) \ neq 0 } \frac{1}{k} \sum_{a=1}^A \sum_{b=1}^B [gcd(a,b)==k] \frac{a*b}{gcd[a,b]} \]
\[ \large \sum_{\mu(k) \ neq 0 } k \sum_{a=1}^{\frac{A}{k}} \sum_{b=1}^{\frac{A}{k}} [gcd(a,b)==k] a*b \]
然后接下来的一部分和简单数学题一样,把后面的部分进行莫比乌斯反演,然后带回来,得到
\[ \large Ans=\sum_{\mu(k) \ neq 0 } k \sum_{d=1}^{\frac{A}{k}} \mu(d) S\Big( \Big\lfloor \frac{n}{kd} \Big\rfloor \Big)^2 \]
按照套路 \(T=kd\)
\[ \large Ans=\sum_{T=1}^A S\Big(\Big\lfloor \frac{A}{T} \Big\rfloor \Big)^2 \sum_{d|T \mu(k) \neq 0 } \mu \Big(\frac{T}{d}\Big) \Big(\frac{T}{d}\Big)^2 d \]
到了这一步,我们已经基本上可以做了,打一个简单的 \(nlogn\) 的筛加上整除分块,复杂度就变成了 \(nlogn+T\sqrt{n}\) ,常数优秀一点就可以切掉了,但是我们还有更优秀的线性筛