Large scale machine learning(大规模机器学习)

前言

这一章内容还是紧接着上一章的内容，在前面我们给大家介绍了很大的机器学习方法，如线性回归，逻辑回归，神经网络等，在这一章将给大家介绍下，当我们拥有大量的数据时，该如何运用这些算法，或者说该如何改进，使算法运行更快。

最后，如果有理解不对的地方，希望大家不吝赐教，谢谢！

第十五章 Large scale machine learning(大规模机器学习)

15.1 大量数据的学习

在前面我们有一个例子，就是在容易混淆的单词中选出我们想要的那个单词，比如我们有{two,to,too}，对于For breakfast I ate ___ eggs.我们都知道填two，但是机器在进行学习时，需要根据大量的数据进行学习，所以整个系统规模是比较大的。实际上，在很多机器学习的问题上，我们也是比较喜欢拥有大量的数据的，对于一个好的算法，我们更希望拥有大量的数据，我们要做的是用不怎么好的算法去用大量的数据不断训练得到最好的结果。如图1所示，当数据不断增加时，不同学习算法最后所表现出的效果是相近的，而且可以发现当数据很大时，各个算法的效果越好，这也证实了一个好的学习系统，我们需要大量的数据做支持。

图1 不同算法的准确性和数据规模的关系

不过在前面，我们也有讨论过并不是所有的学习系统通过增加数据就能使训练的效果越好的，所以我们需要用学习曲线来帮我们判断是否需要使用大量的数据。比如对于高偏差的系统，如图2所示，当数据增加到一定程度时，会发现再增加数据并没有很大的效果，所以我们不能增加数据了，而对于高方差的问题，如图3所示，我们就可以通过增加数据来改善系统的效果。

图2 高偏差系统的学习曲线

图3 高方差系统的学习曲线

15.2 随机梯度下降法

我们用线性回归的梯度下降算法来讲解如何根据梯度下降算法演变为随机梯度下降法，要注意下，随机梯度下降算法不仅只适用于线性回归问题，对于逻辑回归，神经网络等都适用。

首先，我们来回顾下线性回归的梯度下降法，对于预测函数我们有 $h_{\theta }(x)=\sum_{j=0}^{n}\theta _{j}x_{j}$ ，代价函数是 $J_{train}(\theta )=\frac{1}{2m}\sum_{i=1}^{m}(h_{\theta }(x^{(i)})-y^{(i)})^2$ ，不断更新 $\theta _{j}:=\theta _{j}-\alpha \frac{1}{m}\sum_{i=1}^{m}(h_{\theta }(x^{(i)})-y^{(i)})x_{j}^{(i)}$ (for every j=0,1,...,n)，对于更新 $\theta _{j}$ ，我们会发现每次更新 $\theta _{j}$ ，我们都要对所有的数据进行求和一次，即需要遍历一次所有的数据，所以当我们有很大的数据时，比如在统计一个地方的人口时，则会有大量的数据，假设m=300,000,000，这个时候我们每次进行更新 $\theta _{j}$ ，我们则会有很大的计算量，而且这只是进行一次更新，我们还需要不断地更新，这样整体的速度就会比较慢，所以我们需要对算法进行改进，这就有了我们的随机梯度下降法。对于传统的梯度算法，我们也有一个名称为批量梯度算法。

对于批量梯度算法的代价函数 $J_{train}(\theta )=\frac{1}{2m}\sum_{i=1}^{m}(h_{\theta }(x^{(i)})-y^{(i)})^2$ ，我们重新定义一个 $cost(\theta ,(x^{(i)},y^{(i)}))=\frac{1}{2}(h_{\theta }(x^{(i)})-y^{(i)})^2$ ，这个时候 $J_{train}(\theta )=\frac{1}{m}\sum_{i=1}^{m}cost(\theta ,(x^{(i)},y^{(i)}))$ ，其实和之前一样，就是变了一个形式而已。对于随机梯度算法，我们首先要做的一个工作就是把所有数据进行随机排序，这样在后面更新 $\theta _{j}$ 时可以让算法更快收敛，在这里我们对 $\theta _{j}$ 的更新算法是这样的：

Repeat{

for i=1,...,m{

$\theta _{j}:=\theta _{j}-\alpha (h_{\theta }(x^{(i)})-y^{(i)})x_{j}^{(i)}$ (for j=0,...,n)

}

以上就是这个算法的核心，对于 $(h_{\theta }(x^{(i)})-y^{(i)})x_{j}^{(i)}$ 在这里我们不是对整个J( $\theta$ )求导，而是对 $cost(\theta ,(x^{(i)},y^{(i)}))$ 求导，我们没有了求和运算，而对每一个 $\theta _{j}$ 就当前的数据进行一次更新，这样对于每个数据我们就可以更新一次所有 $\theta$ ，虽然在收敛时会比较曲折，而且最后结果一般情况是收敛到最小值的附近徘徊，不会像批量梯度算法那样每一次更新完都使算法更加收敛并以接近直线的方式收敛到最小值，但这样少了大量的计算量，整体速度会提高不少，所以最后的结果我们是可以接受的。

15.3 小批量梯度下降法

在前面，我们给大家介绍了随机梯度下降算法是如何让整体速度提高的，在这一节给大家介绍一个新的梯度下降算法：小批量梯度下降法，它可以说是介于两者之间的算法，但计算的速度有时比随机梯度下降算法更快。对于批量梯度算法，我们在更新 $\theta _{j}$ 时，用了m组数据，而随机梯度下降算法是用1组数据，而我们的小批量梯度算法是使用b组数据，b可以为10，一般在2~100之间。假设我们有m=1000，b=10，这个时候我们的更新算法就是：

Repeat{

for i=1,11,21,31,...,991{

$\theta _{j}:=\theta _{j}-\alpha \frac{1}{10}\sum_{k=i}^{i+9}(h_{\theta }(x^{(k)})-y^{(k)})x_{j}^{(k)}$ (for j=0,...,n)

}

对于小批量梯度下降算法，我们每次计算b组数据，我们在计算那个b组求和时，我们可以通过向量化来计算，这样就更快了。

15.4 随机梯度下降法的收敛

关于随机梯度下降法，我们对于每一步的更新 $\theta _{j}$ ，我们不清楚我们的算法是否收敛了，所以在更新下次的 $\theta _{j}$ 之前，我们需要计算 $cost(\theta ,(x^{(i)},y^{(i)}))$ ，我们可以画出 $cost(\theta ,(x^{(i)},y^{(i)}))$ 的图像来判断整体是否在收敛。如图4所示，由于随机梯度下降法是根据每一个数据就会更新，所以不是那么平滑，但可以看出整体是下降的，这个时候的 $\alpha$ 比较小，如果我们使 $\alpha$ 更小一点，会发现最后下降的结果更小，但是区别不大，所以在很多时候，如果我们发现整体是在收敛的，我们就会固定 $\alpha$ 不变，因为不断改变 $\alpha$ 意义不是很大，就算最后结果是一个局部最小值，我们也可以接受。

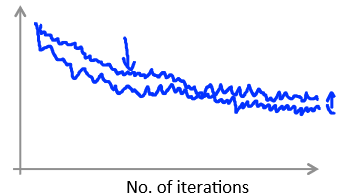
图4 当 $\alpha$ 较小时

当数据更多时，比如从m=1000增加到m=5000，如图5所示，我们会发现更平滑了一些，表示收敛时更快了。

图5 当m更大时

但如果我们发现我们的曲线是在慢慢增长的，如图6所示，则表示我们的 $\alpha$ 选大了，我们需要减小 $\alpha$ 。

图6 曲线是增长的

关于学习速率 $\alpha$ ，我们一般是选定一个较小的值，使得整体是在收敛的，就固定不变，但这样的结果是最终的算法不会收敛到一个最小的值，所以如果想收敛到一个最小的值，则我们需要不断地更新 $\alpha$ ，即减小 $\alpha$ ，我们有一个方法是让 $\alpha =\frac{const1}{iterationNumber+const2}$ ，因为迭代次数是不断增加的，所以 $\alpha$ 不断在减小，但是这个式子中有两个常数，我们需要去确定，所以还是比较麻烦，通常也不会这样做，还是得看自己实际的需要吧。

15.5 在线学习问题

在前面给大家介绍了随机梯度算法和小批量梯度算法，在这里给大家介绍下在线学习算法，也是他们的一些变种，这个算法在每次处理数据时也是每次处理一组数据，在我们的实际中也用到很多。比如你在网上有一个网店是卖手机的，店里有100种手机，当有顾客需要买手机时在搜索栏进行搜索自己想要手机的特征，我们相应地进行推荐，使顾客尽可能地会去点击每个商品，即尽可能的都是他想要的商品，我们用y=1表示用户对此商品进行了点击，用y=0表示用户没有对此商品进行点击，用 $p(y=1|x;\theta )$ 来表示此商品可能被点击的概率，我们就是要对此进行学习，这样才能推荐相应点击率高的商品给顾客。这就是一个在线学习的例子，我们对每个用户进行学习，这里的用户数据就像一条流水线一样，是源源不断的，所以我们每次都是对当前用户进行学习更新，然后就扔掉当前的数据，进行下一个数据的学习。

还有一些例子，比如推荐文章的例子，也是根据你的点击率来进行学习，然后推荐相应的文章给你，还有网上买书例子等等，都是在线学习问题。

15.6 映射约减和数据的并行

在前面介绍的随机梯度下降法，小批量梯度下降法还有他们的一些变种算法都是只能在一台计算机上运行，但当有很多的数据时，我们不希望只在一台计算机上运行，而希望有几台计算机共同合作完成。这就是Map-reduce(映射约减)算法，对于这个算法和随机梯度下降算法哪个更好，并没有一个明确的答案，各有各的好，只能根据实际要求和条件来进行选择。

假设我们现在有400组数据，即m=400，对于批量梯度下降法的每次更新 $\theta _{j}:=\theta _{j}-\alpha \frac{1}{400}\sum_{i=1}^{400}(h_{\theta }(x^{(i)})-y^{(i)})x_{j}^{(i)}$ ，前面我们也说了这样的计算量很大，但是如果我们现在有4台计算机，我们可以把数据分成4份，即

Machine 1:Use $(x^{(1)},y^{(1)}),(x^{(2)},y^{(2)}),...,(x^{(100)},y^{(100)})$

$temp_{j}^{(1)}=\sum_{i=1}^{100}(h_{\theta }(x^{(i)})-y^{(i)})x_{j}^{(i)}$

Machine 2:Use $(x^{(101)},y^{(101)}),(x^{(102)},y^{(102)}),...,(x^{(200)},y^{(200)})$

$temp_{j}^{(2)}=\sum_{i=101}^{200}(h_{\theta }(x^{(i)})-y^{(i)})x_{j}^{(i)}$

Machine 3:Use $(x^{(201)},y^{(201)}),(x^{(202)},y^{(202)}),...,(x^{(300)},y^{(300)})$

$temp_{j}^{(3)}=\sum_{i=201}^{300}(h_{\theta }(x^{(i)})-y^{(i)})x_{j}^{(i)}$

Machine 4:Use $(x^{(301)},y^{(301)}),(x^{(302)},y^{(302)}),...,(x^{(400)},y^{(400)})$

$temp_{j}^{(4)}=\sum_{i=301}^{400}(h_{\theta }(x^{(i)})-y^{(i)})x_{j}^{(i)}$

最后再进行整合： $\theta _{j}:=\theta _{j}-\alpha \frac{1}{400}(temp_{j}^{(1)}+temp_{j}^{(2)}+temp_{j}^{(3)}+temp_{j}^{(4)})$ (for j=0,...,n)

以上即是整个算法实现的过程，我们就会感觉多组数据一起并行运算，如图7所示，是映射约减过程的示意图，对于逻辑回归，这个也是同样适用的，按道理讲，这样做，我们整体的速度会提高四倍，但是由于整合时一些延缓，我们最终提高的速度会小于四倍的速度。

图7 Map-reduce

如果我们没有多台计算机，是不是就不能进行映射约减了？不是的，现在计算机一般都是多核的，如图8所示，我们就可以把分好的数据放在每个内核上进行计算，最后再整合。

图8 多核计算机

Large scale machine learning(大规模机器学习)

前言

猜你喜欢