线性判别分析（LDA）与主成分分析（PCA）

简介

线性判别分析（LDA）

1. 什么是LDA

线性判别分析（Linear Discriminant Analysis，LDA）是一种经典的降维方法。LDA是一种监督学习的降维技术，数据集的每个样本有类别输出。

2. LDA的特点

• 多维空间中，数据处理分类问题较为复杂，LDA算法将多维空间中的数据投影到一条直线上，将d维数据转化成1维数据进行处理。
• 对于训练数据，设法将多维数据投影到一条直线上，同类数据的投影点尽可能接近，异类数据点尽可能远离。
• 对数据进行分类时，将其投影到同样的这条直线上，再根据投影点的位置来确定样本的类别（找到更合适分类的空间）。 如果用一句话概括LDA思想，即“投影后类内方差最小，类间方差最大”。 （与PCA不同，更关心分类而不是方差）

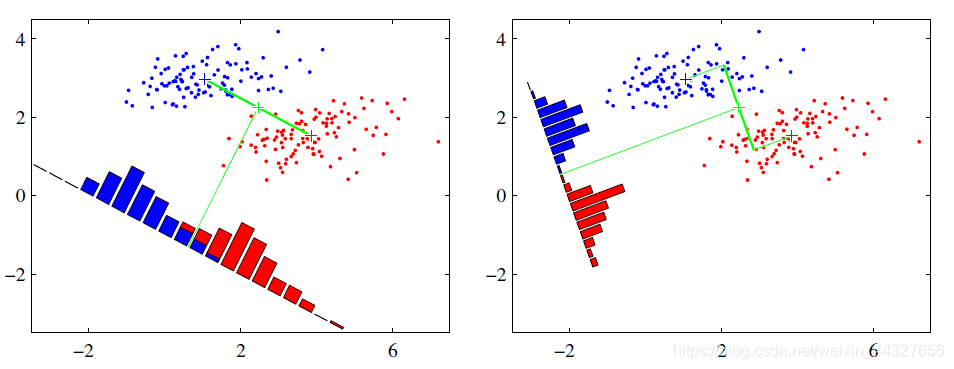
3. LDA的核心思想
   
   左图：让不同类别的平均点距离最远的投影方式 ， 右图：让同类别的数据挨得最近的投影方式。

   从上图直观看出，右图红色数据和蓝色数据在各自的区域来说相对集中，根据数据分布直方图也可看出，所以右图的投影效果好于左图，左图中间直方图部分有明显交集。
   ​ 以上例子是基于数据是二维的，分类后的投影是一条直线。如果原始数据是多维的，则投影后的分类面是一低维的超平面。

4. LDA算法原理
   输入：数据集 $D={(x_1,y_1),(x_2,y_2),...,(x_m,y_m)}​$，其中样本 $x_i ​$ 是n维向量， $y_i \epsilon {C_1, C_2, ..., C_k}​$，降维后的目标维度 $d​$。定义

   ​ $N_j(j=0,1)$ 为第 $j$ 类样本个数；

   ​ $X_j(j=0,1)$ 为第 $j$ 类样本的集合；

   ​ $u_j(j=0,1)​$ 为第 $j​$ 类样本的均值向量；

   ​ $\sum_j(j=0,1)$ 为第 $j$ 类样本的协方差矩阵。

   其中 $u_j = \frac{1}{N_j} \sum_{x\epsilon X_j}x(j=0,1)， \sum_j = \sum_{x\epsilon X_j}(x-u_j)(x-u_j)^T(j=0,1)$ ​ 假设投影直线是向量 $w$，对任意样本 $x_i$，它在直线 $w$上的投影为 $w^tx_i$，两个类别的中心点 $u_0$, $u_1 $在直线 $w$ 的投影分别为 $w^Tu_0$ 、 $w^Tu_1$。

   ​ LDA的目标是让两类别的数据中心间的距离 $| w^Tu_0 - w^Tu_1 |^2_2$ 尽量大，与此同时，希望同类样本投影点的协方差 $w^T \sum_0 w$、 $w^T \sum_1 w$ 尽量小，最小化 $w^T \sum_0 w - w^T \sum_1 w​$ 。 ​ 定义 ​ 类内散度矩阵 $S_w = \sum_0 + \sum_1 = \sum_{x\epsilon X_0}(x-u_0)(x-u_0)^T + \sum_{x\epsilon X_1}(x-u_1)(x-u_1)^T$ ​ 类间散度矩阵 $S_b = (u_0 - u_1)(u_0 - u_1)^T$

   ​ 据上分析，优化目标为 $\arg \max J(w) = \frac{| w^Tu_0 - w^Tu_1 |^2_2}{w^T \sum_0w + w^T \sum_1w} = \frac{w^T(u_0-u_1)(u_0-u_1)^Tw}{w^T(\sum_0 + \sum_1)w} = \frac{w^TS_bw}{w^TS_ww}$ ​ 根据广义瑞利商的性质，矩阵 $S^{-1}{w} S_b$ 的最大特征值为 $j(w)$ 的最大值，矩阵 $S^{-1}{w} S_b$ 的最大特征值对应的特征向量即为 $w​$。

5. LDA算法降维流程
   输入：数据集 $D = { (x_1,y_1),(x_2,y_2), ... ,(x_m,y_m) }$，其中样本 $x_i $ 是n维向量， $y_i \epsilon {C_1, C_2, ..., C_k}$，降维后的目标维度 $d$ 。
   输出：降维后的数据集 $\overline{D} $ 。

   步骤：

   • 计算类内散度矩阵 $S_w$。
   • 计算类间散度矩阵 $S_b​$ 。
   • 计算矩阵 $S^{-1}_wS_b​$ 。
   • 计算矩阵 $S^{-1}_wS_b$ 的最大的 d 个特征值。
   • 计算 d 个特征值对应的 d 个特征向量，记投影矩阵为 W 。
   • 转化样本集的每个样本，得到新样本 $P_i = W^Tx_i​$ 。
   • 输出新样本集 $\overline{D} = { (p_1,y_1),(p_2,y_2),...,(p_m,y_m) }​$

6. LDA的优缺点

   优点	缺点
   1.可以使用类别的先验知识，2. 以标签、类别衡量差异性的有监督降维方式，相对于PCA的模糊性，其目的更明确，更能反映样本间的差异；	1. LDA不适合对非高斯分布样本进行降维；2. LDA降维最多降到k-1维；3. LDA在样本分类信息依赖方差而不是均值时，降维效果不好；4. LDA可能过度拟合数据。

主成分分析（PCA）

1. 什么是PCA
   PCA就是将高维的数据通过线性变换投影到低维空间上去，投影思想是找出最能够代表原始数据的投影方法。被PCA降掉的那些维度只能是那些噪声或是冗余的数据。去冗余的目的是去除可以被其他向量代表的线性相关向量，因为这部分信息量是多余的。去噪声的目的去除较小特征值对应的特征向量，特征值的大小反映了变换后在特征向量方向上变换的幅度，幅度越大，说明这个方向上的元素差异也越大，要保留。

2. PCA的特点
   PCA可解决训练数据中存在数据特征过多或特征累赘的问题。核心思想是将m维特征映射到n维（n < m），这n维形成主元，是重构出来最能代表原始数据的正交特征
   
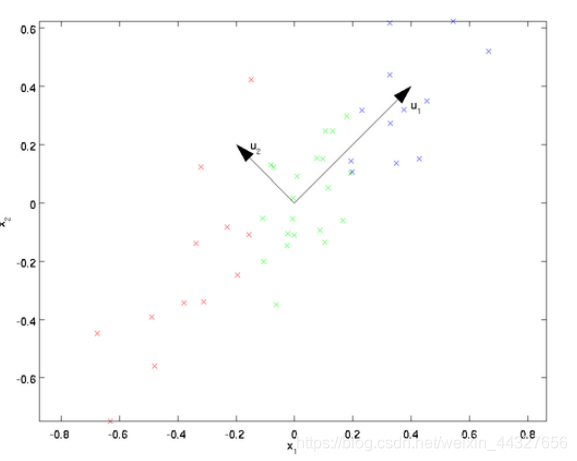
   从图可看出， $u_1$比 $u_2$好，为什么呢？有以下两个主要评价指标：
   1) 样本点到这个直线的距离足够近。
   2)样本点在这个直线上的投影能尽可能的分开。
   如果我们需要降维的目标维数是其他任意维，则：
   1)样本点到这个超平面的距离足够近。
   2)样本点在这个超平面上的投影能尽可能的分开。

3. PCA的核心思想

4. PCA算法流程
   输入： $n​$ 维样本集 $D = \left( x^{(1)},x^{(2)},...,x^{(m)} \right)​$ ，目标降维的维数 $n&#x27;​$ 。
   输出：降维后的新样本集 $D&#x27; = \left( z^{(1)},z^{(2)},...,z^{(m)} \right)$ 。
   主要步骤如下：

   1. 对所有的样本进行中心化，$ x^{(i)} = x^{(i)} - \frac{1}{m} \sum^m_{j=1} x^{(j)} $ 。
   2. 计算样本的协方差矩阵 $XX^T​$ 。
   3. 对协方差矩阵 $XX^T$ 进行特征值分解。
   4. 取出最大的 $n’ $ 个特征值对应的特征向量 ${ w_1,w_2,...,w_{n&#x27;} }$ 。
   5. 标准化特征向量，得到特征向量矩阵 $W$ 。
   6. 转化样本集中的每个样本 $z^{(i)} = W^T x^{(i)}$ 。
   7. 得到输出矩阵 $D&#x27; = \left( z^{(1)},z^{(2)},...,z^{(n)} \right)​$ 。 注：在降维时，有时不明确目标维数，而是指定降维到的主成分比重阈值 $k(k \epsilon(0,1])​$ 。假设 $n​$ 个特征值为 $\lambda_1 \geq \lambda_2 \geq ... \geq \lambda_n​$ ，则 $n&#x27;​$ 可从 $\sum^{n&#x27;}{i=1} \lambda_i \geq k \times \sum^n{i=1} \lambda_i ​$ 得到。

5. PCA算法主要优缺点

优点	缺点
1.仅仅需要以方差衡量信息量，不受数据集以外的因素影响，2.各主成分之间正交，可消除原始数据成分间的相互影响的因素。3. 计算方法简单，主要运算是特征值分解，易于实现。	1.主成分各个特征维度的含义具有一定的模糊性，不如原始样本特征的解释性强。2. 方差小的非主成分也可能含有对样本差异的重要信息，因降维丢弃可能对后续数据处理有影响。

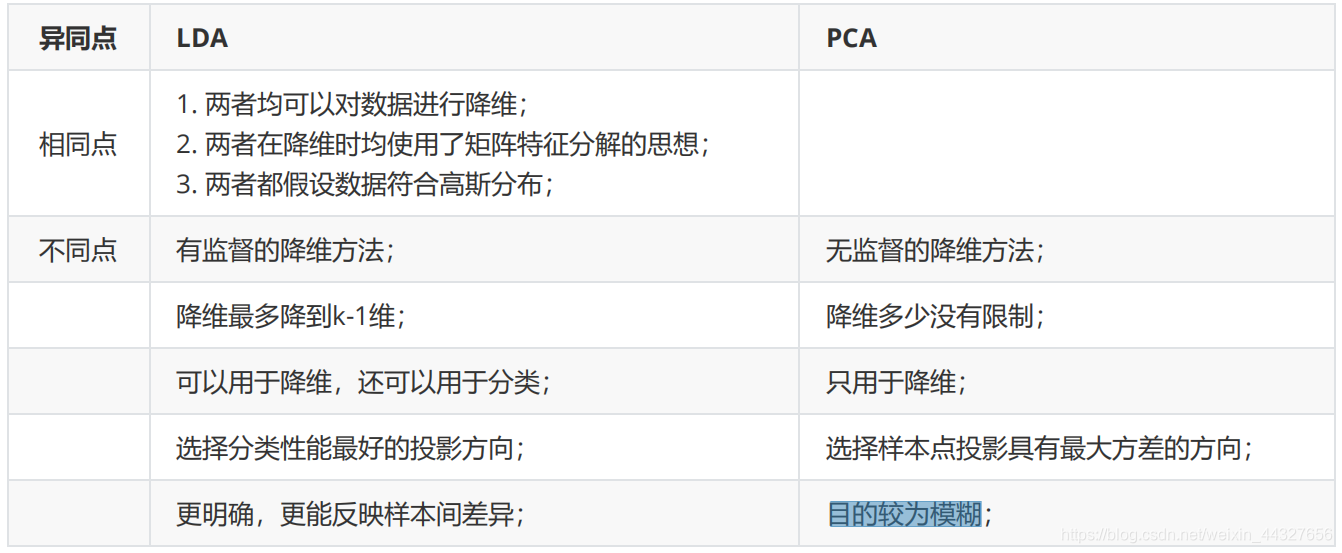
LDA和PCA的异同点